FÍSICA - aula 2

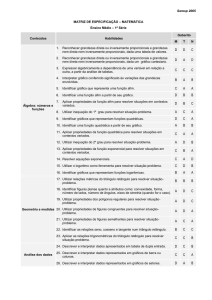
Física
Aula 02 - Mecânica
Prof.: Célio Normando
Assunto:
Relações entre as grandezas
- Grandezas diretamente
proporcionais
-Grandezas inversamente
proporcionais
-Grandezas que variam linearmente
Prof.: Célio Normando
Introdução
Na Física, geralmente, a variação de uma grandeza
implica na variação de outra.
Y
10 15
22
22
34
X
0
5
6
8
2
X (varia)  Y (varia)
Quando isto ocorre, afirma-se que estas grandezas são
variáveis dependentes.
Y e X são grandezas dependentes
Introdução
Se, no entanto, uma grandeza varia e a outra
permanece constante:
V
10
10
10
10
10
t
1
3
5
7
9
Diz-se que V e t são grandezas independentes
Assim, Se t (varia) e V (permanece constante)
V e t são variáveis independentes
tem-se :
Introdução
Observe as grandezas S e t na tabela abaixo:
S
10 16
22
28
34
t
0
4
6
8
2
Como S depende de t? São grandezas diretamente proporcionais ou
inversamente proporcionais?
Se a razão entre seus valores for constante, elas são diretamente
proporcionais. Se o produto de seus valores for constante são
inversamente proporcionais.
Neste caso, elas não são nem diretamente e nem inversamente
proporcionais.
E então, como variam? Observe as tabelas seguintes e você mesmo
poderá responder no final desta aula.
Grandezas diretamente
proporcionais
Verifique a tabela seguinte:
Y
X
8
16
24
32
40
1
2
3
4
5
Como a grandeza Y se
relaciona com a X?
Y é diretamente proporcional a X, pois a razão entre seus valores
é constante
Y/X =K (Constante) => Y=KX
FUNÇÃO LINEAR
Grandezas diretamente
proporcionais
Quando duas grandezas são diretamente proporcionais,
como fica o gráfico de uma contra a outra?
Y
X
8
16 24 32
40
1
2
5
3
4
Y
Reta passando pela origem
40
32
24
16
8
0
1 2 3 4 5
X
Grandezas diretamente
proporcionais
Algumas grandezas físicas são diretamente proporcionais.
A força elástica (f) e a deformação (x) são diretamente
proporcionais?
f(N)
0
x(cm)
0
20
40
60
80
0,25 0,50 0,75 1,00
Sim, pois a razão entre f e x é uma constante (k) ou seja:
f=kx
k: constante elástica da mola
Grandezas diretamente
proporcionais
O gráfico da força elástica (f) versus a deformação (x)
f(N)
0
x(cm)
0
20
40
60
80
0,25 0,50 0,75 1,00
f
(N)
80
60
40
20
0
0,25 0,50 0,75 1,00
x (cm)
Grandezas diretamente
proporcionais
A tensão (U) e a intensidade de corrente elétrica (i) são
grandezas diretamente proporcionais para os condutores
ôhmicos.
Veja a expressão matemática que traduz a lei física (Lei
de OHM)
U = R (Constante)
i
U = R i (Lei de OHM)
Grandezas inversamente
proporcionais
Nesta nova tabela as grandezas Y e X têm um
comportamento diferente.
Y
30 15 10 7,5
6
X
1
5
2
3
4
Como a grandeza Y se
relaciona com a X?
Y é Inversamente proporcional a X, pois o produto Y . X é
constante
Y . X = K (constante) => Y = K / X
FUNÇÃO RECÍPROCA
Grandezas inversamente
proporcionais
Como Y é inversamente proporcional a X o gráfico de Y
contra X é uma curva. Veja a construção do gráfico.
Y
30
15
10 7,5
6
Y
30
X
1
2
3
4
5
Esta curva é denominada
Hipérbole Eqüilátera.
15
10
7,5
6
0
1 2 3 4 5
X
Grandezas inversamente
proporcionais
Você conhece estas grandezas físicas?
f= 1
T
f: é a freqüência
T: é o período
A freqüência (f) e o período (T) são inversamente
proporcionais pois o produto f . T = 1 (constante).
Grandezas inversamente
proporcionais
Agora observe como a velocidade (v) da luz varia com
o índice de refração (n) do meio onde ela se propaga.
V
(108 m/s)
3
Será que você pode concluir que v e n
são
grandezas
inversamente
proporcionais?
Que tal verificar o produto de v . n.
Note que: v1 . n1 = v2 . n2
2
0
1
1,5
n
3 x 108 x 1 = 2 x 108 x 1,5
Grandezas inversamente
proporcionais
O produto é constante e vale 3 x 108 m/s, que chamaremos
de c.
Desta forma é constante v . n = c (a curva é uma hipérbole
eqüilátera).
O índice de refração (n) é inversamente proporcional a
velocidade de propagação da luz.
c
n=
v
Grandezas que variam
linearmente
A tabela abaixo mostra o comportamento de duas
grandezas.
Y
20
40 60 80 100
X
0
5
10
15
20
E agora, como Y e X se
relacionam?
Y varia linearmente com X, pois para variações iguais de X tem-se
correspondentes variações iguais em Y.
Relação Matemática
Y = aX + b
Função AFIM ou Função do 1o Grau
Grandezas que variam
linearmente
Y = aX + b
Y
a = X (Coeficiente angular)
b = Y quando X = 0 (Coeficiente linear)
Y
Y
20
40 60 80 100
X
0
5
a = 40 - 20
5-0
10
15
a=4
X = 0 Y = 20
Então b = 20.
20
100
80
60
40
20
a>0
0 5 10 15 20 X
Reta crescente que não passa pela
origem.
Grandezas que variam
linearmente
Caso o coeficiente angular (a) seja menor que zero (a<0)
veja como fica o gráfico:
Y
a<0
0
X
Reta decrescente que não passa pela origem
Grandezas que variam
linearmente
Está lembrando das grandezas S e t do início desta aula.
S(m) 10
t (s)
0
16
22
28
34
2
4
6
8
Elas nem eram diretamente proporcionais e nem inversamente
proporcionais.
Observe que para variações iguais de tempo (t) de (2 em 2s)
têm-se variações iguais da posição (s) de (6 em 6m)
A posição (S) varia linearmente com o tempo (t) no movimento
uniforme.
S = So + vt
Agora procure resolver as
Atividades para Sala e
Atividades Propostas.
As soluções estão
disponíveis no Click Professor.