0 - if - ufrgs

Por que acontecem efeitos não lineares?
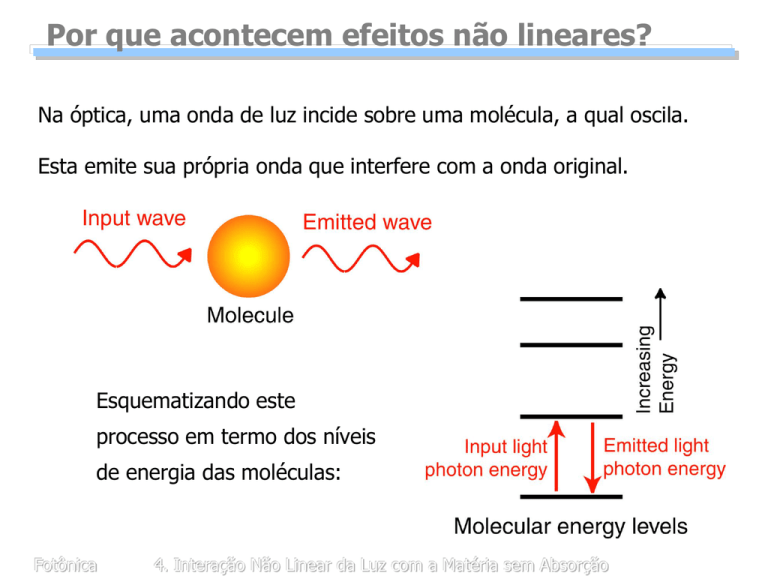
Na óptica, uma onda de luz incide sobre uma molécula, a qual oscila.
Esta emite sua própria onda que interfere com a onda original.
Esquematizando este
processo em termo dos níveis
de energia das moléculas:
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Por que acontecem efeitos não lineares?
Agora, suponha que intensidade é alta o bastante para excitar as
moléculas para um estado de alta energia. Esse estado pode se tornar
o nível inferior de uma excitação.
Esta gera vibrações em todas as freqüências correspondentes a todas
diferenças de energia entre estados ocupados.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Óptica não linear é análoga à eletrônica não linear
Enviando um único sinal harmônico (“freqüência pura”) para um
alto-falante barato, resulta em um sinal de saída truncado, mais
parecido com uma onda quadrada. Observando o espectro de
freqüencias, observamos um novo conjunto dessas.
O que ouvimos é distorção.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Óptica não linear e osciladores não harmônicos
Olhando para o dipolo gerador da nova onda, a não linearidade óptica é
visualizada através do potencial eletrônico, quando esse deixa de ser um
simples potencial harmônico.
Exemplo: o movimento vibracional em uma molécula:
Para campos fracos, o movimento é harmônico, prevalecendo o regime e
fenômenos de óptica linear.
Para campos fortes (lasers), ocorre o movimento não harmônico, e outros
harmônicos surgem, tanto no movimento, quanto na emissão de luz.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Equações de Maxwell em um Meio Material
A polarização induzida, P, contém o efeito do meio:
 E  0
 B  0
B
 E  
t
1 E
P
 B  2
 0
c0 t
t
Estas equações podem ser reduzidas à equação de onda escalar:
 2E 1  2E
 2
2
z
c0 t 2
 2P
 0
t 2
“Equação de Onda
não homogênea”
Soluções harmônicas;
a polarização impõe a freqüência de oscilação (a fonte).
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Polarização Linear
Para baixas intensidades escrevemos:
P   0 E
Desta forma, obtemos:
 2E 1  2E
 2
2
z
c0 t 2
Simplificando:
 2E 1    2E
 2
2
z
c0 t 2
Com a seguinte solução:
onde
1  2E
 2 2
c0
t
 = ck
Utilizando o fato que:
 0 0  1/ c02
 0
E ( z , t )  E0 cos( t  k z )
and c = c0 /n and
n = (1+)1/2
A polarização induzida apenas modifica o índice de refração.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Equações de Maxwell em um Meio Não Linear
A óptica não linear surge quando a polarização é resultante
de termos de alta ordem (não lineares!) no campo:
(1)
(2)
2
(3)
3

E



E


E


E
 ...
P
0 
Quais são os efeitos dos termos não-lineares? Considere o
segundo termo:
Since E (t )  E exp(i t )  E exp(i t ),
*
E (t )  E exp(2i t )  2 E  E *2 exp(2i t )
2
2
2
2 = 2o harmônico!
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Geração de soma e de diferença de freqüências
Suponha que dois feixes de cores estão presentes:
E (t )  E1 exp(i1t )  E1* exp(i1t )  E2 exp(i2t )  E2* exp(i2t )
Então:
E (t )2  E12 exp(2i1t )  E1*2 exp(2i1t )
SHG
 E22 exp(2i 2t )  E2*2 exp(2i 2t )
SHG
 2 E1E2 exp(i 1   2  t )  2 E1* E2* exp(i 1   2  t )
SFG
 2 E1E2 exp(i 1   2  t )  2 E1* E2* exp(i 1   2  t )
DFG
 2 E1  2 E2
2
Fotônica
2
dc retificação
4. Interação Não Linear da Luz com a Matéria sem Absorção
Efeitos não-lineares complicados podem ocorrer
Processos ópticos não lineares são
usualmente denominados:
“Processos de mistura de N-ondas"
onde N é o número de fótons
envolvido (inclusive o emitido).
Freqüência da luz emitida
Quanto mais fótons (i.e., maior a ordem) porém mais fraco o efeito.
Efeitos de ordem muito alta podem ser observados, mas esses
requerem alta intensidade. Ainda, se as energias dos fótons
coincidem com uma ressonância do meio, o efeito é amplificado.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Polarização Induzida para efeitos não lineares
Setas apontando para cima
correspondem a absorção de fótons
e contribuem com um fator de
campo, Ei;
Setas apontando para baixo
correspondem à emissão de fótons
e contribuem com um fator de
complexo conjugado do campo:
P   0  (5) E1 E2 E3 E4* E5
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Resolvendo a equação de onda para ONL
 2E 1  2E
 2
2
z
c t 2
 2P
 0
t 2
Levando em conta a
polarização linear e
trocando c0 por c.
O campo total E contém muitas freqüências discretas, 1, 2, etc.
Escrevendo separadamente as equações de onda para cada freqüência,
considerando apenas a polarização induzida nesta freqüência:
 2E1 1  2E1
 2
2
z
c t 2
 2P1
 0 2
t
E1 e P1 são os campos elétrico e
polarização na freqüência 1.
 2E2 1  2E2
 2
2
z
c t 2
 2P2
 0
t 2
e E2 e P2 são os campos elétrico
e polarização na freqüência 2.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Aproximação de Envelope Lentamente Variável
Escrevendo o pulso do campo elétrico como o produto de um envelope
e uma exponencial complexa:
E0(z,t) = E0 (z,t) exp[i(0 t – k0 z)]
Neste caso, consideramos ainda que o envelope do novo pulso não se
altera rapidamente.
Esta é a Aproximação de Envelope Lentamente Variável.
Se d é a escala de comprimento de variçào do envelope, esta
aproximação resulta na condição: d >> l
E0
E0
E0
~
 2
 k0 E0
z
d
l
 2 E0
E0 / z
E0 / z
E0
~
 2
 k0
2
z
d
l0
z
Comparndo E0 e suas derivadas:
Fotônica
 2 E0
E0
2

k

k
0
0 E0
2
z
z
4. Interação Não Linear da Luz com a Matéria sem Absorção
Aproximação de Envelope Lentamente Variável
Fazendo o mesmo no tempo:
Se t é a escala de tempo da variação do envelope : t >> T0
onde T0 correponde ao período de um ciclo óptico, 2/0.
E0
E
E
~ 0  2 0  0 E0
t
t
T0
 2 E0
E0 / t
E0 / t
E0
~
 2
 0
2
t
t
T0
t
Comparando E0 e suas derivadas temporais:
 2 E0
E0
2




0
0 E0
2
t
t
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Aproximação de Envelope Lentamente Variável
Repetindo todo o procedimento para a polarização:
P (z,t) = P0 (z,t) exp[i(0 t – k0 z)]
Se t é a escala de tempo da variação do envelope : t >> T0
onde T0 correponde ao período de um ciclo óptico, 2/0.
P0
P
P
~ 0  2 0  0 P0
t
t
T0
 2 P0
P0 / t
P0 / t
P0
~
 2
 0
2
t
t
T0
t
Comparando P0 e suas derivadas temporais:
Fotônica
 2 P0
P0
2




0
0 P0
2
t
t
4. Interação Não Linear da Luz com a Matéria sem Absorção
Aproximação de Envelope Lentamente Variável
Calculando as derivadas:
E0  E0


 ik0 E0  exp[i (0 t  k0 z )]
z
 z


E0
 2E0   2 E0
2
  2  2ik0
 k0 E0  exp[i(0t  k0 z )]
2
z
z
 z

x
x
x x

E0
 2E0   2 E0
2
  2  2i0
 0 E0  exp[i(0t  k0 z )]
2
t
t
 t


P0
 2P0   2 P0
2
  2  2i0
 0 P0  exp[i(0t  k0 z )]
2
t
t
 t

Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Aproximação de Envelope Lentamente Variável
Substituindo os sobreviventes na equação para 0:
 2E0 1  2E0
 2
2
z
c t 2
 2P0
 0
t 2

E0 2i 0 E0
0 2 
2
2

2
ik


k
E

E
exp[
i
(

t

k
z
)]





0
0
0
0
0
0
0 0 P0 exp[i ( 0 t  k 0 z )]
2
2
z
c
t
c


xx
Como k0 = 0 / c, os dois útimos termos entre colchetes cancelam-se.
2ik0
E0 2i0 E0
2
 2
 00 P0
z
c
t
Dividindo por 2ik0:
E0 1 E0
 0 0

 i
P0
z c t
2k0
2
Fotônica
Aproximação de Envelope
Lentamente Variável
4. Interação Não Linear da Luz com a Matéria sem Absorção
Incluindo dispersão
Realizando a tranformada de Fourier, expandindo k()
em primeira ordem em , substitui-se c por vg:
E0 1 E0


  i 0 0 P0
z v g t
2k0
2
Dispersão de velodidade de grupo GVD em segunda ordem:
E0 1 E0 i d 2 k  2 E0
00




i
P0
2
2
z v g t 2 d t
2k0
2
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
No referencial do envelope (surfando)
No sistema de coordenadas:
zv = z
tv = t – z / vg
Transformando as derivadas:
E0
E0 zv E0 tv


z
zv z tv z
E0
E0
E0


z
zv
t v
E0
E0 zv E0 tv


t
zv t tv t
 1
 
 v g 
E0
E0
 0 
t
tv
SVEA torna-se:
E0
E0

zv
tv
x x
 1 1
  
 v g  v g
 E0 
 00 2
P0

  i
2k0
 tv 
Cancelam-se as
derivadas temporais!
Canceling terms, the SVEA becomes:
E0

  i 0 0 P0
zv
2k0
2
Fotônica
We’ll drop the subscript (v) to simplify
our equations.
4. Interação Não Linear da Luz com a Matéria sem Absorção
Vetores de onda de campos elétricos e polarizações
não são necessariamente iguais
Escolhemos 0 como soma das
incidentes ’s:
0  1  2  3  4  5
O vetor-k da luz nesta freqüência é:
k0  0 / c  0 n(0 ) / c0
O vetor-k da polarização induzida é:
k p  k1  k 2  k 3  k 4  k 5
Infelizmente, kp pode diferir de k0!
Nem sempre cancela-se exp(-ikz)’s…
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Casamento de fase
kp não ser o mesmo que k0 é efeito importante de casamento de fase.
Ele deve ser considera em todos os problemas de óptica não linear.
Se os k’s não casam, a polarização induzida e o campo elétrico
gerado se moverão dentro e fora de fase.
E0 ( z, t )  E0 ( z, t ) exp[i(0 t  k0 z)]
P0 ( z, t )  P0 ( z, t ) exp[i(0 t  kP z )]
E0

  i 0 0 P0 exp(i k z )
z
2k0
2
SVEA:
onde:
k  kP  k0
Integrando a SVEA ao longo do comprimento do meio (L) :
Fotônica
L
00
exp(i k z ) 
E0 ( L, t )   i
P0

2k0
i k
0
2
4. Interação Não Linear da Luz com a Matéria sem Absorção
Casamento de fase
E0 ( L, t )   i
00 2
2k0
 i
00 2
 i
002
 i
 00 2
 i
 00 2
2 k0
2k0
k0
k0
L
exp(i k z ) 
P0

i k
0
 exp(i k L)  1
P0 

i

k


 exp(i k L / 2)  exp(i k L / 2) 
P0 exp(i k L / 2) 

i

k


 exp(i k L / 2)  exp(i k L / 2) 
P0 exp(i k L / 2) 

2ik

 sin(k L / 2) 
P0 exp(i k L / 2) 

k

I
k small
Portanto:
E ( L, t )  sin(k L / 2) / k
k large
I ( L, t )  sin 2 (k L / 2) / k 2
L
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Dependência espacial senoidal da intensidade de SHG
Grande k
Pequeno k
Se k não é zero, a luz gerada em uma região está fora de fase com a
gerada em uma região posterior, causando cancelamento.
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Sinc2(kL/2)
Lembrando:
E0 ( L, t )   i
 00 2
k0
 sin(k L / 2) 
P0 exp(i k L / 2) 

k

Multiplicando e dividindo por L/2:
i
00 2
2k 0
 sin(k L / 2) 
P0 exp(i k L / 2) L 


kL
/
2


i
  c 0 0 P0 exp(i k L / 2) L sinc(k L / 2)
2
E0(L,t)  P0 L sinc (k L / 2)
2
I(L,t)  P0 L2 sinc2 (k L / 2)
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção
Sinc2(kL/2)
O campo:
E0
E0(L,t)  P0 L sinc (k L / 2)
k
A intensidade
2
I
I(L,t)  P0 L2 sinc2 (k L / 2)
k
Fotônica
Para maximizar a intensidade,
Temos que fazer k = 0. O
casamento de fase.
4. Interação Não Linear da Luz com a Matéria sem Absorção
Casamento de fase = Lei da conservação de fótons
Adicionando as freqüências:
1  2  3  4  5  0
É o mesmo que a conservação de energia
multiplicando-se por h cortado:
1  2  3  4  5  0
Somando os k’s conserva-se momentum:
k1  k 2  k 3  k 4  k 5  k 0
k1  k 2  k 3  k 4  k 5  k 0
Casamento de fase é equivalente às leis
de conservação de energia e momentum
Fotônica
4. Interação Não Linear da Luz com a Matéria sem Absorção