poligonos

Matemática Básica
Polígonos
É a figura que é formado por segmentos de reta
unidos por seus extremos dois a dois.
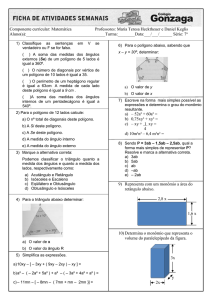
Vértice
Medida do
ângulo central
 B

Diagonal

A
 
 C

Centro
Medida do
ângulo externo

E 
 
D
Lado
Medida dol
ângulo interno
01- Polígono convexo - Las
medidas de seus ângulos
interiores são agudos.
03- Polígono equilátero - Seus
lados são congruentes.
02- Polígono cóncavo -La medida
de uno o mas de sus ángulos
interiores es cóncavo.
04- Polígono equiângulo - As medidas
de seus ângulos interiores são
congruentes.
05- Polígono regular - É equilátero e
por sua vez equiângulo.
Triângulo : 3 lados
Quadrilátero: 4 lados
Pentágono: 5 lados
Hexágono: 6 lados
Heptágono: 7 lados
Octógono: 8 lados
06- Polígono irregular - Seus lados
têm comprimentos diferentes.
Eneágono :
9 lados
Decágono:
10 lados
Unodecágono: 11 lados
Dodecágono: 12 lados
Pentadecágono:15 lados
Icoságono:
20 lados
PRIMEIRA PROPRIEDADE
Numericamente: Lados, vértices, ângulos interiores,
ângulos exteriores e ângulos centrais são iguais.
• Lados
• Vértices
• Ângulos interiores
• Ângulos exteriores
• Ângulos centrais
SEGUNDA PROPRIEDADE
A partir de um vértice de um polígono, se podem
traçar (n-3 ) diagonais.
Exemplo:
ND = (n-3) = (5-3) = 2 diagonais
TERCEIRA PROPRIEDADE
O número total de diagonais que se pode traçar em um polígono:
ND 
Exemplo:
ND 
n(n  3)
2
5(5  3)
 5 diagonais
2
QUARTA PROPRIEDADE
Ao traçar diagonais desde um mesmo vértice obtemos (n-2)
triângulos
Exemplo:
1
3
2
Ns. = ( n – 2 ) = 5 - 2 = 3 triângulos
QUINTA PROPRIEDADE
Soma das medidas dos ângulos interiores de un polígono:
Si =180°(n-2)
Donde (n - 2) é o número de triángulos
Exemplo:
Soma das medidas dos
ângulos interiores do triângulo
180º
180º
180º
Si = 180º x número de triângulos = 180º(5 - 2) = 540º
SEXTA PROPRIEDADE
Soma das medidas dos ângulos exteriores de um polígono é 360º
Se = 360°


Exemplo:



 +  +  +  +  = 360º
SÉTIMA PROPRIEDADE
Ao unir um ponto de um lado com os vértices opostos obtemos
(n - 1) triângulos
Exemplo:
Ponto qualquier de
um lado
4
1
3
2
Ns. = ( n – 1 ) = 5 - 1 = 4 triângulos
OITAVA PROPRIEDADE
Ao unir um ponto interior qualquier com os vértices obtemos
“n” triângulos
Exemplo:
5
4
1
3
2
Ns. = n = 5 = 6 triângulos
NONA PROPRIEDADE
Número de diagonais traçadas desde “V” vértices consecutivos, obtemos
com a siguinte fómula.
ND  nV 
Ejemplo:
( V  1)( V  2)
2
1
2
e assim
sucessivamente
1ª Propriedade
Medida de um ângulo interior de um
polígono
regular
ou
polígono
equiângulo.
m 
i
180(n  2)
n
3ª Propriedade
Medida de um ângulo central de um
polígono regular.
m c 
360
n
2ª Propriedade
Medida de um ângulo exterior de um
polígono
regular
ou
polígono
equiângulo.
m e 
360
n
4ª Propriedade
Soma das medidas dos ângulos
centrais.
Sc = 360°
Problema Nº 01
Em um polígono, a suma das medidas dos ângulos
exteriores e interiores és 1980°. Calcule o total de
diagonais deste polígono.
Do enunciado:
Se + Si = 1980°
Logo, substituindo pelas propriedades:
360° + 180°( n - 2 ) = 1980°
Resolvendo:
n = 11 lados
Número de diagonais:
n(n  3)
ND 
2
ND 
11 ( 11  3 )
2
ND = 44
Problema Nº 02
Como se denomina aquele polígono regular, no qual
a medida de cada um de seus ângulos internos é
igual a 8 vezes a medida de um ângulo externo.
Polígono é regular:
Do enunciado:
mi = 8(me )
Substituindo pelas propriedades:
180 ( n  2 )
360
 8 (
)
n
n
Resolvendo:
n = 18 lados
Logo polígono é regular se denomina:
Polígono de 18 lados
Problema Nº 03
Calcule o número de diagonais de um polígono
convexo, sabendo que o total das diagonais é
maior que seu número de lados em 75.
Do enunciado:
ND = n + 75
Substituindo a propriedade:
n(n3)
= n + 75
2
n2 - 5n - 150 = 0
Resolvendo:
n = 15 lados
Logo, o número total de diagonais:
n(n  3)
ND 
2
ND 
15 ( 15  3 )
2
ND = 90
Problema Nº 04
Em um polígono regular, um lado aumenta, a
medida de seu ângulo interno aumenta em 12°;
então o número de vértices do polígono é:
Polígono é regular:
Dol enunciado:
Polígono original: n lados
Polígono modificado: (n + 1) lados
Substituindo pela propriedade:
180( n  2 )
180( n  1  2 )
 12 
Resolvendo: n = 5 lados
n
n1
Número de lados = Número de vértices
NV= 5 vértices
Problema Nº 05
O número total de diagonais de um polígono regular
é igual ao triplo do número de vértices. Calcule a
medida de um ângulo central deste polígono.
Polígono é regular:
Do enunciado:
ND = 3n
Substituindo pela propriedade:
n(n3 )
= 3n
2
Resolvendo:
n = 9 lados
Logo, a medida de um ângulo central:
mc 
360
n
mc
360

9
mc = 40°