v - UFERSA

GRAFOS EULERIANOS E
HAMILTONIANOS
Prof. M.Sc. Fábio Francisco da Costa Fontes
Maio - 2009
Introdução



Caminhos que usam todos os vértices ou
todas as arestas de um grafo são geralmente
chamados de percursos
Uma grande variedade de problemas práticos
podem ser vistos como um percurso num
grafo
Eles se dividem em duas categorias:
Problemas do tipo euleriano
 Problemas do tipo hamiltoniano

Introdução



Problemas do tipo euleriano: requerem que
cada aresta seja percorrida pelo menos uma
vez
Problemas do tipo hamiltoniano: requerem
que cada vértice seja percorrido pelo menos
uma vez
Exemplos clássicos de otimização: o
problema do carteiro chinês e o problema do
caixeiro viajante
Introdução

Os dois problemas parecem ser semelhantes,
mas possuem complexidades bem diferentes
A maior parte dos problemas eulerianos são
resolvidos em tempo polinomial
 A maioria dos problemas hamiltonianos têm
uma solução de custo elevado e são
classificados como NP-difícil, é necessário a
utilização de técnicas aproximativas para se
obter um resultado em tempo hábil

Grafos Eulerianos



Um percurso euleriano é um percurso que
contém todos as arestas do grafo
Um circuito euleriano é um percurso
euleriano fechado
Um grafo euleriano é um grafo que contém
um circuito euleriano
u
t
v
z
w
y
x
Problemas Eulerianos

As pontes de Königsberg: é possível fazer um
percurso atravessando todas as pontes, sem
repetir nenhuma?
Problemas Eulerianos

Euler percebeu que só seria possível
atravessar o caminho inteiro passando uma
única vez em cada ponte se houvessem
exatamente dois pontos de onde saíssem um
número ímpar de caminhos.
Grafos Eulerianos

Em 1873, Hierholzer mostrou que um grafo
cujo todos os vértices têm grau par é
euleriano
Entrada:
Saída:
Um grafo conectado G cujos vértices têm grau par
Um circuito euleriano
Algoritmo: Circuito Euleriano
Inicie em qualquer vértice v
Construa um percurso fechado T em G
Enquanto existirem arestas de G fora do percurso T
Escolha qualquer vértice w em T, que seja incidente
a uma aresta fora do percurso
Iniciando em w, construa um percurso fechado D de
arestas fora do percurso T
Faça a união do percurso D em T no ponto w
Retorne T
Grafos Eulerianos

Exemplo:
w1
x
t2
y
t1
d1
t3
e1
v
z
d3
e2
t4
u
w
e3
w2
d2
Percursos Eulerianos

Algumas aplicações (e.g. as pontes de
Königsberg) requerem percursos eulerianos
abertos:


Um grafo conectado G tem um percurso
euleriano aberto se e somente se ele tem
exatamente dois vértices de grau ímpar
O uso do termo euleriano é idêntico para
dígrafos, exceto que os percursos são
direcionados
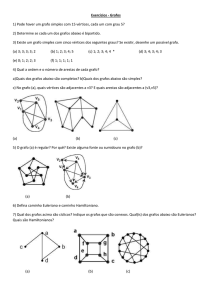
Exercícios

Determine qual dos grafos das famílias
abaixo são eulerianos:
O grafo completo Kn
 O grafo ciclo de n vértices Cn
 O grafo bipartido completo Km,n

Exercícios

Aplique o algoritmo para achar um circuito
euleriano (iniciando em s):
d
i
g
b
c
e
j
h
a
s
f
k
m
O Problema do Carteiro Chinês

O matemático chinês Meigu Guan introduziu
o problema em 1962:
Achar o caminho fechado mais curto que
percorra todas as arestas de um grafo pelo
menos uma vez
 É o problema do carteiro que quer entregar a
correspondência numa rede de ruas e retornar
ao escritório central o mais rápido possível

O Problema do Carteiro Chinês

Definição: um circuito do carteiro em um
grafo G é um caminho fechado que usa cada
aresta de G pelo menos uma vez

Definição: em um grafo com peso nas
arestas, um circuito ótimo do carteiro é um
circuito do carteiro cujo peso total das
arestas é mínimo
O Problema do Carteiro Chinês

Exemplo: achar o circuito ótimo do carteiro
no grafo abaixo:
a
6
3
b
7
c
2
d
3
e
5
f
6
5
4
6
g
h
10
i
5
O Problema do Carteiro Chinês



Edmonds e Johnson resolveram o problema
do carteiro chinês usando um algoritmo de
tempo polinomial
A idéia é duplicar arestas nos vértices de
grau ímpar, fazendo com que o grafo tenha
um circuito euleriano
O ponto chave do algoritmo é descobrir as
arestas de caminho mais curto entre os
vértices de grau ímpar
O Problema do Carteiro Chinês

Solução: duplicar arestas para os vértices de
grau ímpar e obter um circuito euleriano no
grafo
a
6
3
b
7
c
2
d
3
e
5
f
6
5
4
6
g
h
10
i
5
O Problema do Carteiro Chinês

O algoritmo de Edmonds e Johnson usa as
seguintes definições:

Definição: um casamento em um grafo G é um
subconjunto M de arestas de G tal que
nenhum par de arestas em M tem um ponto
final (vértice) em comum
y
a
b
g
M = {a,d}, {c,b}, {e,b}, ...
e
x
v
f
z
h
c
w
d
O Problema do Carteiro Chinês

O algoritmo de Edmonds e Johnson usa as
seguintes definições:

Definição: um casamento perfeito em um
grafo G é um casamento em que todo vértice
de G é um ponto final de uma das arestas de
M
a
M = {a,d}, {c,b}
y
b
x
z
c
w
d
O Problema do Carteiro Chinês
Entrada:
Saída:
Um grafo conectado G com peso nas arestas
Um circuito ótimo do carteiro W
Algoritmo: Circuito Ótimo do Carteiro
Ache o conjunto S de vértices com grau ímpar
Para cada par de vértices u e v em S
Ache duv, o caminho mais curto entre u e v
Forme um grafo completo K com os vértices em S
Para cada aresta e do grafo completo K
Atribua o peso duv para a aresta e=<u,v>
Ache um casamento perfeito M em K
cujo peso total das arestas é mínimo
Duplique as arestas de G correspondentes ao casamento M
Construa um circuito euleriano W no novo grafo G
W corresponde a um circuito ótimo do carteiro em G
Outros Problemas Eulerianos

Variações do problema do carteiro chinês
aparecem em diversas aplicações:
Coleta de lixo
 Limpeza das ruas
 Pintura de linhas no centro das ruas
 Patrulhamento da polícia
 Pesquisa de opinião e recenseamento
 Plotagem de uma rede

Grafos Hamiltonianos



Definição: um caminho hamiltoniano em um
grafo G é um caminho simples que contém
todos os vértices de G.
Definição: um ciclo hamiltoniano é um
caminho hamiltoniano fechado
Definição: um grafo hamiltoniano é um grafo
que tem um ciclo hamiltoniano
u
t
v
z
w
y
x
Grafos Hamiltonianos



Não existe uma regra simples (como para os
grafos eulerianos) para caracterizar um grafo
como hamiltoniano
O problema de saber se um grafo qualquer é
hamiltoniano é NP-completo
Um algoritmo de tempo polinomial para
resolver o problema não é conhecido
Grafos Hamiltonianos

Não existe um algoritmo que funcione para
qualquer grafo, mas:
Existem condições suficientes para um grafo
ser hamiltoniano que se aplicam a uma grande
classe de grafos
 Existem algumas regras básicas que ajudam a
identificar grafos que não são hamiltonianos

Grafos Não Hamiltonianos


As regras são baseadas na observação que
um ciclo hamiltoniano deve conter
exatamente duas arestas incidentes em cada
vértice
A estratégia para aplicar as regras é iniciar a
construção de um ciclo hamiltoniano e
mostrar que em algum ponto as regras se
contradizem
Grafos Não Hamiltonianos

Regras para grafos não-hamiltonianos:
 Se um vértice v tem grau 2, todas as arestas
incidentes em v devem fazer parte de
qualquer ciclo hamiltoniano
 Durante a construção, nenhum ciclo pode ser
formado até todos os vértices terem sido
visitados
 Se durante a construção, duas arestas
incidentes em um vértice v são necessárias,
todas as outras arestas incidentes podem ser
apagadas
Grafos Não Hamiltonianos

Exemplo:
v
Regra 1
h
Regra 2
Regra 3
a
b
f
g
e
c
d
w
x
Grafos Não Hamiltonianos

Exemplo
Regra 1
a
b
c
v
w
x
d
e
f
Regra 3
Grafos Hamiltonianos

Teorema (Ore, 1960): Seja G um grafo
simples de n vértices, onde n ≥ 3, tal que
deg(x) + deg(y) ≥ n para cada par de
vértices não adjacentes x e y. Então G é
hamiltoniano
v
w
x
y
u
Grafos Hamiltonianos

Corolário (Dirac 1952): Seja G um grafo
simples com n vértices, onde n ≥ 3, tal que
deg(v) ≥ n/2 para cada vértice v. Então G é
hamiltoniano
v
w
z
x
y
Grafos Hamiltonianos

Exercício: identifique se o grafo abaixo é ou
não hamiltoniano
u
t
v
z
w
y
x
Grafos Hamiltonianos

Exercício: identifique se o grafo abaixo é ou
não hamiltoniano
t
z
u
y
w
v
x
s
Grafos Hamiltonianos

Exercício: identifique se o grafo abaixo é ou
não hamiltoniano
t
z
u
y
w
v
x
s
O Problema do Caixeiro Viajante

O problema do caixeiro viajante consiste em
minimizar o custo de um caixeiro viajante
que deseja percorrer n cidades, visitando
cada cidade apenas uma vez, e retornar para
casa.
t
10
9
7
u
7
5
6
z
10
11
9
v
6
w
O Problema do Caixeiro Viajante

Dantzig, Fulkerson e Johnson foram os
primeiros a encontrar uma solução ótima
usando 49 cidades em 1954
Branch and Bound
 Cutting planes


Crowder e Padberg conseguiram uma
solução ótima para o problema usando 318
cidades em 1980
Branch and Bound
 Facet-defining inequalities

Heurísticas e Aproximações


Definição: uma heurística é um procedimento
que ajuda na tomada de uma decisão
quando existem múltiplas alternativas
Heurísticas são aplicadas quando é
impossível avaliar todas as possibilidades. É o
que faz, por exemplo, o jogador de xadrez
Heurísticas e Aproximações



Definição: um algoritmo heurístico é um
algoritmo cujos passos são guiados por uma
heurística.
Um algoritmo heurístico abdica da garantia
de achar a melhor solução, para que uma
solução possa ser encontrada rapidamente
A heurística mais simples para o caixeiro
viajante é a do vizinho mais próximo
Heurísticas e Aproximações

Segundo (BARR et al., 2001), Métodos
Heurísticos, também chamados algoritmos
aproximativos,
procedimentos
inexatos,
algoritmos incorretos, ou simplesmente
heurísticos são usados para identificar boas
soluções aproximadas para cada problema
em menos tempo que os algoritmos exatos
(quando este existir).
Heurísticas Construtivas
Heurísticas Construtivas
As Heurísticas de métodos construtivos
iniciam, sem nenhum resultado, a solução de
um problema e constroem passo a passo uma
solução viável. Apresentam algoritmos
gulosos, os quais, devido a enxergarem
apenas o que está mais próximo do objetivo
desejado, são também chamados de
algoritmos míopes.
Heurísticas Construtivas







Quando se trata de solucionar o PCV, as
variações desta classe de algoritmo, que se
apresentam com maior destaque, são:
o vizinho mais próximo;
a inserção mais próxima;
a inserção mais distante;
a inserção mais barata;
a inserção pelo maior ângulo;
o método das economias.
Heurísticas para o PCV
Entrada: um grafo completo com pesos nas arestas
Saída: uma seqüência de vértices que formam um ciclo hamiltoniano
Algoritmo: Vizinho mais próximo
Inicie em qualquer vértice v
rótulo(v) = 0
i = 0
Enquanto existirem vértices não rotulados
i = i + 1
Percorra a aresta de menor custo que une v a
um vértice não rotulado w
rótulo(w) = i
v = w
Heurísticas para o PCV


O algoritmo do vizinho mais próximo é rápido
e fácil de implementar
As vezes ele produz resultados muito bons,
podendo inclusive achar o ótimo, como no
exemplo abaixo se iniciarmos em s
s
10
9
7
u
7
5
6
z
10
11
9
v
w
6
Heurísticas para o PCV

Entretanto, em geral, o algoritmo do vizinho
mais próximo pode achar ciclos
hamiltonianos ruins (com custo elevado)
s
1000000
v
2
1
1
2
t
u
1
Heurísticas para o PCV
Aplicações do PVC

Seqüenciamento de tarefas:
Suponha n tarefas que devem ser processadas
numa única máquina
 O tempo necessário para processar a tarefa j
depois da tarefa i é cij
 Como as tarefas devem ser seqüenciadas de
forma a minimizar o tempo de
processamento?
 A solução é um caminho hamiltoniano de
custo mínimo no grafo
