Apresentação do PowerPoint

Teoria das
Estruturas I
Aula 4
Professor Júlio César
INTRODUÇÃO
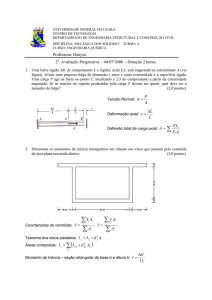
Nesta aula estudaremos como calcular os
valores de momento fletor, a partir das áreas
do diagrama de cortante e calcular uma viga
Gerber.
Fonte: http://banco.agenciaoglobo.com.br/Pa...idimagem=18010
2
Relações matemáticas
dM ( x)
 Q( x)  dM ( x)  Q( x).dx
dx
 dM ( x)   Q( x).dx
M 2 ( x)  M 1 ( x)  Área
dM ( x)
 Q( x)
dx
Quando Q(x) =0,
M(x) é máximo
Área – área sob a curva da função Q(x)
Obs: M(x) grau K+1, Q(x) grau K
3
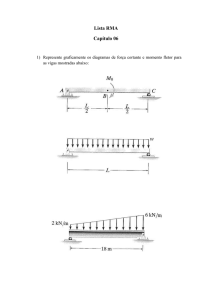
EXEMPLO
Pede-se calcular o momento fletor pela área
do cortante.
4
EXEMPLO - SOLUÇÃO
Determinar as reações VA, VB e HB.
 F x 0
HB  0kN
 F y 0
 M B 0  15x5  4.VA  23x2,5  7 x1  0
VA  VB  15  7  23 x1  0
VA  VB  45kN
 4.VA  75  7  57,5
VA  34,875kN ; VB  10,125kN
5
EXEMPLO – SOLUÇÃO DEC
Segmentos CA, AD, EF, FB - carga concentrada:
DEC formado de retas paralelas à viga. Segmento
DE carga distribuída: DEC é uma função linear.
6
EXEMPLO – SOLUÇÃO DEC
• Cortando-se a viga à direita de C, temos cortante e 15 kN, para baixo. Logo,
- Q - 15 = 0, Q = - 15 kN
• Cortando-se a viga à direita de A, temos para baixo cortante e 15 kN e,
para cima, VA. Logo, VA – 15 – Q’ = 0. Portanto, Q´=19,87kN
• Cortando-se a viga à direita de E, temos para baixo cortante, 15 kN e 23
kN e, para cima, VA. Assim, VA - 23 – 15 – Q” = 0. Logo Q” = -3,13 kN
• Cortando-se a viga à direita de F temos para baixo, cortante, 15 kN, 23kN
e 7kN e, para cima, VA. Assim, VA – 15 – 23 - 7 - Q”’ = 0. Logo, Q´”= 10,13 kN
7
Diagrama do Esforço Cortante - DEC
• O ponto G é a interseção da reta do DEC com a
viga, ou seja, Q(x) é nulo. Portanto, neste ponto, o
momento fletor é máximo.
(semelhança
de triângulos)
19,87
x

 3,13 x  19,87  19,87 x  x  0,864m
3,13 1  x
8
Diagrama do Momento Fletor - DMF
• Áreas dos retângulos de
bases AC e AD: -15 x 1 =
-15 e -19,87 x 1 = -19,87
• Áreas dos triângulos de
bases DG e GE :
0,864x19,87/2 = 8,58 e
0,136x(-3,13)/2 = -0,21
• Áreas dos retângulos de
bases EF e FB: -3,13 x 1
= -3,13 e -10,13x1 = 10,13
9
Vigas Gerber
São vigas decompostas em diversas vigas isostáticas
que as constituem de estabilidade própria e vigas que se
apoiam sobre as demais (sem estabilidade própria).
Fonte : livro Sussekind
10
Vigas Gerber - resolução
As vigas Gerber por serem vigas isostáticas
simples, podem ser calculadas estabelecendo o
equilíbrio
de
cada
uma
delas.
Resolvendo
primeiramente as vigas que não tem equilíbrio próprio
e transmitindo a carga para as vigas com estabilidade
própria. Nas vigas Gerber, as rótulas apresentam
momento nulo.
11
Decomposição das vigas Gerber
• A viga AB – instável
• A viga BC – engastada (estável).
• Primeiramente
determina-se
a
reação em B, a partir da viga
instável AB. Esse valor é transferido
como reação (3a lei de Newton)
para a viga BC.
• A viga AB – instável
• A viga BCD – biapoiada (estável).
• Primeiramente
determina-se
a
reação em B, a partir da viga
instável AB. Esse valor é transferido
como reação (3a lei de Newton)
para a viga BCD.
12
Decomposição das vigas Gerber
13
Determinação das reações
 F y 0
RA  RB  20 X 4  40  0
RA  RB  120kN
 M A 0
 40 X 4  3.RB  80 X 2  0
RB  106,7kN ; RA  13,3kN
 F y 0
RC  40  120  0  RC  160kN
 M C 0
MC 120 x1,5  40 x3  0
MC  300kN .m
14
Diagrama Esforço Cortante - vigas Gerber
Cortando-se a viga à direita de B, temos para baixo
cortante e 60kN, para cima, RA e RB. Logo, 13,3
+106,7 -60 – Q’ = 0. Portanto, Q´=60kN
15
Diagrama Esforço Cortante - vigas Gerber
P
Da semelhança
determinar AP.
entre
triângulos
é
possível
13,3
AP

 AP  0,67 m
46,7 3  AP
16
Diagrama do Momento Fletor - DMF
P
S
• Áreas dos triângulos de
bases AP e PB: (13,3 x
0,67)/2 = 4,4 e (-46,7 x
2,33)/2 = - 54,4
• Área do triângulo de base
SR1: 40x1/2 = 20
• Nas rótulas, momento fletor nulo.
• Lembrando que para cargas distribuídas,
o DMF é uma parábola.
• Área do trapézio:
(- 40 - 160)x3/2 = -300
17
Teoria das
Estruturas I
Atividade
Professor Júlio César
a) Determinação do momento fletor a partir das
áreas do diagrama de cortante;
b) Viga Gerber.
19