GEOMETRIA
CONCEITOS BÁSICOS
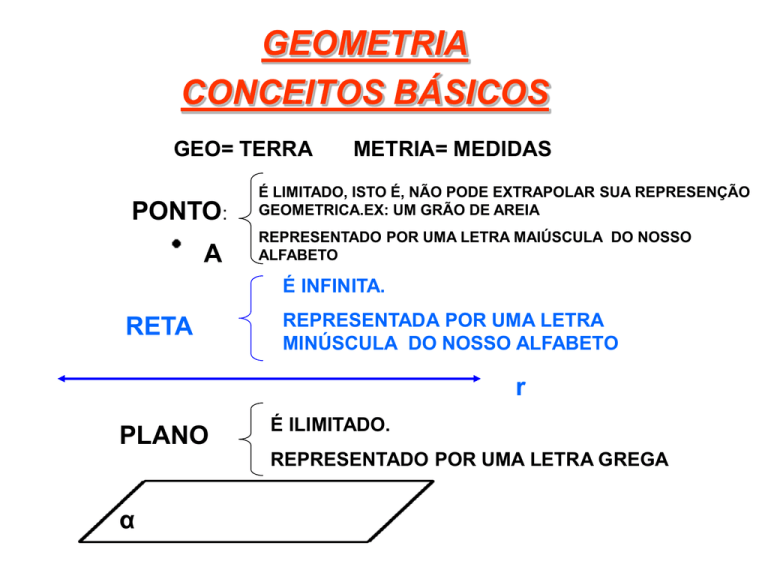
GEO= TERRA
PONTO:
A
METRIA= MEDIDAS
É LIMITADO, ISTO É, NÃO PODE EXTRAPOLAR SUA REPRESENÇÃO
GEOMETRICA.EX: UM GRÃO DE AREIA
REPRESENTADO POR UMA LETRA MAIÚSCULA DO NOSSO
ALFABETO
É INFINITA.
RETA
REPRESENTADA POR UMA LETRA
MINÚSCULA DO NOSSO ALFABETO
r
PLANO
É ILIMITADO.
REPRESENTADO POR UMA LETRA GREGA
α
TUDO QUE EXISTE É FORMADO
POR PONTOS
PODEMOS ENTENDER UMA FIGURA GEOMÉTRICA
(OU OBJETO) COMO A INTERSECÇÃO DE RETAS
CONCORRENTES FORMADAS POR DIVERSOS
PONTOS:
POR UM PONTO PASSAM INFINITAS RETAS.
ALGUMAS FORMAS
GEOMÉTRICAS FECHADAS
AS FORMAS GEOMÉTRICAS FORMADAS POR SEGMENTOS
(PEDAÇOS) DE UMA RETA SÃO CHAMADAS
POLI = MUITOS
GONOS = LADOS
NOMENCLATURA
Nº DE LADOS
•
•
•
•
•
•
•
•
3 LADOS
4 LADOS
5 LADOS
6 LADOS
7 LADOS
8 LADOS
9 LADOS
10 LADOS
NOMES
•
•
•
•
•
•
•
•
TRIÂNGULO
QUADRILÁTERO
PENTÁGONO
HEXÁGONO
HEPTÁGONO
OCTÓGONO
ENEÁGONO
DECÁGONO
•
•
•
•
•
•
•
•
•
•
11 LADOS
12 LADOS
13 LADOS
14 LADOS
15 LADOS
16 LADOS
17 LADOS
18 LADOS
19 LADOS
20 LADOS
•
•
•
•
•
•
•
•
•
•
UNDECÁGONO
DODECÁGONO
TRIDECÁGONO
TETRADECÁGONO
PENTADECÁGONO
HEXADECÁGONO
HEPTADECÁGONO
OCTADECÁGONO
ENEADECÁGONO
ICOSÁGONO
TODO POLÍGONO QUE APRESENTA LADOS E
ÂNGULOS IGUAIS (CONGRUENTES) É CHAMADO
REGULAR
ALGUNS POLÍGONOS
REGULARES
Utilize o programa
cabri II para mais
apresentações
NUM POLÍGONO DESTACAM-SE:
VÉRTICE
LADO
LADO
VÉRTICE
VÉRTICE
LADO
LADO
VÉRTICE
TODA REGIÃO FORMADA DUAS SEMIRRETAS QUE
TÊM A MESMA ORIGEM MAS NÃO ESTÃO CONTIDAS
NA MESMA RETA É CHAMADA ÂNGULO
ÂNGULO
EXTERNO
ÂNGULO
INTERNO
VALE LEMBRAR:
BISSETRIZ DE UM ÂNGULO
BISSETRIZ É UM SEGMENTO COM ORIGEM
NO VÉRTICE DO ÂNGULO QUE O DIVIDE EM
DOIS ÂNGULOS CONGRUENTES, .
Ângulos
complementares
Dois ângulos cuja soma
resulta em 90º são chamados
complementares
Ângulos
suplementares
Dois ângulos cuja soma
resulta em 180º são
chamados suplementares
ângulo
10º
complemento
80º
20º
70º
30º
60º
45º
45º
52º
38º
63,5º
26,5º
70,42º
19,58º
81º
9º
90º
não existe
ângulo
suplemento
10º
170º
30º
150º
45º
135º
63,5º
116,5º
81º
98º
90º
90º
100º
80º
120º
60º
152,5º
27,5º
VOLTANDO AOS POLÍGONOS,
CITAMOS:
• POLÍGONOS CÔNCAVOS
• POLÍGONOS CONVEXOS
NA UNIÃO DE DOIS
PONTOS DESTES
POLÍGONOS POR UM
SEGMENTO DE RETA
ALGUNS PONTOS DO
SEGMENTO FICAM
LOCALIZADOS NA
REGIÃO EXTERNA DO
POLÍGONO
NA UNIÃO DE DOIS
PONTOS DESTES
POLÍGONOS POR UM
SEGMENTO DE RETA,
TODOS PONTOS DESTE
SEGMENTO FICAM
LOCALIZADOS NA
REGIÃO INTERNA DO
POLÍGONO
A SOMA DE UM ÂNGULO INTERNO COM O
EXTERNO EM QUALQUER POLÍGONO
CONVEXO RESULTA EM 180º.
ÂNGULOS OPOSTOS PELO
VÉRTICE
β
α
α=β
SOMA DOS ÂNGULOS
INTERNOS DE UM POLÍGONO
VEJA O QUE ACONTECE EM ALGUNS
POLÍGONOS COM RELAÇÃO AOS
SEUS ÂNGULOS INTERNOS :
180º
360º
360º
+
180º=
540º
Utilize o programa cabri II
para demonstrar a soma
dos ângulos internos
PARTINDO DE UM ÚNICO VÉRTICE, DESCUBRA
QUANTOS TRIÂNGULOS SÃO POSSÍVEIS DE SEREM
FORMADOS EM CADA FIGURA PLANA, UNINDO
VÉRTICES OPOSTOS:
?
1 TRIÂNGULO=
180º
3 TRIÂNGULOS=
COMO EM CADA
540º
TRIÂNGULO A SOMA
DOS ÂNGULOS
INTERNOS É 180º ,
TEMOS:
2 TRIÂNGULOS=
360º
4 TRIÂNGULOS=
720º
6 TRIÂNGULOS=
1080º
PERCEBE-SE:
NOME DA FIGURA
Nº DE LADOS
Nº DE TRIÂNGULOS
SOMA DOS ÂNGULOS
INTERNOS
TRIÂNGULO
3
1
180º
QUADRILÁTERO
4
2
360º
PENTÁGONO
5
3
540º
HEXÁGONO
6
4
720º
HEPTÁGONO
7
5
900º
OCTÓGONO
8
6
1080º
ENEÁGONO
9
7
1260º
DECÁGONO
10
8
1440º
.
.
.
.
.
.
.
.
.
.
.
.
COM n LADOS
n
n-2
(n – 2).180º
EM QUALQUER POLÍGONO CONVEXO A
SOMA DOS ÂNGULOS EXTERNOS É 360º
CHAMAMOS DIAGONAL DE UM
POLÍGONO O SEGMENTO DE RETA QUE
UNE DOIS VÉRTICES OPOSTOS :
2 DIAGONAIS
5 DIAGONAIS
CONTE NESTE...
9 DIAGONAIS
COMO DE CADA VÉRTICE
SEGUEM 5 DIAGONAIS,
PODEMOS ENTENDER COMO 5 x
8 VÉRTICES = 40. COMO CADA
DIAGONAL SERÁ CONTADA
DUAS VEZES, 40 / 2 = 20
PERCEBE-SE:
NOME DA FIGURA
Nº DE LADOS
NÚMERO DE DIAGONAIS
TRIÂNGULO
3
0
QUADRILÁTERO
4
2
PENTÁGONO
5
5
HEXÁGONO
6
9
HEPTÁGONO
7
14
OCTÓGONO
8
20
ENEÁGONO
9
27
DECÁGONO
10
35
.
.
.
.
.
.
.
.
.
n
(n-3).n
2
COM n LADOS
UNIDADE DE MEDIDA
• METRO:
UNIDADE PADRÃO QUE CORRESPONDE
A DÉCIMA MILIONÉSIMA PARTE DE
UM ARCO TERRESTRE QUE LIGA A
CIDADE DE PARIS AO POLO NORTE.
SEUS MÚLTIPLOS E
SUBMÚLTIPLOS
• km (Quilômetro) = 1000 metros
• hm (Hectômetro)= 100 metros
• dam (Decâmetro) = 10 metro
• dm (Decímetro) = 1/10 do metro
• cm (Centímetro)= 1/100 do metro
• mm (Milímetro) = 1/1000 do metro
km
hm dam
m
dm
cm
mm
PARA TRANSFORMAR UNIDADES DE
MEDIDAS USA-SE “MOVER” A VÍRGULA PARA
A DIREITA OU ESQUERDA CONFORME
SOLICITADO:
•
•
•
•
•
TRANSFORME NAS UNIDADES PEDIDAS
2 km = 2000 m
• 2,4 km = 240
2,45 hm = 24500 cm
• 0,08 hm = 80
435 mm = 0,0435 dam
• 43 mm = 0,43
2,35 cm = 0,0235 m
• 235 cm = 2,35
15 m = 0,015 km
• 15 dm = 0,15
km
hm
2
3 unidades
0,0435
dam
m
2,000
dm
4 unidades
cm
dam
dm
dm
m
dam
mm
435
PERÍMETRO
É A SOMA DAS MEDIDAS DOS LADOS DE
UMA FIGURA PLANA
NÃO SE DEVE ADICIONAR UNIDADES DE
MEDIDAS DIFERENTES
FAÇA A
TRANSFORMAÇÃO
QUANDO PRECISO
ÁREA DE UMA FIGURA PLANA
QUANTOS QUADRADOS COMO O
INDICADO NA FIGURA CABEM NO
RETÂNGULO?
1cm
ÁREA DO
QUADRADO=
1cm2
ÁREA É A QUANTIDADE QUE
UMA UNIDADE MENOR
“CABE” EM OUTRA MAIOR
ÁREA DO RETÂNGULO= base x altura = b.h
ÁREA DO
RETÂNGULO
= 18 cm2
ÁREA DO
QUADRADO=
LADO X LADO
NOS TRIÂNGULOS TEMOS:
A=b.h
2
TRIÂNGULO EQUILÁTERO
EM QUALQUER TRIÂNGULO
CONHECENDO SUAS MEDIDAS
A
p( p x).( p y).( p z )
OUTROS POLÍGONOS
• LOSANGO
• TRAPÉZIO
A= b.h.2
+
A = d.D ou
A= (B + b).h
2
ou
B.h + b.h
2
2
HEXÁGONO
OUTROS POLÍGONOS
RECORTE-OS,
ACHANDO A ÁREA
SEPARADAMENTE E
SOME OS
RESULTADOS
OBTIDOS
A= 6 TRIÂNGULOS
EQUILÁTEROS
A= ÁREA DO TRIÂNGULO +
+ ÁREA DO TRAPÉZIO
NO CÍRCULO
COMPRIMENTO DA
CIRCUNFERÊNCIA = 2. r.
ÁREA DO CÍRCULO = r2.
CORDA
RAIO
DIÂMETRO
Comprimento x raio
2
=
=r².
=3,1416...
Veja porquê:
EM QUALQUER
CÍRCULO A
DIVISÃO ENTRE
O SEU
COMPRIMENTO
E SEU
DIÂMETRO
RESULTA EM
3,1416...
PERCEBE-SE:
=
Como d = 2r
POSIÇÕES DE UM PONTO P
E UMA CIRCUNFERÊNCIA
P é externo
P é interno
x
x
w
y
w
y
z
z
Teorema
de Thales
TRIÂNGULOS
CONDIÇÃO DE EXISTÊNCIA:
UM TRIÂNGULO SÓ EXISTE SE A SOMA DAS
MEDIDAS DE DOIS LADOS QUAISQUER FOR
MAIOR QUE A MEDIDA DO TERCEIRO LADO
3 cm
6 cm
3 cm
2 cm
6 cm
7 cm
3+6>7
2+3<6
SÃO CLASSIFICADOS ...
QUANTO AOS LADOS:
ESCALENO = TODOS OS LADOS TÊM MEDIDAS
DIFERENTES
ISÓSCELES = DOIS DE SEUS LADOS SÃO
CONGRUENTES, OU SEJA, TÊM
MEDIDAS IGUAIS
EQUILÁTERO = PREFIXO EQUI QUER DIZER IGUAL E
LÁTERO É LADO, LOGO, OS 3 LADOS
SÃO IGUAIS
SÃO CLASSIFICADOS ...
QUANTO AOS ÂNGULOS:
ACUTÂNGULO =TODOS OS ÂNGULOS SÃO AGUDOS,
OU SEJA, MENORES QUE 90º
OBTUSÂNGULO = APRESENTA UM ÂNGULO OBTUSO,
OU SEJA, MAIOR QUE 90º
RETÂNGULO=
É AQUELE QUE TEM UM ÂNGULO
RETO, OU SEJA, IGUAL A 90º
ÂNGULO RETO
ALTURA
MEDIANA
MEDIATRIZ
M
h
M
h
M
M
h
M
segmento de reta
perpendicular
M
Segmento de reta
Divide o lado oposto em 2 perpendicular aos lados
segmentos congruentes traçada pelos pontos médios
É BOM SABER:
O ponto de
interseção das
alturas é o
ortocentro
O circuncentro é o
centro da
circunferência
circunscrita ao
triângulo.
O ponto de interseção
das três medianas é o
baricentro ou centro de
gravidade.
COMO THALLES MEDIU A
ALTURA DA GRANDE
PIRÂMIDE:
Raios
solares
Altura da
pirâmide(H)
Estaca (h)
Sombra da
estaca (s)
Base/2
Sombra da pirâmide (S)
Este é um caso de semelhança de
triângulos
• Triângulos são considerados semelhantes
quando se igualam na forma nas medidas
de seus ângulos, porém, diferem quanto a
medidas de seus lados.
Quanto a sua praticidade podemos
A sombra de uma
citar:
pessoa que tem
1,80m de altura
mede 60cm. No
mesmo momento,
a seu lado, a
sombra projetada
de um poste mede
2,00m. Se, mais
tarde, a sombra do
poste diminuiu
50cm, a sombra da
pessoa passou a
medir:
• a) 30 cm
• b) 45 cm
• c) 50 cm
• d) 80 cm
• e) 90 cm
x
1,80
60 cm = 0,6 m
6m
1,80
2m
Com a sombra do poste
diminuindo em 50 cm, temse:
y
TRIÂNGULO RETÂNGULO
É AQUELE QUE APRESENTA UM ÂNGULO
RETO (90º)
NELE DESTACAM-SE:
O LADO MAIOR É A
HIPOTENUSA (À FRENTE DO
ÂNGULO RETO
(a)
(b)
(c)
OS OUTROS LADOS SÃO
OS CATETOS
TEOREMA DE PITÁGORAS
OS QUADRADOS
A POSSUEM
HIPOTENUSA
ÁREAS
A 9 E 16
AOIGUAIS
QUADRADO
É IGUAL
A SOMA
O QUADRADO
MAIOR TEM ÁREA
DOS
IGUAL A 25
QUADRADOS
LOGO, SEU
DOSLADO
CATETOS
MEDE 5,
POIS 5²= 25
OU
a²DEFINI-SE,
= b² + ENTÃO:
c²
RELAÇÕES MÉTRICAS EXISTENTES NO
TRIÂNGULO RETÂNGULO:
CONHEÇA MAIS ALGUNS ELEMENTOS NESTE
TRIÂNGULO
b
m
PROJEÇÃO DO CATETO
(b) SOBRE A
HIPOTENUSA
ALTURA RELATIVA
À HIPOTENUSA
h
c
n
PROJEÇÃO DO CATETO
(c) SOBRE A
HIPOTENUSA
Considere o quadrado de lado a e área a²
b
a
a
h
c
Dividindo
Perceba os
o triângulo
triângulos
abc,
A área do triangulo de
retângulos de
temos:
catetos b e c
lados abc é dada por
a² = b² + c²
c.b ...
2
a=m+n
aou...
.h = b.c
Teorema de
Pitágoras
h
a² = b² + c²
a
a.h
2
Logo, c.b =a.h, daí:
2
2
a.h = b.c
Para melhor entendimento mostra-se a medida dos lados do triângulo
B
h² = (10 - n)² - 64 ( I )
e
8 cm
6 cm
h
m
A
n
10 cm
D
m + n = 10, logo, m = 10 – n.
Igualando (I) e (II) tem-se:
C
Por Pitágoras, no triângulo ADB temos:
8² = h² + m²
h² = n² - 36 ( II )
(10 - n)² - 64 = n² - 36
n = 3,6
e no triângulo CDB temos:
6² = h² + n²
Trocando m por 10 – n e
isolando no 1º termo h²
tem-se:
Se n= 3,6, então, m= 6,4
e h = 4,8
Como
• 8² = 10 x 6,4
b² = a . m
B
c = 6 cm
b=8
h = 4,8
m = 6,4
A
a = 10
• 6² = 10 x 3,6
c² = a . n
n =3,6
C
• 10 x 4,8 = 6 x 8
a . h = b .c
• 10 = 6,4 + 3,6
a=m+n
• 4,8² = 6,4 x 3,6
h² = m . n
TRIGONOMETRIA
• TRIGONO = TRIÂNGULOS
• METRIA = MEDIDAS
É A PARTE DA MATEMÁTICA QUE
ESTUDA AS RELAÇÕES E RAZÕES
EXISTENTES ENTRE OS LADOS DO
TRIÂNGULO E SEUS ÂNGULOS.
Cateto
oposto à αà β
Catetoadjacente
CONSIDERE O TRIÂNGULO
RETÂNGULO ABAIXO:
O lado do triângulo
que “forma” o
ângulo
com a
O lado junto
do triângulo
hipotenusa
é do
situado
à frente
chamado
cateto
ângulo
é chamado
adjacente
cateto
oposto
β
α
Cateto
Catetoadjacente
oposto à àβ α
α é um ângulo
agudo
Observe a seqüência de triângulos semelhantes
Essa razão é chamada seno
de um ângulo
Essa razão é chamada coseno
de um ângulo
Essa razão é chamada
tangente de um ângulo
20
15
12
9
10
5
6
3
16
12
8
4
RELAÇÕES MÉTRICAS NUM TRIÂNGULO QUALQUER
• LEI DOS SENOS
DO
DO VÉRTICE
VÉRTICE C
A
B
OBSERVE
O
TRIÂNGULO
ESCALENO
TRAÇAMOS
UM
TRAÇAMOS UM
INSCRITO
NUMA
CIRCUNFERÊNCIA DE
SEGMENTO
PASSANDO
SEGMENTO PASSANDO
RAIO R
PELO
CENTRO
PELO CENTRO
C
2R
β
A
Cateto oposto a α
γa
a
= b
=
c
Senα
Sen β
Senγ
Senα=
Senγ
Sen β=__c__
=_b_
_a_ 2R
2R
2R===_b_
_c_
a__
2R
2R
2R
Sen
Senα
Senγ
β
bα
c
=
B
EM QUALQUER TRIÂNGULO
ABC, AS MEDIDAS DOS LADOS
SÃO PROPORCIONAIS AOS
SENOS DOS ÂNGULOS
OPOSTOS
• LEI DOS COSSENOS
CONSIDERE O ÂNGULO A DO TRIÂNGULO
No triângulo ABH temos:
No triângulo CBH temos:
a2 = (b –m)2 + h2
c2 = m2 + h2
h2 = a2 – (b – m)2
Daí:
c 2 = (cosA.c)2 + h2
De (I) = (II) temos
a2 = b2 + c2 – 2.b.c.cosA
h2 = (cosA.c)2 - c 2
h2 = cos2 A.c2 - c 2
(II)
(I)
h
b-m
m
H
O quadrado da medida
de um lado é igual a
soma dos quadrados
das medidas dos outros
dois lados menos duas
vezes o produto desses
lados pelo cosseno do
ângulo que eles formam
ESTUDA OS SÓLIDOS GEOMETRICOS, SUAS RELAÇÕES,
CARACTERÍSTICAS E PARTICULARIDADES
CORPOS REDONDOS
DIVIDIMOS
EM DOIS
GRANDES
GRUPOS
POLIEDROS
É
IMPORTANTE
SABER:
DUASRETAS
OU
MAIS
COPLANARES
RETAS
SÃOQUE
COPLANARES
TEMNÃO
TODOS
QUANDO
OS
EXISTE
•RETAS
COPLANARES
QUE
TEM
UMPONTOS
PONTO
EM CADA PLANO, HÁ INFINITAS RETAS
RETASEM
COPLANARES
NO
ESPAÇO
HÁ
QUE
INFINITOS
TEM
ÚNICO
PLANOS
PONTO EM
COMUM
UM PLANO
SÃO
CHAMADAS
QUE
ASUM
CONTÉM
COINCIDENTES
EM
COMUM
SÃO
CHAMADAS
PARALELAS
COMUM SÃO CHAMADAS CONCORRENTES
t
α
r
s
r
r
r
s
s
Retas
reversas ou
nãocoplanares
são retas
que estão
em plano
distintos
r xr s//s//t
xt
s
t
r é reversa à s
POLIEDROS
• SÓLIDOS GEOMÉTRICOS CUJAS
FACES SÃO POLÍGONOS.
vértices
faces
arestas
NOMENCLATURA
Nº DE FACES
•
•
•
•
•
•
•
4 FACES
5 FACES
6 FACES
7 FACES
8 FACES
9 FACES
10 FACES
NOMES
•
•
•
•
•
•
•
TETRAEDRO
PENTAEDRO
HEXAEDRO
HEPTAEDRO
OCTAEDRO
ENEAEDRO
DECAEDRO
Nº DE FACES
•
•
•
•
•
•
•
•
•
•
11 FACES
12 FACES
13 FACES
14 FACES
15 FACES
16 FACES
17 FACES
18 FACES
19 FACES
20 FACES
NOMES
•
•
•
•
•
•
•
•
•
•
UNDECAEDRO
DODECAEDRO
TRIDECAEDRO
TETRADECAEDRO
PENTADECAEDRO
HEXADECAEDRO
HEPTADECAEDRO
OCTADECAEDRO
ENEADECAEDRO
ICOSAEDRO
Para facilitar a construção...
Número de vértices, arestas e
faces num poliedro
1
1
6
3
4
1
3
5
4
5
Vértices= 84
Faces= 46
6
7
3
2
4
4
2
2
8
arestas=
612
1
3
2
VERIFIQUE NESTES POLIEDROS
NOME
FACES
VÉRTICES
ARESTAS
OCTAEDRO
8
6
12
TRONCO DA PIRÂMIDE
6
8
12
PIRÂMIDE
7
7
12
PRISMA
5
6
9
NOTE QUE A QUANTIDADE DE ARESTAS,
É DUAS UNIDADES MENOR QUE A SOMA
DAS FACES E VÉRTICES:
NOME
FACES
VÉRTICES
ARESTAS
OCTAEDRO
8
6
12
TRONCO DA PIRÂMIDE
6
8
12
PIRÂMIDE
7
7
12
PRISMA
5
6
9
FACES + VÉRTICES = ARESTAS + 2
RELAÇÃO DE EULLER
POLIEDROS DE PLATÃO
• PORQUE TEM
POLÍGONOS
REGULARES
IGUAIS COMO
FACES E
QUALQUER FACE
QUE ESTIVER NA
POSIÇÃO
INFERIOR NÃO
ALTERA A
APRESENTAÇÃO
EXISTEM
SOMENTE
CINCO
POLÍGONOS
REGULARES
CONVEXOS
PLANIFICAÇÃO DE
POLIEDROS
• CUBO
• PARALELEPÍPEDO • TETRAEDRO
RETO RETÂNGULO
UTILIZE O PROGRAMA POLY
E VEJA MAIS
PLANIFICAÇÕES
• PRISMA DE BASE
HEXAGONAL
• CILINDRO
• PIRÂMIDE DE
• ICOSÁEDRO
BASE HEXAGONAL
• PIRÂMIDE DE
BASE QUADRADA
• PENTAEDROS
• OCTAEDRO
• HEPTAEDRO
OU PRISMA DE
BASE
PENTAGONAL
DODECAEDRO
PRISMAS
Tal como nos polígonos, os
poliedros também podem ser
convexos e não-convexos.
POLIEDROS CONVEXOS
POLIEDROS NÃO-CONVEXOS
Obs. O estudo a partir daqui vai considerar
apenas os polígonos convexos. Por isso, quando
aparecer a palavra polígono considere-o convexo
CUBO
•ÁREA DA BASE = l2
•ÁREA TOTAL = 6 l2
•ÁREA LATERAL = 4l2
•VOLUME = l3
ou ÁREA DA BASE x ALTURA
DIAGONAL DA BASE E DO CUBO
POR PITÁGORAS...
DIAGONAL
DO CUBO
l
3
l
DIAGONAL
DA BASE
2
PARALELEPÍPEDO RETO RETÂNGULO
ÁREA DA BASE = a.b
ÁREA LATERAL = 2.(a.c + b.c)
ÁREA TOTAL = 2.ÁREA DA BASE + ÁREA LATERAL
ou 2.Ab + Al
VOLUME = ÁREA DA BASE x ALTURA (c)
a
ou a.b.c
DIAGONAL...
b
b
a
c
a
c
b
b
c
c
d
x
a POR PITÁGORAS...
x2 = a2 + b2, logo
d2 = c2 + x2
OUTROS PRISMAS DE BASES POLIGONAIS:
• BASE TRIANGULAR
• BASE HEXAGONAL
ÁREA DA BASE = (ÁREA DO
POLIGONO QUE A FORMA)
ÁREA TOTAL = 2.AB + AL
VOLUME= AB.h
= ÁREA LATERAL =
PIRÂMIDES
•
PIRÂMIDE DE
BASE QUADRADA
•
PIRÂMIDE DE BASE
TRIÂNGULAR
•
PIRÂMIDE DE BASE
HEXAGONAL
ELEMENTOS
ALTURA
APÓTEMA DA
PIRÂMIDE
ALTURA DE CADA FACE
APÓTEMA DA
BASE
BASE
TODAS AS FACES
LATERAIS SÃO
TRIANGULARES
CÁLCULO DO APÓTEMA DA BASE (m)
BASE QUADRADA
BASE TRIANGULAR
BASE HEXAGONAL
a
m
METADE DO LADO
DA BASE
a
m=
2
h
m
UM TERÇO DA
ALTURA DO
TRIÂNGULO
m=
h
3
a h=m
ALTURA DE UM
DOS TRIÂNGULOS
QUE FORMAM O
HEXÁGONO
CÁLCULO DO APÓTEMA DA PIRÂMIDE (g)
g
g
h
g
m
h
h
m
g2 = m2 + h2
m
ÁREAS
ÁREA DA BASE = (ÁREA DO POLIGONO QUE A FORMA)
ÁREA LATERAL = a.g.n , sendo n a quantidade de faces
2
laterais
ÁREA TOTAL = AB + AL
Volume do cubo =
l³= 6³ = 216
VOLUME
VEJA O CUBO DE LADO 6
Traçam-se as 4
diagonais.(lembre-se
a diagonal do cubo é
6 3
Destaca-se uma
pírâmide de altura
6/2 = 3
Note que há 6
pirâmides iguais a
essa
Logo, o volume de cada
pirâmide é 216/6 = 36
Se a base da
pirâmide é 6, e
sua altura é 3,
definimos:
V= AB.h
3
TRONCO DE PIRÂMIDES DE BASES
PARALELAS
CONSIDERE UM PLANO α PARALELO À BASE DE
UMA PIRÂMIDE, SEPARANDO-A EM 2 POLIEDROS:
TRONCO DA
PIRÂMIDE É A
DISTÂNCIA
ESTABELECIDA
ENTRE AS DUAS
BASES
PARALELAS E A
ALTURA DO
TRONCO
VOLUME DO TRONCO:
V= VOLUME DA PIRÂMIDE MAIOR – VOLUME DA PIRÂMIDE MENOR
AB.(k + h) – Ab.h
3
h
K
ou
K
V
B Bb B
3
A ÁREA TOTAL É OBTIDA PELA
ÁREA DOS TRAPÉZIOS QUE
FORMAM A LATERAL DO
TRONCO E DE SUAS BASES
Na prática é mais adequado utilizar a subtração entre os volumes
das pirâmides para obter o volume do tronco, porém, fica a
critério de cada um decidir qual processo será utilizado.
CILINDRO
PLANIFICAÇÃO
• ELEMENTOS
ÁREA LATERAL= (Comprimento).(altura)
ÁREA DA BASE = r2
ÁREA TOTAL = 2 Ab + Al
VOLUME = Ab.h
BASES
COMPRIMENTO DA
CIRCUNFERÊNCIA
(BASE)
2 r
Sólido limitado
pela superfície
gerada por uma
reta que desliza
sobre um ponto
fixo no espaço
(vértice) e pelo
plano da curva
diretriz
CONE
PLANIFICAÇÃO
ALTURA
GERATRIZ
CÍRCULO
SETOR
CIRCULAR
RAIO
ELEMENTOS
ÁREAS E VOLUMES
ÁREA DA BASE=
(ÁREA DO CÍRCULO)
R
ÁREA LATERAL
(ÁREA DO SETOR
CIRCULAR)
g
ÁREA TOTAL = AB + AL
VOLUME
V= AB.h
3
ou
TRONCO DO CONE
P
L
B
A
R
N
I
h
g
F
Área da base menor:
b
r
I
C
Área da Base maior:
A
Área Lateral:
Ç
Área Total:
Volume:
AB + Ab + AL
Ã
O
ESFERAS
ELEMENTOS
RAIO
CÍRCULO MÁXIMO
VOLUME
PRINCÍPIO DE CAVALIERI
DAÍ, ESTABELECE-SE:
4
• VOLUME =
3
• ÁREA = 4 R2
R3
ALGUMAS FIGURAS QUE PODEM SER COPIADAS PARA
ELABORAÇÃO DE ATIVIDADES
PARA TANTO BASTA CLICAR SOBRE ELAS...
(NÃO NO MODO DE EXIBIÇÃO)
AS FIGURAS
ESTÃO
REMONTADAS.
ARRASTE-AS
towerofhanoi.exe
Ficha técnica:
CONTEÚDO : GEOMETRIA
EIXO: NÚMEROS, OPERAÇÕES E FUNÇÕES
HABILIDADES E COMPETÊNCIAS:
ENTENDER O SIGNIFICADO DA GEOMETRIA, SEUS PRINCíPIOS E
SUAS RELAÇÕES .
RECONHECER AS FORMAS GEOMETRICAS E SEUS ELEMENTOS.
SABER RESOLVER CORRETAMENTE ATIVIDADES DO COTIDIANO
QUE ENVOLVE ESSES ELEMENTOS E RELAÇÕES.
ELABORADO POR CLECIO GERALDO ZANETTI
[email protected]












