Efeito Magnus

TC de MHS
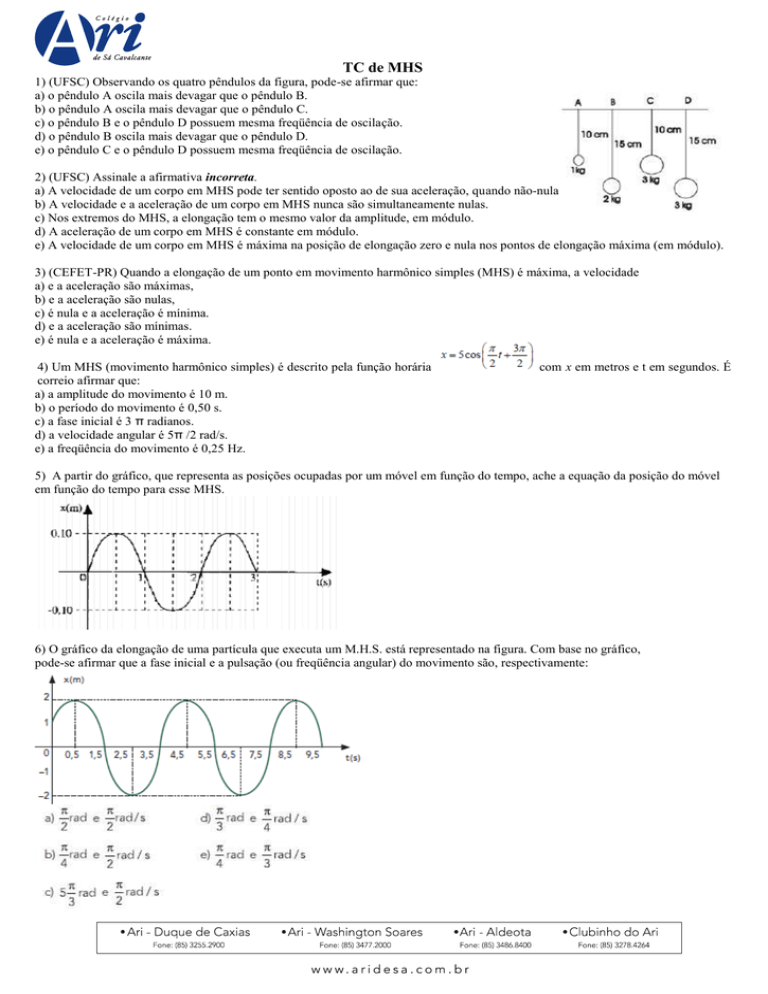
1) (UFSC) Observando os quatro pêndulos da figura, pode-se afirmar que:
a) o pêndulo A oscila mais devagar que o pêndulo B.
b) o pêndulo A oscila mais devagar que o pêndulo C.
c) o pêndulo B e o pêndulo D possuem mesma freqüência de oscilação.
d) o pêndulo B oscila mais devagar que o pêndulo D.
e) o pêndulo C e o pêndulo D possuem mesma freqüência de oscilação.
2) (UFSC) Assinale a afirmativa incorreta.
a) A velocidade de um corpo em MHS pode ter sentido oposto ao de sua aceleração, quando não-nula.
b) A velocidade e a aceleração de um corpo em MHS nunca são simultaneamente nulas.
c) Nos extremos do MHS, a elongação tem o mesmo valor da amplitude, em módulo.
d) A aceleração de um corpo em MHS é constante em módulo.
e) A velocidade de um corpo em MHS é máxima na posição de elongação zero e nula nos pontos de elongação máxima (em módulo).
3) (CEFET-PR) Quando a elongação de um ponto em movimento harmônico simples (MHS) é máxima, a velocidade
a) e a aceleração são máximas,
b) e a aceleração são nulas,
c) é nula e a aceleração é mínima.
d) e a aceleração são mínimas.
e) é nula e a aceleração é máxima.
4) Um MHS (movimento harmônico simples) é descrito pela função horária
correio afirmar que:
a) a amplitude do movimento é 10 m.
b) o período do movimento é 0,50 s.
c) a fase inicial é 3 π radianos.
d) a velocidade angular é 5π /2 rad/s.
e) a freqüência do movimento é 0,25 Hz.
com x em metros e t em segundos. É
5) A partir do gráfico, que representa as posições ocupadas por um móvel em função do tempo, ache a equação da posição do móvel
em função do tempo para esse MHS.
6) O gráfico da elongação de uma partícula que executa um M.H.S. está representado na figura. Com base no gráfico,
pode-se afirmar que a fase inicial e a pulsação (ou freqüência angular) do movimento são, respectivamente:
7) Um corpo apresenta MHS tal que sua velocidade máxima é 6 m/s, e sua aceleração máxima é 36 m/s2. Esse
movimento apresenta, respectivamente, amplitude e período de: (considere  = 3)
a) 1 m e 1 s
b) 1 m e 6 s
c) 36 m e 6 s
d) 4 m e 1 s
8) Um corpo de 100 g, preso a uma mola ideal de constante elástica 2.10 3 N/m, descreve um MHS de amplitude
20 cm, como mostra a figura. A velocidade do corpo quando sua energia cinética é igual à potencial, é:
a) 20 m/s
b) 16 m/s
c) 14 m/s
d) 10 m/s
e) 5 m/s
9) Uma partícula oscila ligada a uma mola leve, executando movimento harmônico simples de amplitude 2,0 m. O
diagrama representa a variação de energia potencial elástica Ep, acumulada na mola, em função da elongação da partícula (x). Podese afirmar que a energia cinética da partícula, no ponto de elongação x = 1,0 m, vale:
a) 3,0 . 103 J
b) 2,0 . 103 J
c) 1,5 . 103 J
d) 1,0 . 103 J
e) 5,0 . 103 J
10) Um sistema oscilante massa-mola possui uma energia mecânica igual a 1,0 J, uma amplitude de oscilação 0,5 m e uma velocidade
máxima igual a 2m/s. Portanto, a constante da mola, a massa e a freqüência são, respectivamente, iguais a:
a) 8,0 N/m, 1,0 kg e 4/  Hz
b) 4,0 N/m, 0,5 kg e 4/  Hz
c) 8,0 N/m, 0,5 kg e 2/  Hz
d) 4,0 N/m, 1,0 kg e 2/  Hz
11) Suponha que um pequeno corpo, de massa m, esteja preso na extremidade de um fio de peso desprezível,
cujo comprimento é L, oscilando com pequena amplitude, em um plano vertical, como mostra a figura a seguir. Esse
dispositivo constitui um pêndulo simples que executa um movimento harmônico simples. Verifica-se que o corpo, saindo de B,
desloca-se até B' e retorna a B, 20 vezes em 10 s. Assinale V para o que for verdadeiro e F para o que for falso.
(
(
(
) O período deste pêndulo é 2,0 s.
) A freqüência de oscilação do pêndulo é 0,5 Hz.
) Se o comprimento do fio L for 4 vezes maior, o período do pêndulo será dobrado.
(
(
(
) Se a massa do corpo suspenso for triplicada, sua freqüência ficará multiplicada por 3 .
) Se o valor local de g for 4 vezes maior, a freqüência do pêndulo será duas vezes menor.
) Se a amplitude do pêndulo for reduzida à metade, seu período não modificará.
12) Um movimento harmônico simples é descrito pela função x=0,050 cos(2™t+™), em unidades do Sistema Internacional. Nesse
movimento, a amplitude e o período, em unidades do Sistema Internacional, valem, respectivamente,
a) 0,050 e 1,0
b) 0,050 e 0,50
c) ™ e 2™
d) 2™ e ™
e) 2,0 e 1,0
13) Uma partícula é suspensa por um fio, de massa desprezível, de 1,6m de comprimento, formando um pêndulo, como mostra a
figura. No ponto P, situado 1,2m, verticalmente, abaixo do ponto O, há um prego que impede a passagem do fio. A partícula é liberada
quando o fio forma um ângulo š, muito pequeno, com a vertical. Quando o fio encontra o prego, a partícula continua seu movimento
até atingir o ponto mais alto de seu percurso. Calcule o tempo que ela leva desde o ponto inicial até esse ponto final. Considere
g=10m/s£, a aceleração da gravidade no local.
14) (Mackenzie)
Um corpo C, de massa 1,00.10-¢ kg, está preso a uma mola helicoidal de massa desprezível e que obedece à Lei de Hooke. Num
determinado instante, o conjunto se encontra em repouso, conforme ilustra a figura 1, quando então é abandonado e, sem atrito, o
corpo passa a oscilar periodicamente em torno do ponto O. No mesmo intervalo de tempo em que esse corpo vai de A até B, o pêndulo
simples ilustrado na figura 2 realiza uma oscilação completa. Sendo g = 10 m/s£, a constante elástica da mola é:
a) 0,25 N/m
b) 0,50 N/m
c) 1,0 N/m
d) 2,0 N/m
e) 4,0 N/m
15) Uma partícula realiza um MHS em torno do ponto O com período de 2s (figura).
Os pontos M e N são os extremos da oscilação e no instante t=0 a partícula está passando sobre o ponto 0, deslocando-se para a
esquerda.
Pede-se para esse MHS:
a) a freqüência f
b) a pulsação w (velocidade angular)
c) a amplitude
d) a fase inicial
e) a função horária da elongação
16) O gráfico mostra a posição em função do tempo de uma partícula em movimento harmônico simples (MHS) no
intervalo de tempo entre 0 e 4 s. A equação da posição em função do tempo para este movimento é dada por
x=A. cos(  0 +
 .t). A partir do gráfico, encontre os valores das constantes A,  e  0 .
17) O gráfico da elongação x=A cos(  0 +
 .t). de uma partícula que executa um movimento harmônico simples está
representado na figura. Determine a fase inicial, a pulsação ou freqüência angular e a função horária da elongação desse movimento.
18) Um M.H.S. (movimento harmônico simples) é descrito pela função horária x = 5 cos (π t/2 + 3 π /2), com x em metros e t em
segundos. É correto afirmar que:
a) a amplitude do movimento é 10m;
b) a velocidade angular é 5π/2 rad/s;
c) a freqüência do movimento é 0,25Hz;
d) o período do movimento é 0,50s;
e) a fase inicial é 3 π radianos.
19) Um bloco é preso a uma mola de massa desprezível e executa movimento harmônico
simples, sem atrito com o solo horizontal. A energia potencial do sistema é zero na posição de
elongação nula e pode assumir valor máximo de 60 joules durante o movimento.
Quando a elongação é metade do valor da amplitude, a energia cinética do bloco, em joules, é:
a)15 b)20
c)30
d)40
e)45
20) Um corpo de 2Kg, preso a uma mola ideal de constante elástica 2 .103 N/m, descreve um MHS de amplitude 20 cm,
como mostra a figura. Calcule a velocidade do corpo quando esse corpo passa pela posição 10 cm.