Probabilidade - UFMT

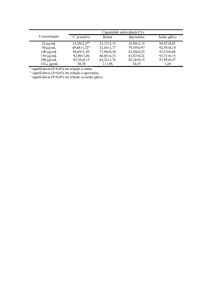
Probabilidade
(Biometria)
Teste do Quiquadrado
Livro texto:
Genética na Agropecuária (Biometria)
RAMALHO, M.A.P., SANTOS, J.B., PINTO, C.A.B.P. 2ª ed. Lavras UFLA,
2000
Genética Básica On-Line
(Probabilidade)
Profº: Glauco Vieira de Oliveira
INTRODUÇÃO
Entre os testes de avaliação de hipóteses genéticas, o teste de x² tem
se mostrado bastante útil e eficiente, pois leva em consideração
os desvios ocorridos entre valores previstos e observados e é
sensível ao tamanho da amostra.
•
NÍVEL DE SIGNIFICÂNCIA PRÉ-ESTABELECIDO
para se testar uma hipótese genética, é necessário obter duas
estatísticas denominadas x² calculado e x² tabelado.
– O x² calculado é obtido a partir dos dados experimentais, levando-se em
conta os valores observados e aqueles que seriam esperados dentro da
hipótese genética formulada.
– O x² tabelado depende dos graus de liberdade e do nível de significância
adotado. A tomada de decisão é feita comparando-se o valor do x² obtido
com base nos resultados observados com o valor do x² apresentado nas
tabelas.
NÍVEL DE SIGNIFICÂNCIA PRÉ-ESTABELECIDO
•
•
As seguintes decisões devem ser tomadas:
• Se x² calc  x² tab => Rejeita-se Ho
• Se x² calc < x² tab => Não se rejeita Ho
Ho refere-se à hipótese formulada a respeito do caráter que se
está estudando.
O valor do x² tabelado é encontrado em vários livros de
estatística, sendo obtido para um determinado nível de
significância (alfa) e certos graus de liberdade.
O grau de liberdade, na maioria das vezes, é igual ao número de
classes fenotípicas menos 1.
O nível de significância (alfa) representa a máxima
probabilidade de erro que se tem ao rejeitar uma hipótese.
Exemplo 1) Aplicação do 2 a uma Distribuição
Binomial
Exemplo slide anterior
Distribuição de dois descendentes de cada uma das 100 vacas de
acordo com o sexo
Nº de vacas
Observadas
Sexo dos
descendentes
Probabilidade
Nº de vacas
Esperado
24
2 fêmeas
¼
25
54
1 macho e 1 fêmea
½
50
22
2 machos
¼
25
Estes desvios ocorrem ao acaso ou não?
Estes desvios são pequenos o suficiente para não rejeitar a hipótese de que a
distribuição desta caráter (sexo) é binomial?
O
E
24
25
54
50
22
25
= (soma)
d=(O-E)
d2/E
Os graus de liberdade são:
GL = n-1 = 3-1 = 2.
0
Valor de quiquadrado (2)
Exemplo 2) Aplicação do teste 2 aos dados da geração F2,relativo
ao estudo da herança da cor e textura da semente de milho
Fenótipo
O
E
Desvio
(O – E)
Amarela lisa
268 270
Amarela enrugada 86 90
Branca lisa
97 90
-2
-4
+7
Branca enrugada
-1
29
30
d2
d2/E
Somatório ()
 2  [(O  E)2 / E]
x² calculado = [(268-270)²/270] + [(86-90)²/90] + [(97-90)²/90] + [(29-30)²/30] = 0,77
Os graus de liberdade são: GL = n-1 = 4-1 = 3.
Exemplo3) Aplicação do teste 2
cruzamento entre plantas de frutos alongados
Testando a hipótese de que o caráter é regulado por 2 genes com
interação não-epistática, segregando na proporção 9:3:3:1.
2
2


[(
O

E
)
/ E]
Fórmula:

x²calc = [(860-900)²/900] + [(280-300)²/300] + [(350-300)²/300] + [(110-100)²/100] =
12,44
Os graus de liberdade são: GL = n-1 = 4-1 = 3.
Conclusão sobre exercício 1, 2 e 3
Valores de 2 para diferentes níveis de
probabilidade (alfa)
2º exercício
2calc=0,77
Tabelado: 2(5%, gl=3)=7,81
x² calc < x² tab => Não se rejeita Ho
Ou seja não se rejeita a hipótese de que o
caráter segue distribuição fenotípica de
9:3:3:1
Adotando um alfa = 5% para todos os três exercícios
1º exercício
3º exercício
2calc=0,72
2calc=12,44
Tabelado: 2(5%, gl=2)=6
Tabelado: 2(5%, gl=3)=7,81
x² calc < x² tab => Não se rejeita Ho
x² calc > x² tab => Rejeita-se Ho
Ou seja não se rejeita a hipótese de que a
distribuição fenotípica do caráter é de
natureza binomial
Rejeito a hipótese de que o caráter é
regulado por 2 genes com interação nãoepistática, segregando na proporção
9:3:3:1
QUI-QUADRADO - UTILIZAÇÃO E
LIMITAÇÕES
O teste de qui-quadrado, aplicável às análises de
resultados genéticos, tem as seguintes vantagens e
limitações:
•
Vantagens
•
É sensível aos desvios definidos entre valores previstos
e observados e ao tamanho da amostra. O teste exige
que, quanto maior for o tamanho da amostra, menor
sejam os desvios, para que não aconteça a rejeição da
hipótese.
Limitações
QUI-QUADRADO - UTILIZAÇÃO E
LIMITAÇÕES
Limitações
• O teste 2 nunca deve ser utilizado em proporções ou
em porcentagens.
• O teste 2 não é adequado para experimentos em que a
frequencia esperada de qualquer classe fenotípica seja
menor que cinco.
–
Neste caso faz-se necessário uma correção da fórmula, dada por:
  {[( O  E )  0,5] / E ]} 
 correção de Yates
2
2