estat basica aula 5 - Rede Linux IME-USP

Aula 5
ENGENHARIA DA QUALIDADE INTEGRADA
ESTATÍSTICA EM GESTÃO
Probabilidade
Histogramas
Conceito
Como construir e Interpretar Histogramas
Medidas para representar as características de
distribuição
Distribuição Normal e Suas Características
Aplicação – Exemplos práticos
Exercícios de fixação.
Seção 3.1
Conceitos básicos de probabilidade
slide 2
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Objetivos da Seção 3.1
• Identificar o espaço amostral de um experimento de
probabilidade
• Identificar eventos simples
• Usar o princípio fundamental da contagem
• Distinguir probabilidade clássica, empírica e subjetiva
• Determinar a probabilidade dos complementos de um
evento
• Usar um diagrama de árvore e o princípio fundamental
da contagem para encontrar probabilidades
slide 3
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Experimentos de
probabilidade
Experimento de probabilidade
Uma ação, ou tentativa, através da qual resultados específicos
(contagens, medidas ou respostas) são obtidos.
Resultado
O resultado de um único teste em um experimento de probabilidade.
Espaço de amostra
O conjunto de todos os possíveis resultados de um experimento de
probabilidade.
Evento
Consiste de um ou mais resultados e é uma divisão do espaço de
amostra.
slide 4
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
• Experimento de probabilidade: Jogar um dado
• Resultado: {3}
• Espaço de amostra: {1, 2, 3, 4, 5, 6}
• Evento: {O resultado é par}={2, 4, 6}
slide 5
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Exemplo: identificando
o espaço amostral
Um experimento de probabilidade consiste em jogar
uma moeda e depois rolar um dado de seis lados.
Descreva o espaço amostral.
Solução:
Existem dois possíveis resultados quando se joga uma
moeda: cara (A) ou coroa (B). Para cada um deles, há
mais seis possíveis resultados quando se rola um dado:
1, 2, 3, 4, 5 ou 6. Um meio de listar resultados para
ações em sequência é usar um diagrama de árvore.
slide 6
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Solução: identificando
o espaço amostral
Diagrama de
árvore:
A1 A2 A3 A4 A5 A6
B1 B2 B3 B4 B5 B6
O espaço amostral possui 12 resultados:
{A1, A2, A3, A4, A5, A6, B1, B2, B3, B4, B5, B6}
slide 7
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Evento simples
Evento simples
• Um evento que consiste de um único resultado
 Ex.: “Tirar cara na moeda e rolar um 3” {A3}
• Um evento que consiste de mais de um resultado não
é um evento simples
 Ex.: “Tirar cara na moeda e rolar um número par”
{A2, A4, A6}
slide 8
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Exemplo: identificando
evento simples
Determine se o evento é simples ou não.
• Você rola um dado de seis lados. O evento B é rolar
pelo menos um 4
Solução:
Não é simples (o evento B tem três possíveis resultados:
4 ou 5 ou 6).
slide 9
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Princípio fundamental
da contagem
Princípio fundamental da contagem
• Se um evento pode ocorrer de m maneiras e um
segundo evento pode ocorrer de n maneiras, o
número de maneiras que os dois eventos podem
ocorrer em sequência é m*n
• Pode ser estendido para qualquer número de eventos
ocorrendo em sequência
slide 10
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Exemplo: princípio
fundamental da contagem
Você está comprando um carro novo. As possíveis montadoras,
tamanhos de carro e cores são listadas.
Montadoras: Ford, GM, Honda
Tamanho: compacto, médio
Cores: branco (B), vermelho (V), preto (P), amarelo (A)
De quantos modos diferentes você pode escolher uma
montadora, um tamanho de carro e uma cor? Use um diagrama
de árvore para verificar seus resultados.
slide 11
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Solução: princípio
fundamental da contagem
Há três escolhas de montadoras, dois tamanhos de carro e
quatro cores.
Usando o princípio fundamental da contagem:
3 ∙ 2 ∙ 4 = 24 maneiras
slide 12
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Tipos de probabilidade
Probabilidade clássica
• Cada resultado em uma amostragem é igualmente
provável
slide 13
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Exemplo: encontrando
probabilidades clássicas
Você rola um dado de seis lados. Encontre a probabilidade de
cada evento.
1. Evento A: rolar um 3
2. Evento B: rolar um 7
3. Evento C: rolar um número menor que 5
Solução:
Espaço amostral: {1, 2, 3, 4, 5, 6}
slide 14
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Solução: encontrando
probabilidades clássicas
slide 15
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Tipos de probabilidade
Probabilidade empírica (estatística)
• Baseado nas observações obtidas de experimentos de
probabilidade
• Frequência relativa de um evento
slide 16
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Exemplo: encontrando
probabilidade empírica
Uma empresa está conduzindo uma pesquisa on-line com indivíduos
selecionados aleatoriamente para determinar se o congestionamento no
trânsito é um problema em sua comunidade. Até agora, 320 pessoas
responderam à pesquisa. A distribuição de frequência mostra os
resultados. Qual é a probabilidade de que a próxima pessoa que
responda a essa pesquisa diga que o congestionamento é um problema
sério em sua comunidade?
Resposta
Número de vezes, f
Problema sério
123
Problema moderado
115
Não é problema
82
Σf = 320
slide 17
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Solução: encontrando
probabilidade empírica
Resposta
evento
Número de vezes, f
Problema sério
123
Problema moderado
115
Não é problema
82
frequência
Σf = 320
slide 18
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Lei dos grandes números
Lei dos grandes números
Conforme um experimento é repetido, a
probabilidade empírica de um evento se aproxima da
probabilidade teorética (real) do evento.
slide 19
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Tipos de probabilidade
Probabilidade subjetiva
• Intuição, palpites e estimativas
• Ex.: um médico pode achar que um paciente tem 90%
de chance de se recuperar completamente.
slide 20
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Exemplo: classificando
tipos de probabilidade
Classifique a afirmação como um exemplo de
probabilidade clássica, empírica ou subjetiva.
1. A probabilidade que você esteja casado aos 30
anos é 0,50.
Solução:
Probabilidade subjetiva (mais provavelmente um
palpite).
slide 21
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Classifique a afirmação como um exemplo de
probabilidade clássica, empírica ou subjetiva.
2. A probabilidade de um votante aleatório escolher
certo candidato é 0,45.
Solução:
Probabilidade empírica (mais provavelmente baseado
em uma pesquisa).
slide 22
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Classifique a sentença como um exemplo de
probabilidade clássica, empírica ou subjetiva.
3. A probabilidade de ganhar em uma rifa com 1.000
bilhetes comprando um bilhete é 1.
1000
Solução:
Probabilidade clássica (resultados igualmente prováveis).
slide 23
© 2010 Pearson Prentice Hall. Todos os direitos reservados.
Histórico do Histograma
André Michel Guerry nasceu em 1802 na França, era
um advogado e estudioso da estatística.
Os Histogramas foram apresentados pela primeira vez
por A. M. GUERRY, em 1833, para descrever sua
análise estatísticas sobre crimes contra a população
em Paris. Faleceu em 1866.
Histórico do Histograma
Vantagens do Histograma
• Trabalha com amostras e permite um menor
custo e tempo
• Determinamos de forma rápida qual o
comportamento da população
• Entender a população de uma forma clara e
objetiva.
Histograma
Ferramentas da Qualidade
Histograma
Na estatística
um histograma é uma
representação gráfica da distribuição de
frequências de uma massa de medições,
normalmente um gráfico de barras verticais.
CONCEITOS ESTATÍSTICOS VISTOS
1) POPULAÇÃO
2) AMOSTRA
3) PARÂMETRO
4) ESTATÍSTICA
5) NOMINAL, ORDINAL, INTERVALO, RAZÃO, PROPORÇÃO
6) FREQUENCIA
7) FREQUENCIA RELATIVA
8) FREQUENCIA ACUMULADA
9) MÉDIA ARITMÉTICA
10) MÉDIA PONDERADA
11) PROBABILIDADE
12) ESTRATIFICAÇÃO
13) MODA
CONCEITOS ESTATÍSTICOS
1) Classe Modal - é a classe ou intervalo, para dados classificados, que
aparece com maior frequência.
2) Amplitude de um Conjunto de Dados - é a diferença entre o maior
valor e o menor valor desse conjunto. Se os dados estiverem agrupados
em classes, a amplitude é a diferença entre o limite superior da última
classe e o limite inferior da primeira.
Para um intervalo do conjunto de dados de [a,b], onde x1= a e xn= b
CONCEITOS ESTATÍSTICOS
Desvio Médio ( d )- é a média aritmética do valor absoluto da diferença
entre cada valor e a média, no caso dos dados não classificados. No caso
dos dados classificados, tem que se entrar em conta com a frequência
absoluta de cada observação. [Fórmula]
Dados não classificados
Dados classificados
Desvio Padrão ( )- é a raiz quadrada positiva da variância. [Fórmula]
(com n = nº de observações da amostra)
CONCEITOS ESTATÍSTICOS
Variáveis Contínuas - são as variáveis que podem tomar qualquer valor de
um determinado intervalo.
Variáveis Discretas - são as variáveis que podem tomar um número finito ou
uma infinidade numerável de valores.
Variáveis Qualitativas - o mesmo que Atributos Qualitativos.
Variáveis Quantitativas - o mesmo que Atributos Quantitativos.
nº de observações
da amostra) avaliar o grau de dispersão dos
Variância ( )-(com
é an =medida
que permite
valor da variável em relação à média.
CONCEITOS ESTATÍSTICOS
CONCEITOS ESTATÍSTICOS
Variação e Distribuição
Se pudéssemos coletar dados de um processo no qual todos os fatores
(homem, máquina, matéria-prima, método, etc.) fossem perfeitamente
constantes, todos os dados teriam o mesmo valor.
Entretanto, na realidade, é impossível manter todos os fatores constantes todo
o tempo.
A rigor, mesmo alguns fatores que julgamos sejam constantes, não são
perfeitamente constantes.
É inevitável que os valores de um certo conjunto de dados apresentem alguma
variação.
Os valores não são sempre os mesmos, mas isto não significa que sejam
determinados de maneira desordenada.
Embora os valores estejam sempre mudando, eles são regidos por uma certa
regra e, nesta situação, dizemos que seguem uma certa distribuição.
Populações e Amostras
No controle da qualidade, tentamos descobrir fatos através da coleta
de dados e, então, tomamos a ação necessária baseados naqueles
fatos.
Os dados não são coletados como um objetivo final em si, mas como
um meio para descobrir os fatos que estão por trás dos dados.
Por exemplo, considere urna inspeção por amostragem. Tomamos
uma amostra de um lote, executamos medições nela e, então,
decidimos se devemos aceitar todo o lote ou não. Nossa preocupação
aqui não é a amostra em si, mas a qualidade de todo o lote.
Como outro exemplo, considere o controle _de um processo de
fabricação usando um gráfico de controle x-R .
O propósito não é determinar as características da amostra coletada
para a construção do gráfico de controle x-R, mas descobrir em que
estado se encontra o processo.
Populações e Amostras
A totalidade dos itens considerados é chamada de população.
No primeiro exemplo, a população é o lote e, no segundo, é o
processo.
Algumas pessoas acham difícil considerar um "processo" como uma
"população", porque enquanto um "lote" é um grupo de objetos
individuais finitos, um "processo" em si não é absolutamente um
produto, mas é composto dos 5M's (homem, máquina, material,
método e medição).
Quando voltamos nossa atenção h função de fabricar produtos,
reconhecemos que, inequivocamente, o processo produz um conjunto
de produtos. Além disso, a quantidade de produtos é infinita a menos
que o "processo" pare de produzi-los e, por esta razão, consideramolo como uma população infinita.
Populações e Amostras
Um ou mais itens retirados de uma população com a intenção
de prover informações sobre ela, são chamados de amostra.
Uma vez que uma amostra é utilizada para estimar as
características de toda a população. ela deve ser escolhida de
tal forma a refletir as características da população.
Um método de amostragem comumente usado é escolher um
membro qualquer da população com igual probabilidade.
Este método é chamado de amostragem aleatória, e uma
amostra retirada mediante este tipo de amostragem é chamada
de amostra aleatória.
Populações e Amostras
Populações e Amostras
Dados obtidos de uma amostra servem como base para uma
decisão sobre a população.
Quanto maior o tamanho da amostra, mais informação obtemos
sobre a população. Porém, um aumento do tamanho da amostra
também implica um aumento da quantidade de dados, e isso
torna difícil compreender a população a partir destes, mesmo
quando estão organizados em tabelas.
Em tal caso, precisamos de um método que nos possibilite
conhecer a população num rápido exame. Um histograma atende
às nossas necessidades. Por meio da organização de muitos
dados num histograma, podemos conhecer a população de
maneira objetiva.
Análise de melhoria de processo
Muitas vezes somente a quantidade de dados não é
suficiente para se tomar uma decisão.
Em muitos casos preciso observar a forma como os
dados estão distribuídos ao longo de um intervalo préestabelecido.
O histograma mostra de forma resumida, o número de
vezes que o valor de uma variável ocorre dentro de
intervalos especificados.
Distribuição de frequência
Distribuição de
frequência
 Uma tabela que mostra
classes ou intervalos Tamanho da
de dados com uma
classe 6 – 1 = 5
contagem do número de
entradas em cada classe
 A frequência, f, de
uma classe é o número
de entradas de dados na
classe
Classe Frequência,
f
1–5
5
6 – 10
8
11 – 15
6
16 – 20
8
21 – 25
5
26 – 30
4
Limite inferior da
classe
Limite superior da
classe
Construindo uma distribuição de
frequência
1. Decida o número de classes.

Geralmente entre 5 e 20; do contrário, pode ser difícil
detectar padrões
2. Encontre o tamanho da classe.

Determine a variação dos dados

Divida a variação pelo número de classes

Arredonde para cima para o próximo número
conveniente
3. Encontre os limites da classe.
 Você pode usar a entrada de menor valor como o limite
inferior da primeira classe
 Encontre os limites inferiores remanescentes
(adicione o tamanho da classe ao limite inferior da
classe precedente)
 Encontre o limite superior da primeira classe. Lembrese de que as classes não podem ter limites iguais
 Encontre os limites superiores remanescentes
4. Faça um registro para cada entrada de dados na
fileira da classe apropriada.
5. Conte os registros para encontrar a frequência total f
para cada classe.
Exemplo: construindo uma
distribuição de frequência
A amostra seguinte lista o número de minutos que 50
usuários da internet passaram conectados durante a
sessão mais recente. Construa uma distribuição de
frequência para as sete classes.
50 40 41 17 11 7 22 44 28 21 19 23 37 51 54 42 86
41 78 56 72 56 17 7 69 30 80 56 29 33 46 31 39 20
18 29 34 59 73 77 36 39 30 62 54 67 39 31 53 44
Solução: construindo uma
distribuição de frequência
50 40 41 17 11 7 22 44 28 21 19 23 37 51 54 42 86
41 78 56 72 56 17 7 69 30 80 56 29 33 46 31 39 20
18 29 34 59 73 77 36 39 30 62 54 67 39 31 53 44
Número de classes = 7 (dados)
2. Encontre o tamanho da classe
1.
max  min 86  7

 11.29
#classes
7
Arredondando para
cima: 12
3. Use 7 (valor mínimo)
como o primeiro limite
mínimo. Adicione o
tamanho da classe, 12,
para definir o limite
mínimo da próxima
classe.
7 + 12 = 19
Encontre os limites
mínimos restantes.
Limite Limite
mínimo máximo
Tamanho
da classe =
12
7
19
31
43
55
67
79
O limite máximo da
Limite
primeira classe é 18 (um a
menos que o limite mínimo mínimo
7
da segunda classe).
19
Some o tamanho da classe,
31
12, para definir o limite
máximo da próxima classe.
43
18 + 12 = 30
55
Encontre os limites máximos
67
restantes.
79
Limite
máximo
18
30
42
54
66
78
90
Tamanho
da classe =
12
4. Faça um registro para cada entrada de dado na fileira
da classe apropriada.
5. Conte os registros para encontrar a frequência total f
para cada classe.
Classe
7 – 18
Registro
Frequência, f
IIII I
6
19 – 30
IIII IIII
10
31 – 42
IIII IIII III
13
43 – 54
IIII III
8
55 – 66
IIII
5
67 – 78
IIII I
6
79 – 90
II
2
Σf = 50
Determinando o ponto médio
Ponto médio de uma classe
(Limite mínimo da classe) + (Limite máximo da classe)
2
Classe
Ponto médio
Frequência, f
7 – 18
7  18
 12.5
2
19 – 30
19  30
 24.5
2
10
31 – 42
31  42
 36.5
2
13
6
Tamanho da classe = 12
Determinando a frequência relativa
Frequência relativa de uma classe
 Porção da porcentagem dos dados que se encaixa em
um classe em particular
•
Frequência da classe
Frequência relativa =
Tamanho da amostragem
Classe
Frequência, f
7 – 18
6
19 – 30
10
31 – 42
13
Frequência relativa
6
 0.12
50
10
 0.20
50
13
 0.26
50

f
n
Frequência acumulada de uma classe
A soma das frequências daquela classe e de todas as
classes anteriores.
Larson/Farber 4th ed.
Classe
Frequência, f
7 – 18
6
6
19 – 30
+ 10
16
31 – 42
+ 13
29
54
Frequência acumulada
Distribuição de frequência expandida
Classe
Frequência, f
Ponto
médio
7 – 18
6
12.5
0.12
6
19 – 30
10
24.5
0.20
16
31 – 42
13
36.5
0.26
29
43 – 54
8
48.5
0.16
37
55 – 66
5
60.5
0.10
42
67 – 78
6
72.5
0.12
48
79 – 90
2
84.5
0.04
50
Σf = 50
Frequência
relativa
Frequência
acumulada
f
 1
n
Gráficos de distribuição de frequência
Frequência
Histograma de frequência
 Um gráfico de barras que representa a distribuição da frequência
 O eixo horizontal é quantitativo e mede os valores dos dados
 O eixo vertical mede as frequências das classes
 Barras consecutivas precisam se tocar
Valores dos
dados
Fronteiras de classes
 Os números que separam as classes sem formar
espaços entre elas
• A distância do limite superior da
primeira classe para o limite
inferior da segunda é 19 – 18 = 1
• A metade dessa distância é 0,5
• Fronteira inferior da
primeira
classe = 7 – 0.5 = 6.5
• Fronteira superior da
primeira classe = 18 + 0.5 =
18.5
Classe
7 – 18
Fronteiras Frequência,
de classes
f
6.5 – 18.5
6
19 – 30
10
31 – 42
13
Classe
7 – 18
19 – 30
31 – 42
43 – 54
55 – 66
67 – 78
79 – 90
Fronteiras de Frequência,
classes
f
6.5 – 18.5
6
18.5 – 30.5
10
30.5 – 42.5
13
42.5 – 54.5
8
54.5 – 66.5
5
66.5 – 78.5
6
78.5 – 90.5
2
Exemplo: histograma de frequência
Construa um histograma de frequência para a
distribuição da frequência do uso da internet.
Classe
Fronteiras de
classes
Ponto
médio
Frequência,
f
7 – 18
6.5 – 18.5
12.5
6
19 – 30
18.5 – 30.5
24.5
10
31 – 42
30.5 – 42.5
36.5
13
43 – 54
42.5 – 54.5
48.5
8
55 – 66
54.5 – 66.5
60.5
5
67 – 78
66.5 – 78.5
72.5
6
79 – 90
78.5 – 90.5
84.5
2
Solução: histograma de
frequência (usando pontos médios)
Frequência
Uso de Internet
Tempo on-line (em minutos)
Solução: histograma de
frequência (usando fronteiras de classes)
Frequência
Uso de Internet
6.5
18.5
30.5
42.5
54.5
66.5
78.5
90.5
Tempo on-line (em minutos)
É visível que mais da metade dos assinantes passaram entre 19 e
54 minutos na Internet em sua sessão mais recente.
Gráficos de distribuição de frequência
Frequência
relativa
Histograma de frequência relativa
 Tem o mesmo formato e eixo horizontal que o
histograma de frequência correspondente
 O eixo vertical mede as frequências relativas e não as
frequências
Valores dos
dados
Exemplo: histograma de frequência relativa
Construa um histograma de frequência relativa para a
distribuição da frequência do uso de Internet.
Classe
Fronteiras de
classes
Frequência, Frequênci
f
a relativa
7 – 18
6.5 – 18.5
6
0.12
19 – 30
18.5 – 30.5
10
0.20
31 – 42
30.5 – 42.5
13
0.26
43 – 54
42.5 – 54.5
8
0.16
55 – 66
54.5 – 66.5
5
0.10
67 – 78
66.5 – 78.5
6
0.12
79 – 90
78.5 – 90.5
2
0.04
Solução: histograma de frequência relativa
Frequência
Uso de Internet
6.5
18.5
30.5
42.5
54.5
66.5
78.5
90.5
Tempo on-line (em minutos)
A partir do gráfico, pode-se perceber que 20% dos assinantes
de Internet passaram entre 18,5 minutos e 30,5 minutos
conectados.
Análise de melhoria de processo
Como fazer um Histograma
•Passo 1 – coleta de dados
É aconselhável que o número de dados (n)
seja superior a 30 para que tenhamos um
histograma representativo.
Análise de melhoria de processo
•Passo 1 – coleta de dados
n = 40
Análise de melhoria de processo
•Passo 2 – escolha o número de classes (k)
Não existe uma regra universal para a escolha do número de
classes em um histograma. A sugestão é que seja usada a
seguinte tabela:
Análise e melhoria de processos
•Passo 2 – escolha o número de classes (k)
Não existe uma regra universal para a escolha do
número de classes em um histograma. A
sugestão é que seja usada a seguinte tabela:
PARA n
30 até 50
k
5 até 7
51 até 100
101 até 250
Mais que 250
6 até 10
7 até 12
10 até 20
Análise e melhoria de processos
•Passo 1 – coleta de dados
Peso em Kg
48,9
49,3
49,5
49,7
49,3
49,8
49,1
49,6
49,6
48,9
49,3
49,6
49,5
48,8
49,7
49,2
49,3
49,1
49,2
49,0
49,7
49,4
49,1
49,9
49,3
48,9
50,1
49,6
49,1
49,3
50,0
49,4
49,8
49,4
49,4
49,4
49,6
48,8
49,1
49,5
n = 40
k=5
Análise e melhoria de processos
•Passo 3 – identifique o valor mínimo e
máximo dos dados.
MÁX = 50,1
MÍN = 48,8
•Passo 4 – calcule a amplitude dos dados (R)
R = MÁX - MÍN
R = 50,1 – 48,8 = 1,3
Análise e melhoria de processos
•Passo 5 – calcule o comprimento de cada intervalo
no histograma (h)
h = R/k
h = 1,3/5
h = 0,26
Análise e melhoria de processos
•Passo 6 – arredonde o valor de h
Deve ser arredondado para cima. O bom senso deve
prevalecer.
h ≈ 0,3
•Passo 7 – determine as classes a partir do menor valor.
Nota: em cada classe o menor valor pertence a ela, porém,
o maior valor não.
Análise e melhoria de processos
•Passo 7 – determine as classes a partir do menor valor.
48,8 ├ 49,1
48,8 + 0,3 = 49,1
49,1 ├ 49,4
49,1 + 0,3 = 49,4
49,4 ├ 49,7
49,4 + 0,3 = 49,7
49,7 ├ 50,0
49,7 + 0,3 = 50,0
50,0 ├ 50,3
50,0 + 0,3 = 50,3
Análise e melhoria de processos
•Passo 8 – construa uma tabela de distribuição de freqüências.
Limites do intervalo
Freqüência de
ocorrência
48,8 ├ 49,1
6
49,1 ├ 49,4
13
49,4 ├ 49,7
13
49,7 ├ 50,0
6
50,0 ├ 50,3
2
Análise e melhoria de processos
•Passo 9 – desenhe o histograma.
14
12
10
8
6
4
2
0
48,8 ├ 49,1
49,1 ├ 49,4
49,4 ├ 49,7
49,7 ├ 50,0
50,0 ├ 50,3
Como Construir Histogramas
Exemplo prático de fixação
Para investigar a distribuição dos diâmetros de eixos
de aço produzidos em um processo de usinagem, os
diâmetros de 90 eixos foram medidos conforme
mostra a Tabela a seguir.
Vamos construir um histograma para a tomada de
decisão usando estes dados.
ETAPA 1 – AMPLITUDE
PROCEDIMENTO Calcular a ampíitude (R)
Obtenha o maior e o menor dos valores observados e calcule R.
R = (O maior valor observado) - (o menor valor observado)
O maior e o menor dos valores observados podem ser facilmente obtidos da
seguinte maneira:
Obtenha o máximo e o mínimo dos valores de cada linha da tabela de
observações, e depois tome o maior dos valores máximos e o menor dos
valores mínimos. Estes serão o máximo e o mínimo de todos os valores
observados.
EXEMPLO
R foi obtida a partir do maior e do menor valores observados. (Veja Tabela )
O maior valor = 2,545
(-)
O menor valor z 2,502
Portanto,
R = 2,545 - 2,502 = 0,043
ETAPA 2 – INTERVALO DE CLASSE
O intervalo de classe é determinado de forma que a amplitude, que
compreende o maior e o menor dos valores, seja dividida em intervalos de
mesmo tamanho. Para obter o tamanho dos intervalos, divida R por l, 2 ou 5
(ou 10; 20; 50; 0,l; 02; 0,5; etc.) de forma a obter de 5 a 20 intervalos de
classe de tamanho igual. Quando houver duas possibilidades, use o tamanho
de intervalo menor se o número de valores observados for maior ou igual a
100, e o tamanho de intervalo maior se houver 99 ou menos valores
observados.
EXEMPLO
0,043 + 0,002 = 21,5 e adotamos 22, pelo arredondamento para cima até o
número inteiro mais próximo.
0,043 + 0,005 = 8,6 e adotamos 9, pelo arredondamento para cima até o
número inteiro mais próximo.
0,043 + 0,010 = 4,3 e adotamos 4, pelo arredondamento para baixo até o
número inteiro mais próximo.
Neste caso, o intervalo de classe é determinado como 0,005, pois isso resulta
numa quantidade de intervalos entre 5 e 20.
Etapa 3 Preparar o formulário da tabela de
frequência
PROCEDIMENTO
Prepare um formulário como o da Tabela, no qual possam ser
registrados as classes, o ponto médio, as marcas
de frequência, frequência, etc.
EXEMPLO
Prepare uma tabela conforme mostra a Tabela.
Etapa 4 Determinar os limites das ciasses
PROCEDIMENTO
1. Determine os limites dos intervalos, de forma que englobem o menor e o
maior dos valores registrados, e anote-os na tabela de frequência.
2. Determine, primeiro, o limite inferior da primeira classe e adicione a este o
tamanho do intervalo para obter o limite entre a primeira e a segunda
classe. Quando fizer isso, assegure-se de que a primeira classe contém o
menor valor observado e que os valores dos limites tenham uma casa
decimal a mais do que a precisão dos valores medidos.
3. Depois, adicione sucessivamente o tamanho do intervalo ao valor do limite
anterior para obter o segundo limite, o terceiro, e assim por diante, e
verifique se a última classe inclui o maior valor observado.
EXEMPLO
Os limites da primeira classe devem ser determinados como 2,5005 e 2,5055
de forma que a classe inclua o menor valor 2,502; os limites da segunda classe
devem ser determinados como 2,5055 e 2,5105, e assim por diante.
Registre esses limites numa tabela de frequência. (Veja Tabela a seguir)
Etapa 5 Calcular o ponto médio da classe
PROCEDIMENTO
Usando a equação seguinte, calcule o ponto médio das classes,
e anote-os na tabela de frequência.
Ponto médio da primeira classe:
Soma dos limites superior e inferior da primeira classe
2
Ponto médio da primeira classe
2,5005 + 2,5055 = 2,503
2
Etapa 6 Obter as freqüências
Leia os valores observados um por um e registre as frequências
obtidas em cada classe usando marcas de contagem em grupos
de 5, como segue:
Como construir o gráfico histograma
ETAPA 1
Em uma folha de papel quadriculado, marque o eixo horizontal com uma
escala. É melhor que a escala não seja baseada nos limites de intervalo das
classes, e sim na unidade de medida dos dados, 10 gramas correspondendo a
10 mm, por exemplo. Isto toma-a conveniente para fazer comparações entre
vários histogramas que descrevem fatores e características semelhantes, bem
como com especificações (padrões).
Deixe um espaço aproximadamente igual ao intervalo de classe em cada
extremidade do eixo horizontal, antes da primeira e após a última classe.
ETAPA 2
Marque o eixo vertical do lado esquerdo com uma escala de frequência e, se
necessário, trace o eixo vertical do lado direito e marque-o com uma escala de
frequência relativa.
A altura da classe com a frequência máxima deveria ser de 0.5 a 2,O vezes a
distância entre os valores máximo e mínimo do eixo horizontal .
Como construir o gráfico histograma
Etapa 3
Marque os valores dos limites das classes no eixo horizontal.
Etapa 4
Usando o intervalo de classe como base, desenhe um retângulo
cuja altura corresponda à frequência daquela classe.
Etapa 5
Trace uma linha no histograma para representar a média e, se for o caso, trace
também os limites da especificação.
Etapa 6
Numa área em branco do histograma, anote o histórico dos dados (o período _
em que os dados foram coletados, etc.), a quantidade de dados (n), a média x
e o desvio-padrão s (veja Figura 5.2).
GRÁFICO HISTOGRAMA
Como Interpretar Histogramas
Tipos de Histograma
É possível obter informações úteis sobre a população pela análise da forma
do histograma. As seguintes formas s3o típicas, e podemos utilizá-las como
modelos para a análise de um processo. Tipos: geral, pente, assimétrico
positivo, abrupto à esquerda, achatado, picos duplos e pico isolado.
Como Interpretar Histogramas
a) Tipo geral (simétrico ou em forma de sino)
Forma:
O valor médio do histograma está no meio da amplitude dos dados.
A frequência é mais alta no meio e toma-se gradualmente mais baixa
na direção dos extremos. A forma é simétrica.
Nota: Esta é a forma que ocorre mais frequentemente.
Como Interpretar Histogramas
a) Tipo pente (tipo multi-modal)
Forma:
Várias classes têm, como vizinhas, classes com menor
frequência.
Nota:
Esta forma ocorre quando a quantidade de dados incluídos na
classe varia de classe para classe ou quando existe uma
tendência particular no modo como os dados são
arredondados.
Como Interpretar Histogramas
Tipo assimétrico positivo (tipo assimétrico negativo)
Forma:
O valor médio do histograma fica localizado à esquerda (direita) do
centro da amplitude. A frequência decresce de modo um tanto abrupto
em direção à esquerda (direita), porém de modo suave em direção à
direita (esquerda). É assimétrica.
Nota:
Esta forma ocorre quando o limite inferior (superior) é controlado,
ou teoricamente, ou por um valor de especificação, ou quando valores
menores (maiores) do que um certo valor não ocorrem.
Como Interpretar Histogramas
Tipo abrupto à esquerda (tipo abrupto à direita)
Forma:
O valor médio do histograma fica localizado bem à esquerda (direita)
do centro da amplitude. A frequência decresce abruptamente à esquerda
(direita), e suavemente em direção à direita (esquerda). É assimétrica.
Nota:
Esta é uma forma que ocorre frequentemente quando é feita uma
inspeção separadora 100% por causa da baixa capacidade do processo,
e também quando a assimetria positiva (negativa) se toma ainda mais
extrema.
Como Interpretar Histogramas
Tipo achatado
Forma:
As frequências das classes formam um achatamento porque as classes
possuem mais ou menos a mesma frequência, exceto aquelas das
extremidades.
Nota:
Esta forma ocorre com a mistura de várias distribuições que têm
diferentes médias.
Como Interpretar Histogramas
Tipo picos duplos (tipo bimodal)
Forma:
A frequência é baixa próximo ao meio da amplitude de dados e existe
um pico em cada lado.
Nota:
Esta forma ocorre quando duas distribuições, com médias muito
diferentes, são misturadas.
Como Interpretar Histogramas
Tipo pico isolado
Forma:
Num histograma do tipo geral existe mais um pequeno pico isolado.
Nota:
Esta é uma forma que surge quando há uma pequena inclusão de dados
provenientes de uma distribuição diferente, como nos casos de
anormalidade de processo, erro de medição ou inclusão de dados de um
processo diferente..
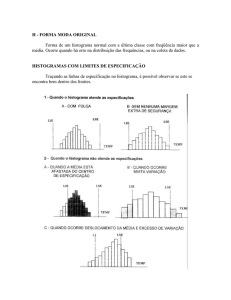
Comparação de Histogramas com Limites
de Especificação
Se houver uma especificação, trace as linhas dos limites
da especificação no histograma, para comparar a
distribuição com a especificação.
Depois veja se o histograma está localizado bem dentro
dos limites.
Cinco casos típicos, como na Figura 5.4, são descritos a
seguir. Use-os
como uma referência para avaliar a população.
Comparação de Histogramas com Limites
de Especificação
Quando o histograma atende à especificação
a) Como o histograma atende à especificação com folga, tudo o
que se precisa é manter a atual situação.
b) A especificação é atendida mas não existe nenhuma margem
extra.
Portanto, é importante reduzir um pouco o grau da variação.
Comparação de Histogramas com Limites
de Especificação
Quando o histograma não atende à especificação
c) É necessário agir para trazer a média mais próxima ao centro
da especificação.
d) São necessárias ações para reduzir a variação.
e) Tanto as ações descritas em c) como em d) são necessárias.
Estratificação de Histogramas
Quando os valores observados são divididos em duas ou mais
subpopulações, conforme as condições existentes na coleta de
dados, tais subpopulações são chamadas de estratos e a divisão
de dados em estratos é chamada de estratificação.
Os valores observados sempre trazem alguma variação. Por isso,
quando os dados são estratificados conforme os fatores suspeitos
de gerar a variação, as causas de variação tornam-se mais
facilmente detectáveis.
Este método pode ser usado eficazmente para aumentar a
qualidade de produto, pela redução da variação e ajuste da média
do processo.
A estratificação é geralmente feita conforme os materiais, as
máquinas, as condições de operação e os trabalhadores.