Proporcionalidade directa

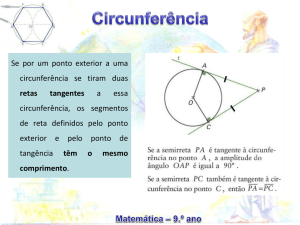
Circunferência é o conjunto dos pontos equidistantes de um ponto (centro)
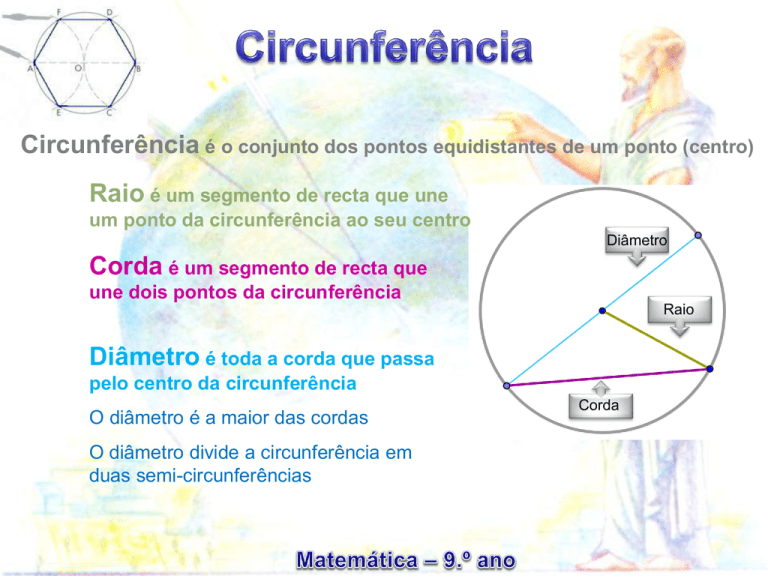
Raio é um segmento de recta que une
um ponto da circunferência ao seu centro
Diâmetro
Corda é um segmento de recta que
une dois pontos da circunferência
Raio
Diâmetro é toda a corda que passa
pelo centro da circunferência
O diâmetro é a maior das cordas
O diâmetro divide a circunferência em
duas semi-circunferências
Corda
Ângulo ao Centro e Arco de Circunferência
A
c
Um ângulo formado por dois raios designa-se
ângulo ao centro (o vértice do ângulo coincide
com o centro da circunferência)
B
Qualquer porção da circunferência determinada
por dois dos seus pontos, que são os extremos
do arco designa-se Arco de circunferência.
Nota – Quando falamos em arco, sem nada
acrescentar referimo-nos ao arco menor
AB
 Ao ângulo ao centro ACB corresponde a
corda [AB] e o arco [AB] e vice-versa.
 Numa circunferência, qualquer ângulo que
não seja ao centro diz-se excêntrico.
Pág.12 – exercício 1
Observa a circunferência de centro O da figura:
a)
Identifica quatro ângulos ao centro. AOB ; BOC ; COD e EOD
b)
Indica dois pares de ângulos ao BOC  FOE
centro geometricamente iguais.
c)
Classifica quanto aos lados o triângulo
[EOD].
Triângulo isósceles
AOB  EOD
A
D
Numa circunferência:
C
- a cada ângulo ao centro
corresponde um arco e vice-versa
- A arcos iguais correspondem
cordas e ângulos ao centro iguais
- A ângulos ao centro iguais
B
E
F
G
correspondem arcos e cordas iguais
- A cordas iguais correspondem
arcos e ângulos ao centro iguais
- A amplitude de um arco é igual à amplitude
do ângulo ao centro correspondente
H
C
I
Pág.13 – exercício 3
Observa a figura onde [MT]  [EA].
Prova que MA  AT  TE  EM
Resposta:
MA  AT  TE  EM
Esta afirmação é verdadeira porque se
trata dos comprimentos dos lados de um
quadrado, pois como [MT] e [EA] são
diâmetros
representam
da
as
circunferência,
diagonais
quadrado, por serem iguais.
de
um
Pág.13 – exercício 4
Na figura abaixo, [AD] é um diâmetro da circunferência de

centro O, AOB  60º e OC é a bissectriz do ângulo BOD.
a) Calcula BOC e COD. BOC  60º; COD  60º
b) Que podemos concluir em relação a
AB , BC , CD. Porquê? A amplitude dos
arcos é 60º porque a amplitude dos ângulos ao
centro correspondentes também é 60º.
c) E em relação a AB , BC e CD. Porquê?
P  d 
Os comprimentos das cordas são iguais
porque a arcos e ângulos ao centro iguais
correspondem cordas iguais
AO  2 cm , calcula o comprimento do arco AB.
2
P
4
2
Se AO  2cm, r  2cm e d  4cm log o AB 


cm.
6
6 2 3
d) Supondo que
Pág.23 – exercício 1 a) e c)
Observa as figuras e determina, em cada caso, os valores de x e y.
a)
Ângulos verticalmente opostos
x
y  30º e x  30º
y
c)
x+30º 2x - 10º
x  30º  2 x  10º 
 x  2 x  10º 30º 
 1x  40º 
 x  40º
Ângulo inscrito
F
Um ângulo formado por duas cordas designase
c
E
ângulo inscrito
(o vértice do ângulo
coincide com um ponto da circunferência)
D
80º
A amplitude de um ângulo inscrito é igual
a
metade
da
amplitude
do
arco
compreendido entre os seus lados
O ângulo ao centro tem de amplitude 80º, logo a
amplitude do arco correspondente também é 80º, o
que significa que a amplitude do ângulo inscrito é
igual a metade da do arco correspondente (80º/2=40º).
Pág.15 – exercício 6
Observa a figura e indica:
a) Um ângulo ao centro;
AOC
b) Um ângulo inscrito;
ABC
c) Um arco de circunferência;
AB
d) Um raio de circunferência;
OC 
e) Uma corda da circunferência.
 AB
Pág.15 – exercício 7
Considera a circunferência de centro O.
a) [AB] e [DC] são diâmetros. Porquê?
Porque são cordas que passam pelo centro.
b) Se
b1)
AOD  34º , calcula:
COB
b2)
ABD
b3) DB
b4) B AD
b5)
ADB
ADB 
360º 146º 34º 180º

 90º
2
2
COB  34º (ângulos verticalmente opostos)
34º
ABD 
 17º
2
DB  180º 34º  146º
180º 34º 146º

 73º
2
2
( ângulos de 1 isósceles )
146º
B AD 
 73º
2
B AD 
( ângulo inscrito correspondente a BD que é 146º )
Abre agora o programa Geogebra, no teu
computador, e verifica o exercício anterior
começando por:
 traçar uma recta (com 2 pontos);
 desenhar uma circunferência (centro sobre um ponto e
raio no outro);
 marcar os pontos A e B;
marcar o ângulo AOD de 34º e os pontos D e C;
 marcar a corda DB;
verificar todos os resultados.
Ângulo inscrito
Propriedades:
 Os ângulos inscritos no mesmo arco de
circunferência são geometricamente iguais.
 Qualquer ângulo inscrito numa semicircunferência é recto.
Pág.17 – exercício 12
O triângulo [MAR] representado na figura é rectângulo em A e os seus
três vértices pertencem à circunferência.
Sabendo que MA  QM e que M RA  30º
calcula QAR .
MA  30º 2  MA  60º log o QM  60º
M AR  90º (ângulo inscrito numa semi  circunferência)
então MQR  180º
MQR  MQ
180º 60º
 QAR 

2
2
120
 QAR 
 QAR  60º
2
QAR 
Abre novamente o programa Geogebra e
verifica o exercício anterior começando por:
 traçar uma recta com dois pontos;
 desenhar uma circunferência (centro sobre um ponto e raio
no outro);
 marcar os pontos M e R;
 traçar o ângulo MRA de 30º;
 marcar o ponto A e a corda [MA];
 verificar que o ângulo MAR é 90º;
 traçar uma recta perpendicular a MR e marcar o
ponto Q;
 verificar todos os resultados.
Eixo de simetria de uma circunferência
Qualquer recta que passe pelo centro de uma
circunferência é eixo de simetria da circunferência.
Qualquer recta que passe pelo centro de uma circunferência
divide ao meio as cordas que lhe são perpendiculares, assim
como os ângulos ao centro e os arcos correspondentes.
Numa circunferência, arcos e
cordas compreendidos entre
cordas paralelas são
geometricamente iguais.
tangente
A tangente a uma circunferência
é perpendicular à recta que
90º
passa pelo centro e pelo ponto
de tangência.
Pág. 21
a)
ex.16
b)
ponto de
tangência
Pág. 21
a)
b)
ex.17
c)
Polígonos
Polígono
é o conjunto de pontos do plano limitado por uma linha
fechada, formada por segmentos de recta unidos pelas extremidades.
Polígono
Não Polígono
Os polígonos podem ser côncavos ou convexos.
Côncavo
Convexo
Polígonos
Polígono regular
Um polígono regular é todo o polígono convexo com as seguintes
características:
todos os seus lados têm a mesma
medida (são congruentes);
todos os seus ângulos internos têm
a mesma amplitude (são congruentes).
Diagonal de um Polígono
Diagonal de um polígono é qualquer
segmento de recta cujos extremos são
vértices não consecutivos do polígono.
Polígonos Regulares
Polígono
N.º Lados
Ângulo ao
Centro
Ângulo
Interno
Triângulo
equilátero
3
120º
60º
Quadrado
4
90º
90º
Pentágono
5
72º
108º
Hexágono
6
60º
120º
...
...
...
...
...
N
360º/N
= 180 - Ângulo
ao centro
Polígonos
Concluímos que:
A soma das amplitudes dos ângulos internos de um polígono
(convexo) de n lados é igual a (n-2)  180º.
triângulo
Si = (3 - 2)  180º =
= 1  180º =
= 180º
Hexágono
Pentágono
Si = (5 - 2)  180º =
= 3  180º =
= 540º
Si = (6 - 2)  180º =
= 4  180º =
= 720º
Polígonos
Concluímos que:
Num polígono convexo, qualquer que
seja o número de lados, a soma dos
ângulos externos é sempre 360º.
Polígonos inscritos numa circunferência
Polígono
N.º lados
N.º triângulos
Soma dos ângulos
internos
Triângulo
3
1
180º
Quadrilátero
4
2
2 × 180º = 360º
Pentágono
5
3
3 × 180º = 540º
Hexágono
6
4
4 × 180º = 720º
Heptágono
7
?
?
Octagono
8
?
?
Polígonos
Concluímos que:
Um polígono diz-se inscrito numa circunferência se esta contém todos os
seus vértices. A circunferência diz-se circunscrita ao polígono.
360º
DOC 
 72º
5
A amplitude do ângulo ao centro correspondente ao lado de um
polígono regular de n lados é 360º
n
Polígonos Regulares
Polígono
N.º Lados
Ângulo ao
Centro (Ac)
Ângulo
Interno (Ai)
Triângulo
equilátero
3
120º
60º
Quadrado
4
90º
90º
Pentágono
5
72º
108º
Hexágono
6
60º
120º
...
...
...
...
...
N
Ac = 360º/N
Ai = 180 - Ac
Polígonos
Página 31 – ex. 2 a)
(n  2) 180º  720º 
 180º n  360º  720º 
 180º n  720º 360º 
1080º
n

180º
n6
R : O polígono é um hexágono.
Página 31 – ex. 3
Si  (5  2) 180º 
 Si  3 180º 
 Si  540º
540º
 108º
5
R : O ângulo int erno é 108º.
ângulo int erno 
5n  360º 
360º
n

5
 n  72º
R : O ângulo externo é 72º.
Polígonos
Página 31 – ex. 6
Si  (n  2) 180º 
 Si  (6  2) 180º 
 Si  4 180º 
 Si  720º
Se Si  720º então
3 x  x  20º  x  30º 70º  720º 
 5 x  720º 20º 30º 70º 
600
x
 x  120º
5
R : O valor de x é 120º.
Página 31 – ex. 7
a) 360º 60º  6
R : O polígono é um hexágono regular.
b) 360º 110º  3
R : O polígono é um triângulo regular.
c) 360º 36º  10
R : O polígono é um decágono regular.
d ) 360º 90º  4
R : O polígono é um quadrado.
Polígonos
Como se pode determinar a área de um polígono
regular qualquer?
[ABCDE] é um pentágono regular inscrito na circunferência.
Dividimos o pentágono em cinco triângulos
isósceles geometricamente iguais.
Chama-se apótema de um polígono regular
ao segmento de recta que une o centro do
polígono com o ponto médio de qualquer um
dos lados.
h
o apótema do pentágono coincide com a altura de cada triângulo.
Polígonos
A área do polígono regular [ABCDE] pode ser obtida multiplicando por 5 a área
de um dos triângulos em que dividimos o pentágono.
A ABCDE  5  A
 AOB
ap
l
lado do pentágono.
Logo,
A ABCDE
A
 AOB
 ap
 5
2
 ap

2
Polígonos
A ABCDE
ap
5 
2
representa o perímetro do pentágono
A ABCDE
A ABCDE
ap
 P
2
P
  ap
2
De modo análogo prova-se que:
A poligono regular
P
  ap
2
P = perímetro do polígono
ap = apótema de um polígono
Polígonos
Página 33
ex. 24
P  12cm  8  96cm
96  8
A

2
768
 A

2
 A  384cm 2
ex. 25
c 2  h 2  c 2  c 2  102  52 
 c 2  100  25  c  75 cm
P  10 cm  6  60 cm
Apótema
60  75
A

2
 A  30 75 cm2
ex. 26
A
160  20
3200
 A
 A  1600 cm 2
2
2
A poligono regular
P
  ap
2
Chama-se ISOMETRIA a uma transformação geométrica em que
são conservados os comprimentos dos segmentos de recta e as
amplitudes dos ângulos
-Translação
Transforma uma figura F noutra figura F’ (imagem de F) tendo
como referência um vector
-Reflexão
Transforma uma figura F noutra figura F’ (imagem de F)
conhecendo um eixo (recta) de simetria
-Rotação
Transforma uma figura F noutra figura F’ (imagem de F) tendo um
centro de rotação (ponto) e a amplitude (ângulo) da rotação
Simetria
Intuitivamente, todos nós sabemos o que é uma
rotação, até porque usamos esse termo no dia-a-dia,
quando nos referimos por exemplo:
• uma roda dentada de uma máquina;
• aos ponteiros de um relógio;
• à roda de um veículo;
• à hélice de um avião;
• ao movimento de rotação que a Terra
torno de si mesmo;
faz em
Associado ao conceito de rotação está o conceito de
ângulo orientado.
Deste modo, convencionou-se que o sentido contrário
ao do movimento dos ponteiros de um relógio é o
sentido positivo, enquanto que o sentido do movimento
dos ponteiros de um relógio é o sentido negativo.
Sentido positivo
Sentido negativo
ângulo orientado +90º
ângulo orientado -90º
A figura [A’B’C’D’E’] resulta
da rotação de centro O e
amplitude
90º
da
figura
a
figura
[ABCDE].
Por
seu
lado,
[ABCDE] resulta da rotação
de centro O e amplitude -90º
da figura [A’B’C’D’E’]
O que é uma Rotação?
Uma Rotação de centro O e amplitude  R(O,) é a aplicação que ao ponto O faz
corresponder o próprio O e a cada ponto A da
figura original faz corresponder um ponto A’,
tal que OA  OA' e AOˆ A'  
No exemplo ao lado a
amplitude do ângulo é 60º