1. Determine x no caso a seguir: 2. No triângulo ABC a seguir

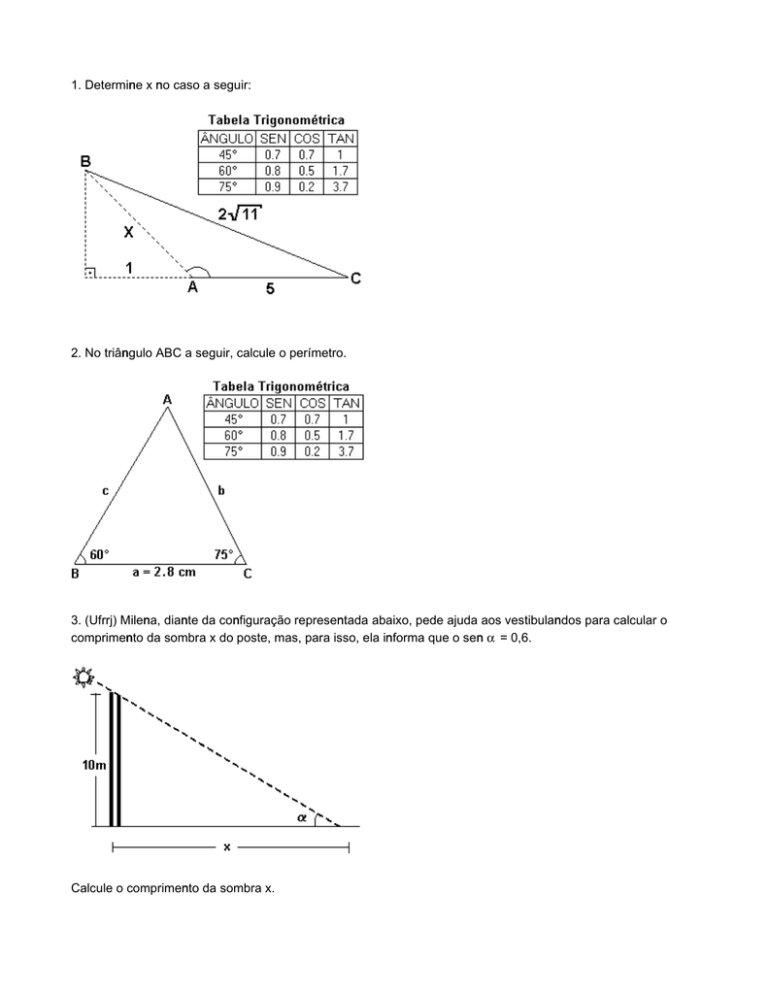
1. Determine x no caso a seguir:
2. No triângulo ABC a seguir, calcule o perímetro.
3. (Ufrrj) Milena, diante da configuração representada abaixo, pede ajuda aos vestibulandos para calcular o
comprimento da sombra x do poste, mas, para isso, ela informa que o sen ‘ = 0,6.
Calcule o comprimento da sombra x.
4. (Unicamp) Caminhando em linha reta ao longo de uma praia, um banhista vai de um ponto A a um ponto B,
cobrindo a distância AB = 1.200 metros. Quando em A ele avista um navio parado em N de tal maneira que o
ângulo NAB é de 60°; e quando em B, verifica que o ângulo NBA é de 45°.
a) Faça uma figura ilustrativa da situação descrita.
b) Calcule a distância a que se encontra o navio da praia.
5. (Unesp) Um farol localizado a 36 m acima do nível do mar é avistado por um barco a uma distância x da base do
farol, a partir de um ângulo ‘, conforme a figura:
a) Admitindo-se que sen(‘) = 3/5, calcule a distância x.
b) Assumindo-se que o barco se aproximou do farol e que uma nova observação foi realizada, na qual o ângulo ‘
passou exatamente para 2‘, calcule a nova distância x' a que o barco se encontrará da base do farol.
6. (Uerj) Considere o triângulo ABC a seguir, onde os ângulos A, B e C estão em progressão aritmética crescente.
Determine os valores de cada um desses ângulos, respectivamente, nas seguintes condições:
a) sen A + sen B + sen C = (3 + Ë3)/2
b) åæ = 2 æè.
7. (Ufpe) Uma ponte deve ser construída sobre um rio, unindo os pontos A e B, como ilustrado na figura abaixo.
Para calcular o comprimento AB, escolhe-se um ponto C, na mesma margem em que B está, e medem-se os
ângulos CBA = 57° e ACB = 59°. Sabendo que BC mede 30m, indique, em metros, a distância AB. (Dado: use as
aproximações sen(59°) ¸ 0,87 e sen(64°) ¸ 0,90)
8. (Unesp) Cinco cidades, A, B, C, D e E, são interligadas por rodovias, conforme mostra a figura.
A rodovia AC tem 40 km, a rodovia AB tem 50 km, os ângulos x, entre AC e AB, e y, entre AB e BC, são tais que
senx = 3/4 e seny = 3/7. Deseja-se construir uma nova rodovia ligando as cidades D e E que, dada a disposição
destas cidades, será paralela a BC.
a) Use a lei dos senos para determinar quantos quilômetros tem a rodovia BC.
b) Sabendo que AD tem 30 km, determine quantos quilômetros terá a rodovia DE.
9. (Unicamp) Sejam A, B, C e N quatro pontos em um mesmo plano, conforme mostra a figura a seguir.
a) Calcule o raio da circunferência que passa pelos pontos A, B e N.
b) Calcule o comprimento do segmento NB.
10. (Ufes) No triângulo ABC da figura, temos AD = CF = BE = 2 cm e DC = FB = EA = (1 + Ë3) cm. Calcule a
medida, em graus, do ângulo AÊD e a área do triângulo DEF.
11. (Ufrj) O objetivo desta questão é que você demonstre a lei dos cossenos. Mais especificamente, considerando
o triângulo da figura a seguir, mostre que
a£ = b£ + c£ - 2bc cosš
12. (Unicamp) Os lados de um triângulo têm, como medidas, números inteiros ímpares consecutivos cuja soma é
15.
a) Quais são esses números?
b) Calcule a medida do maior ângulo desse triângulo.
c) Sendo ‘ e ’ os outros dois ângulos do referido triângulo, com ’ > ‘, mostre que sen£’ - sen£‘ < 1/4.
13. Num triângulo isósceles ABC, cada ângulo da base mede 74° e cada lado congruente 8 cm. Nessas condições
determine: (use a tabela trigonométrica)
a) a medida da altura h.
b) a medida x da base do triângulo.
14. Calcule a diagonal menor do paralelogramo ABCD.
15. (Unesp) Na figura, ABCD é um retângulo, BD = 6 cm, a medida do ângulo ABD é ‘ = 30°, a medida do ângulo
AED é ’ e x = BE. Determine:
a) a área do triângulo BDE, em função de x.
b) o valor de x, quando ’ = 75°.
16. (Ufpe) Considere os triângulos retângulos PQR e PQS da figura a seguir.
Se RS = 100, quanto vale PQ?
a) 100Ë3
b) 50Ë3
c) 50
d) (50Ë3)/3
e) 25Ë3
17. (Unesp) A figura adiante representa o perfil de uma escada cujos degraus têm todos a mesma extensão, além
de mesma altura. Se åæ = 2 m e BðA mede 30°, então a medida da extensão de cada degrau é:
a) (2Ë3)/3 m
b) (Ë2)/3 m
c) (Ë3)/6 m
d) (Ë3)/2 m
e) (Ë3)/3 m
18. (Unesp) Do quadrilátero ABCD da figura a seguir, sabe-se que: os ângulos internos de vértices A e C são
retos; os ângulos CDB e ADB medem, respectivamente, 45° e 30°; o lado CD mede 2 dm.
Então, os lados AD e AB medem, respectivamente, em dm:
a) Ë6 e Ë3.
b) Ë5 e Ë3.
c) Ë6 e Ë2.
d) Ë6 e Ë5.
e) Ë3 e Ë5.
19. (Fuvest) Uma folha de papel ABCD de formato retangular é dobrada em torno do segmento EF, de maneira
que o ponto A ocupe a posição G, como mostra a figura.
Se AE = 3 e BG = 1, então a medida do segmento AF é igual a
a) (3Ë5)/2
b) (7Ë5)/8
c) (3Ë5)/4
d) (3Ë5)/5
e) (Ë5)/3
20. (Mackenzie) Supondo Ë3 = 1,7, a área do triângulo da figura vale:
a) 1,15
b) 1,25
c) 1,30
d) 1,35
e) 1,45
21. (Ufsm) Na instalação das lâmpadas de uma praça de alimentação, a equipe necessitou calcular corretamente
a distância entre duas delas, colocadas nos vértices B e C do triângulo, segundo a figura. Assim, a distância "d" é
a) 50Ë2 m
b) 50 (Ë6)/3 m
c) 50Ë3 m
d) 25Ë6 m
e) 50 Ë6 m
22. (Fuvest) No quadrilátero a seguir, BC = CD = 3 cm, AB = 2 cm, ADC = 60° e ABC = 90°.
A medida, em cm, do perímetro do quadrilátero é:
a) 11.
b) 12.
c) 13.
d) 14.
e) 15.
23. (Mackenzie) A área do triângulo a seguir é:
a) 12 Ë3
b) 18 Ë3
c) 10 Ë3
d) 20 Ë3
e) 15 Ë3
24. (Uerj) Um holofote está situado no ponto A, a 30 metros de altura, no alto de uma torre perpendicular ao plano
do chão. Ele ilumina, em movimento de vaivém, uma parte desse chão, do ponto C ao ponto D, alinhados à base
B, conforme demonstra a figura a seguir:
Se o ponto B dista 20 metros de C e 150 metros de D, a medida do ângulo CÂD corresponde a:
a) 60°
b) 45°
c) 30°
d) 15°
25. (Unirio)
Deseja-se medir a distância entre duas cidades B e C sobre um mapa, sem escala. Sabe-se que AB = 80 km e AC
= 120 km, onde A é uma cidade conhecida, como mostra a figura anterior. Logo, a distância entre B e C, em km,
é:
a) menor que 90.
b) maior que 90 e menor que 100.
c) maior que 100 e menor que 110.
d) maior que 110 e menor que 120.
e) maior que 120.
GABARITO
1. x = 3
2. Perímetro = 7
3. x ¸ 13,33 metros
4. Observe a figura a seguir:
b) d = 600 (3 - Ë3)m
5. a) x = 48m
b) x' = 10,5m.
6. a) A = 30°, B = 60° e C = 90°
b) A = 30°, B = 60° e C = 90°
7. 29 metros.
8. a) BC = 70 km
b) DE = 42 km
9. a) 1 km
b) Ë2 km
10. AÊD = 45°, área = 3Ë(3)/2 cm£
11. Seja h a altura relativa ao lado c e sejam x e y as projeções de a e b sobre c, respectivamente. Então: y = b
cosš e x=c-bcosš.
Pelo Teorema de Pitágoras:
b£ = b£ cos£ š + h£
a£ = (c - bcosš)£ + h£ = c£-2bccosš+b£cos£š+h£
Logo: a£ = b£ + c£ - 2bc cosš.
12. a) 3, 5, 7
b) 120°
c) No Triângulo
Pela lei dos senos, tem-se:
(sen ’)/5 = (sen ‘)/3 = (sen 120°)/7
(sen£ ’ - sen£ ‘)/(25 - 9) = 3/196
sen£ ’ - sen£ ‘ < 1/4
13. a) h = 7,69 cm
b) x = 4,42 cm
14. A diagonal menor do paralelogramo vale 5Ë3.
15. a) 3x/2 cm£
b) 6[(Ë3) -1] cm
16. [B]
17. [E]
18. [C]
19. [D]
20. [D]
21. [A]
22. [B]
23. [C]
24. [B]
25. [C]