Distribuição Normal - ICEB-UFOP

Universidade Federal de Ouro Preto
Instituto de Ciências Exatas e Biológicas – Departamento de Matemática
MTM 510 – Estatística – Turma 22
Professor: Rodrigo Luiz Pereira Lara
Distribuição Normal
A mais importante das distribuições de probabilidade contínuas em todo o
campo da estatística é a distribuição normal. Seu gráfico descreve muitos dos
fenômenos que ocorrem na natureza, na indústria e nas pesquisas.
Dizemos que uma variável aleatória X segue distribuição normal com média  e
variância  2 através da seguinte notação: X ~ N (  ,  2 ) .
Sua função densidade de probabilidade é dada por:
1  x 

 
 
1
f ( x) 
e 2
 2
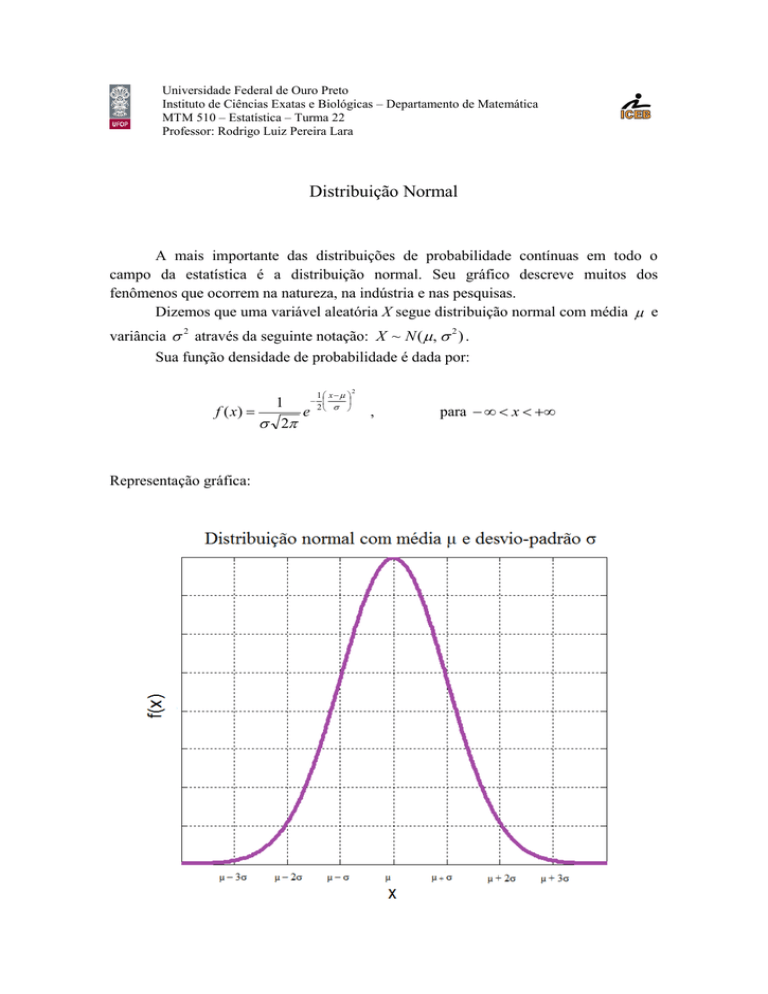
Representação gráfica:
2
,
para    x  
As principais características dessa função são:
a) O ponto máximo de f (x) é o ponto X   .
b) Os pontos de inflexão da função são X     e X     .
c) A curva é simétrica em relação a  .
d) E (X )   e VAR ( X )   2 .
Cálculo de Probabilidades para variáveis aleatórias contínuas
No cálculo de probabilidades de variáveis aleatórias contínuas, devemos calcular
a área abaixo da função densidade de probabilidade no intervalo de interesse, conforme
ilustra a figura seguinte:
Entretanto, a probabilidade representada acima só pode ser resolvida de modo
aproximado e por métodos numéricos. Por essa razão, as probabilidades para o modelo
Normal são calculadas com o auxílio de tabelas:
Para toda v.a. X ~ N(  ,  2 ) utiliza-se uma transformação que conduz sempre ao
cálculo de probabilidades de uma v.a. Z ~ N(0,1).
Considere X ~ N(  ,  2 ) e defina uma nova variável:
Z
X 

Pode-se verificar que essa transformação não afeta a normalidade e, assim, a
variável aleatória Z terá distribuição N(0,1) e será denominada de normal padrão.
Para determinarmos a probabilidade de x [a, b] , procedemos da seguinte
forma:
P a  X  b 
P a    X    b   
X 
b
a
P




 
 
b
a
 P
 Z 

 
 

Os valores para P (0  Z  z) , z  0 , estão apresentados na tabela fornecida em
aula (Magalhães e Lima, 2010, p. 371). Pela simetria da função densidade de
probabilidade da distribuição Normal podemos calcular valores de probabilidades em
outros intervalos, além daqueles informados na tabela.
Exemplo:
O peso de bebês recém-nascidos pode ser modelado pela distribuição normal com média
3 kg e desvio-padrão 0,48 kg. Seja a variável aleatória X ~ N (3; 0,482 ) . Calcule a
probabilidade de um bebê selecionado aleatoriamente pesar:
a) Entre 3 e 3,4 kg.
b) Mais que 3,2 kg.
c) Menos de 2 kg.
a) Solução:
Note que a probabilidade que queremos obter é dada pela área do gráfico a seguir:
Que é a mesma probabilidade obtida pela distribuição Normal Padrão:
X 
3,4   
3 
P 3  X  3,4  P 




 
 
X 
3,4  3 
 33
P




0,48 
 0,48
 P 0  Z  0,83
 0,2967

Tabela da distribuição normal padronizada (ver Magalhães e Lima [2010, p. 271])
Primeira casa decimal
de z
0
0,0
0,1
0,2

0,8

3,7
3,8
3,9
b) Resp.: 0,3372.
Segunda casa decimal de z
2
3
4
5
1
↓
↓
→
→
→
→
0,2967
c) Resp.: 0,0188.
...
9