Jogos com números – Números ocultos - 2ª Parte

INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
Jogos com números – Números ocultos - 2ª Parte
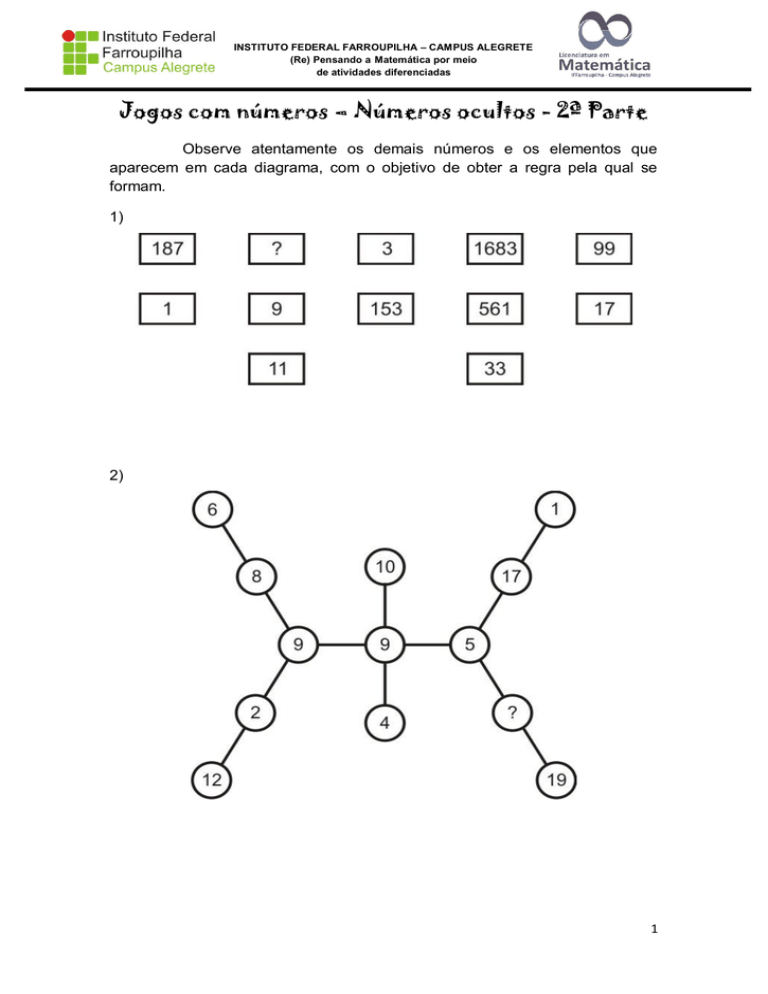
Observe atentamente os demais números e os elementos que
aparecem em cada diagrama, com o objetivo de obter a regra pela qual se
formam.
1)
2)
1
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
3)
4)
5)
6)
2
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
7)
8)
3
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
9)
10)
4
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
11)
12)
13)
5
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
Gabarito – 2ª Parte
1) Na figura aparecem todos os
divisores de 1.683, aleatoriamente,
exceto 51, que é o número que deve
substituir o ponto de interrogação.
2) A soma dos três números alinhados é 23,
portanto, o número que falta é –1.
3) Os números situados nos círculos aos
quais apontam as setas são calculados a
partir da decomposição em fatores primos
dos números situados nos lugares de onde
as setas portem, eliminando os fatores
comuns
a
ambos
e
multiplicando
os
restantes. Para que fique mais claro,
mostramos os cálculos de maneira mais detalhada;
– Na primeira coluna, do 4 e do 6 resulta de novo o 6. 4=2x2 e 6=2x3.
Portanto, o 4 e o 6 têm o 2 como fator comum. Se eliminarmos esse fator,
permanecem um 2 e um 3, cujo produto é igual a 6, que é o resultado.
– Na segunda coluna, do 15 e do 6 obtém-se o 10. 6. 15=3x5 e 6=2x3. Se
prescindimos do 3, que é o fator em comum, sobram-nos o 5 e o 2, que
multiplicados resulta 10.
– Na terceira coluna, o 12 e o 8 produzem o 6. 12=2x2x3 e 8=2x2x2. Afastando
os fatores comuns (o 2 que aparece duas vezes, nos restam o 3 e o 2, cujo
produto de sua multiplicação é 6.
6
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
– Na quarta coluna, do 14 e do 3 obtém-se o 42. 14=2x7 e 3=3. Visto que não
há fatores comuns, não há o que se eliminar, assim, realiza-se o produto de 2,
7 e 3, cujo resultado é 42.
Executando o mesmo procedimento na quinta coluna, pode-se concluir que o
número que falta é o 28,.
4) Quando três números aparecem conectados
em linha reta, o que ocupa a posição central é
igual à média aritmética dos outros dois. De
fato, 12 é a média aritmética de 20 e 4, como
também o é a de 16 e 8. Por outro lado, a média
aritmética de 16 e 6 é 11. Portanto, para que se
prossiga
verificando
essa
propriedade,
o
número que falta deve ser o 18.
5) O número 60 possui
12
divisores
positivos
(1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60), o número 12 tem 6 divisores positivos
(1, 2, 3, 4, 6, 12), o 6 te 4 (1, 2, 3, 6), o 4 tem 3 (1, 2, 4) e o três tem 2 (1, 3).
Dessa forma, na sequência dada, cada número indica a quantidade de
divisores positivos que tem o número que o antecede. Assim, o número que
falta é o 2.
6) Ao dividir-se 619 por 3
e
desconsiderar-se
o
resto, o resultado é 206; se esse número também for dividido por 3, levando-se
em conta unicamente o quociente e não o resto, obtém-se 68; e assim
sucessivamente. Consequentemente, na sequência dada, cada número é
determinado a partir da parte inteira do resultado da divisão do elemento
anterior por 3.
7
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
7) O número a que se dirige cada seta é
calculado somando-se seis unidades ao mínimo
múltiplo comum dos números situados na base
da seta em questão.
8)
Quaisquer
três
números
alinhados
constituem uma “terna pitagórica”, ou seja, o
quadrado do maior deles é igual à soma dos
quadrado dos outros dois.
9) Seguindo a sequência indicada pelas
setas, cada número é obtido a partir do
anterior, realizando certa operação entre
esse e a “posição” que ocupa, ou seja,
com o número da fileira e da coluna em
que se encontra. A operação que deve ser
realizada é determinada pelas setas,
conforme a direção que apontam, para cima, para baixo, para a esquerda ou
para a direita. Em suma, quando a seta aponta para a esquerda, deve-se
somar o número em questão, o da fileira e o da coluna; quando a seta aponta
para a direita, subtrai-se o número da fileira e da coluna do número
considerado; quando a seta aponta para baixo, calcula-se a diferença (em valor
absoluto) entre a fileira e a coluna e se subtrai essa quantidade do número
considerado; finalmente, quando a seta aponta para cima, soma-se a diferença
(também em valor absoluto) entre a fileira e a coluna do número considerado.
Para compreender melhor, vamos observar os primeiros números:
8
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
O primeiro (do qual parte uma seta e ao qual não chega nenhuma) é o 20, que
ocupa a fileira 1 e coluna 3. Para passar ao seguinte, há uma seta que aponta
para a esquerda, que indica que você deve somar os três números (20, 1 3 4),
resultando 24.
O 24 está na fileira 1 e coluna 2. A seta para a esquerda indica novamente que
você deve somar esses três números , resultando 27.
O 27 está na fileira 1 e coluna 1. Realizando a diferença entre o número da
fileira e da coluna, resulta 1–1=0. Portanto, como a seta aponta para baixo,
temos que subtrair 0 de 27, obtendo-se mais uma vez 27.
O 27 está na fileira 2 e na coluna 1. Neste caso, como a seta aponta para a
direita, deve-se subtrair 2 e 1 de 27, obtendo-se 24.
E assim fazemos sucessivamente para os outros valores.
10) Cada quadrado representa uma matriz 2x2,
das três que aparecem na fileira superior, o
produto das duas primeiras é igual a terceira. O
mesmo ocorre na segunda fileira, na qual,
certamente,
aparece
a
chamada
“matriz
identidade”.
11) As somar-se os números que estão
conectados horizontalmente na primeira
linha, obtém-se 27; se somam-se os da
segunda, resulta 24; na terceiras, 21; na
quarta, 18; é fácil observar que a soma do
números de uma fileira é inferior em três
unidades à soma da fileira anterior.
Portanto a soma dos números da quinta
fileira deve ser 15. Ora, nesta linha estão os números 1, 1, 5, 1 e 9, cuja adição
é igual a 17, logo, o número que falta deve ser –2.
9
INSTITUTO FEDERAL FARROUPILHA – CAMPUS ALEGRETE
(Re) Pensando a Matemática por meio
de atividades diferenciadas
12) Obtém-se cada número somando os dois situados abaixo dele e dividindo
por 3 o resultado de tal adição.
13) Pode-se observar que o produto de três números alinhados é igual a 720.
Assim, o número que falta é 16.
10