Capítulo 2 Energia em Processos Térmicos: o Primeiro Princípio da
Termodinâmica
Tópicos do Capítulo
2.1
2.2
2.3
2.4
2.5
2.6
2.7
Calor e Energia Interna
Calor Específico e Calorimetria
Calor Latente
Trabalho e Calor em Processos Termodinâmicos
Primeiro Princípio da Termodinâmica
Algumas Aplicações do Primeiro Princípio da Termodinâmica
Mecanismos de Transferência de Energia
Físico inglês, Joule recebeu alguma educação formal
em matemática, filosofia e química, mas
predominantemente foi autodidacta. Sua pesquisa o
levou ao estabelecimento do princípio de
conservação de energia. O estudo que fez da relação
quantitativa entre dois efeitos eléctricos, mecânicos e
químicos do calor culminou no seu anúncio em 1843
da quantidade de trabalho necessária para produzir
uma unidade de energia interna, chamado equivalente
mecânico do calor.
Até aproximadamente 1850, os campos da termodinâmica e da mecânica eram
considerados dois ramos distintos da Ciência, e a lei da conservação de energia parecia
descrever somente determinados tipos de sistemas mecânicos. Entretanto, experimentos
realizados em meados do século XIX pelo físico inglês James Joule (1818-1889) e
outros cientistas, demonstraram que a energia pode entrar num sistema (ou abandonálo), através do calor e do trabalho. Hoje a energia interna é tratada como uma forma de
energia que pode ser transformada em energia mecânica e vice-versa. Uma vez que o
conceito de energia se tornou mais abrangente para incluir a energia interna, a lei da
conservação de energia emergiu como uma lei universal da natureza.
Este capítulo focaliza o desenvolvimento do conceito de calor, estendendo nosso
conceito de trabalho aos processos térmicos, apresentando o Primeiro Princípio da
Termodinâmica (ou Primeira Lei da Termodinâmica) e investigando algumas aplicações
importantes.
Nota. Energia interna = Energia térmica +Energia de ligação.
16
Figura 2.1 Dispositivo de Joule para medir o equivalente mecânico do calor. O trabalho
realizado sobre a água pelos pesos em queda (em joules), rodam as pás produzindo um
aumento de temperatura, equivalente à absorção, pela água, de uma determinada
quantidade de calor (em calorias). Desta equivalência determina-se a relação da caloria
e joule.
2.1 Calor e Energia Interna
É muito importante fazer a distinção entre energia interna e calor, porque esses termos
tendem a ser usados com o mesmo significado na comunicação diária. Você deve ler as
seguintes descrições com cuidado e tentar usar correctamente esses termos porque eles
não são permutáveis – têm significados muito diferentes.
Agora vamos definir formalmente a energia interna:
A energia interna, U (ou Eint) é a energia associada aos componentes
microscópicos de um sistema – átomos e moléculas – quando vistos a partir de um
referencial em repouso em relação ao centro de massa do sistema.
A última parte da definição indica que a U não inclui a energia cinética do
sistema através do espaço. A energia interna inclui a energia cinética associada ao
movimento aleatório translacional, rotacional e vibratório das moléculas que compõem
o sistema, a energia potencial intramolecular (no interior das moléculas) bem como a
energia potencial intermolecular (entre as moléculas – “energia de ligação”). O modelo
de gás ideal fundamenta-se em moléculas, que são consideradas partículas pontuais.
Para estas partículas a U está associada somente a energia cinética traslacional total dos
átomos. Para gases diatómicos e poliatómicos mais complexos, a energia interna inclui
outras formas de energia molecular, tais como a energia cinética rotacional e a energia
cinética e potencial associada com as vibrações moleculares.
É útil associar a energia interna à temperatura de um objecto, mas essa relação é
limitada, porque como veremos mais adiante, a variação da energia interna também
pode ocorrer na ausência da variação da temperatura. Isto acontece na mudança de fase.
Neste caso a U está associada à energia de ligação (energia potencial intermolecular)
entre as moléculas num líquido ou num sólido.
17
O calor já foi introduzido anteriormente na mecânica, como um possível método
de transferência de energia, mas agora vamos apresentar uma definição formal do Calor:
Calor é um mecanismo pelo qual a energia é transferida entre um sistema e
seu ambiente por causa da diferença de temperatura entre eles. É também uma
quantidade de energia Q transferida por esse mecanismo.
Supomos um recipiente com água em contacto com uma chama de gás. A
energia entra na água pelo calor dos gases quentes na chama e a energia interna da água
aumenta como resultado. É incorrecto dizer que a água tem mais calor à medida que o
tempo passa.
Como esclarecimento adicional do uso da palavra calor, considere a
distinção entre trabalho e energia. O trabalho feito sobre (ou por) um sistema é uma
medida da quantidade de energia transferida entre sistemas e seu ambiente, enquanto a
energia mecânica do sistema (cinética ou potencial) é uma consequência de seu
movimento de coordenadas. Assim, quando uma pessoa realiza trabalho sobre um
sistema, a energia é transferida da pessoa para o sistema. Não faz sentido algum falar
sobre o trabalho num sistema (um sistema não “tem” trabalho) – podemos fazer
referência somente ao trabalho feito sobre ou por um sistema quando algum processo
ocorreu em que a energia foi transferida para o sistema, ou saiu do sistema. Do mesmo
modo não faz sentido algum usar o termo calor (um sistema não “tem” calor), a menos
que a energia tenha sido transferida em consequência de uma diferença de temperatura.
Unidades de calor
No início do desenvolvimento da termodinâmica, antes dos cientistas reconhecerem que
havia uma conexão entre a termodinâmica e a mecânica, o calor era definido em termos
das variações de temperatura que ele produzia num corpo, e utilizava-se uma unidade
separada de energia, a caloria, para o calor. A caloria (cal) era definida como o calor
necessário para elevar a temperatura de 1g de água de 14.5 o C para 15.5 o C .
Em 1948, os cientistas concordaram que, como o calor (assim como o trabalho)
é uma medida da transferência de energia, e sua unidade no SI deveria ser o joule
(Figura 2.1). A caloria é definida agora como sendo exactamente 4.186 J:
1 cal 4.186 J
(2.1)
esta equação também é conhecida como o equivalente mecânico de calor.
É importante observar que a caloria é uma unidade geral de energia de maneira
que poderíamos tê-la empregado para a energia cinética de um corpo, por exemplo. Foi
por razões históricas que ela foi introduzida aqui, mas faremos pouco uso dela como
uma unidade de energia.
Nota. A “Caloria” com C grande, usada para descrever o índice de energia dos alimentos,
corresponde realmente a uma quilocaloria.
2.2 Calor Específico e Calorimetria
A definição de caloria indica a quantidade de energia necessária para elevar a
temperatura de 1 g de uma substância específica – a água – 1 grau, que é 4.186 J. Assim
para elevar a temperatura de 1 kg de água, precisaremos transferir 4186 J de energia.
A quantidade de energia necessária para elevar em 1 grau a temperatura de 1 kg
de uma sustância qualquer, varia de acordo com a substância. Cada substância requer
18
uma quantidade única de energia por unidade de massa para mudar em 1 C a
temperatura dessa substância.
Suponha que uma quantidade de energia Q é transferida para uma massa m de
uma substância, variando desse modo sua temperatura T . O calor específico c da
substância é definido como
c
Q
mT
(2.2)
As unidades do calor específico são J/kg·C. A Tabela 2.1 apresenta os calores
específicos de diversas substâncias. A partir da definição de caloria, o calor específico
da água é 4186 J/kgC.
Tomando como base esta definição, podemos expressar a energia Q transferida
entre um sistema de massa m e o meio em termos da variação de temperatura resultante
T como
Q mcT
(2.3)
Por exemplo, a energia necessária para elevar 3.00 C a temperatura de 0.500 kg de
água é Q=(0.500 kg) (4186 J/kgC) (3.00 C)= 6.28 103 J . Observe que quando a
temperatura aumenta, T e Q são considerados positivos, correspondendo à
energia que flui para dentro do sistema. Quando a temperatura diminui, T e Q
são negativos e a energia flui para fora do sistema.
Se tivermos m gramas de uma substância pura, de calor específico c, a
quantidade de calor Q necessária para elevar a sua temperatura de T é
Q mcT CT , onde mc=C chama-se capacidade térmica (ou calorífica) da
amostra considerada em J / C.
O calor específico elevado da água comparado com a maioria das outras
substâncias comuns (Tabela 2.1) é responsável pelas temperaturas moderadas nas
regiões próximas de grandes volumes de água. Quando no inverno a temperatura cai, a
água transfere energia para o ar, e esta para a terra através dos ventos que sopram nesta
direcção. Isto explica porque os estados litorâneos são mais quentes no Inverno (ver
Figura 2.2).
Enigma 2.1. Imagine que você tenha três amostras, feitas, respectivamente de ferro,
vidro e água. Suponha que elas têm a mesma massa m=1.00 kg, e estão na mesma
temperatura T= 10.0 C. (a) Classifique-as segundo as suas temperaturas, depois que
100 J de energia forem adicionadas a cada uma delas. (b) Classifique-as segundo a
quantidade de transferência de energia pelo calor se cada uma delas aumentar a
temperatura em 20.0 C.
Figura 2.2. Num dia quente, o ar acima da
terra quente se aquece mais rapidamente que
o ar sobre a água fria. O ar mais frio empurra
o ar quente (menos denso) mais para cima,
de acordo com o princípio de Arquimedes. À
noite, a terra arrefece mais rapidamente que
a água, e assim as correntes de ar invertem
suas direcções.
19
Calorimetria
Uma técnica para medir o calor específico de um sólido ou de um líquido é elevar a
temperatura da substância para algum valor, colocá-la num recipiente contendo água de
massa e temperatura conhecidas, e medir a temperatura da combinação depois que o
equilíbrio térmico for alcançado. Definiremos o sistema como a substância e a água. Se
o recipiente for supostamente um bom isolante, de modo que a energia não deixe o
sistema pelo calor (e por nenhum meio), então podemos usar o modelo de sistema
isolado (que não interage com o exterior). Os recipientes que têm essa propriedade são
chamados de calorímetros e a análise executada usando tais recipientes é chamada de
calorimetria.
Figura 2.3. Determinação do calor específico de um corpo.
O princípio de conservação de energia para esse sistema isolado requer que
a energia que sai pelo calor da substância mais quente (de calor específico
desconhecido) se iguale à energia que entra na água. Logo, podemos escrever
Qfrio Qquente
(2.4)
Nota. Para medidas mais precisas é necessário levar em conta o recipiente que contém a água.
Para ver como formulamos o problema de calorimetria (que mencionamos
acima), vamos supor que mx seja a massa de uma substância cujo calor específico
desejamos determinar (ver Figura 2.3); cx o se calor específico; Tx, a sua temperatura
inicial. Sejam ma, Ta e ca os valores correspondentes para a água. Se consideramos T a
temperatura equilíbrio final após a água e a substância se combinarem, utilizando a
equação 2.3 obtemos que a energia ganha pela água é ma ca T Ta e a energia perdida
pela substância de calor específico desconhecido é m x c x T Tx . Substituímos esses
valores na equação (2.4), temos
ma ca T Ta mx c x T Tx
cuja solução para cx fornece
cx
ma ca T Ta
mx Tx T
Substituindo os valores conhecidos no lado direito, podemos calcular o calor específico
da substância.
20
É importante observar que a transferência de energia Q não precisa de ser feita
necessariamente pelo calor. Exemplos:
Durante os primeiros segundos após ligar a torradeira, a temperatura se eleva. O
mecanismo de transferência aqui é a transmissão eléctrica de energia através do
fio eléctrico.
A temperatura de uma batata num forno de microondas aumenta devido à
absorção de microondas. Neste caso, o mecanismo de transferência de energia é
a radiação electromagnética – os microondas.
2.3 Calor Latente
Uma substância frequentemente sofre mudança de temperatura quando há uma
transferência de energia para essa substância. Em algumas situações, entretanto, a
transferência de energia não resulta em mudança de temperatura. Isso pode ocorrer
quando as características físicas da substância mudam de forma, o que é normalmente
chamado de mudança de fase. Algumas mudanças de fase comuns são de sólido para
líquido (fusão), líquido para gás (evaporação) e uma mudança na estrutura cristalina de
um sólido. Todas essas mudanças de fase envolvem uma variação na energia interna,
mas nenhuma variação na temperatura. A energia que aparece como aumento da
energia intermolecular potencial quando as ligações são rompidas, em vez de um
aumento no movimento aleatório das moléculas.
Sabemos da mecânica, que para um corpo que está ligado a Terra por uma força
gravítica ser separado da Terra por uma distância infinita, será necessário adicionar uma
certa quantidade de energia ao sistema corpo-Terra. Através do cálculo dessa energia
poderemos saber a velocidade de escape desse corpo. O fornecimento de energia quebra
a ligação entre o corpo e a Terra. Para separar o electrão do protão num átomo de
hidrogénio, também é necessário fornecer energia ao sistema electrão-protão, a energia
de ionização, que quebra a ligação entre o electrão e o protão. Na mudança de fase,
acontece uma situação semelhante. A energia que é adicionada ao sistema formado
pelas moléculas de uma substância modifica ou rompe as ligações entre as moléculas.
A transferência de energia necessária para a mudança de fase de uma dada
substância de massa m de uma substância pura é
Q mL
(2.5)
onde L é chamado de calor latente da substância e depende da natureza da mudança de
fase, bem como da substância. O sinal adequado na equação 2.5 é escolhido de acordo
com a direcção do fluxo de energia. Quando um cubo de gelo derrete, expressamos a
equação 2.5 como Q mL , mas no caso da água líquida congelando-se, expressamos a
equação 2.5 com sinal negativo: Q mL , porque estamos removendo energia da água.
Calor de fusão L f é o termo utilizado quando a mudança de fase ocorre durante
a fusão ou o congelamento, e calor de evaporação Lv é o termo utilizado quando a
mudança de fase ocorre durante a evaporação ou condensação. Os calores latentes de
diferentes substâncias variam consideravelmente, como pode-se ver na Tabela 2.2.
O calor latente de fusão é a energia necessária para romper todas as ligações
intermoleculares num quilograma de uma substância de maneira a converter a fase
sólida em fase líquida. O calor latente de vaporização é a energia que deve ser
adicionada a um quilograma da fase líquida de uma substância para romper todas as
ligações de maneira a formar um gás.
21
Como pode ser observado na Tabela 2.2, o calor latente de evaporação para uma
dada substância é geralmente muito maior do que o calor latente de fusão. Como está
ilustrado na Figura 2.4, na mudança da fase sólida para a fase líquida, as ligações entre
as moléculas são transformadas em ligações mais fracas. Contudo, na mudança da fase
líquida para a fase gasosa, as ligações são rompidas, criando uma situação na qual as
moléculas de gás não têm essencialmente ligação alguma entre si. Então, é necessário
mais energia para evaporar uma dada massa de substância do que derretê-la.
Figura 2.4. Mudanças de fase
Com o nosso conhecimento de calor latente, podemos entender plenamente o
comportamento de uma substância à medida que se adiciona energia a essa substância.
Considere, por exemplo, a adição de energia a um sistema composto por um bloco de
gelo de 1 g à - 30.0 C num recipiente mantido à pressão constante. Suponha que essa
energia resulte na transformação do gelo em vapor (vapor de água) a 120.0 C. A Figura
2.5 indica a medida experimental da temperatura desde que a energia é adicionada ao
sistema.
Figura 2.5. Gráfico da temperatura versus energia fornecida, quando 1 g de gelo
inicialmente a – 30.0 C é convertido em vapor a 120.0 C.
22
Examinemos cada porção da curva separadamente:
Parte A Durante esta porção da curva, a temperatura do gelo muda de – 30.0 C para
0.0 C. O calor específico do gelo é 2090 J/kgC, então podemos calcular a quantidade
de energia adicionada a partir da equação 2.3:
Q mcgeloT = 1.00 103 kg 2090 J/kgo C 30.0o C 62.7 J
A energia transferida aparece no sistema como energia interna associada ao movimento
aleatório das moléculas de gelo, como representado pela temperatura crescente do gelo.
Parte B
Quando o gelo atinge 0.0 C, a mistura gelo-água se mantém nessa
temperatura – mesmo coma adio de energia – até que o gelo derreta totalmente e se
transforme em água a 0.0 C. Segundo a equação 2.5, a energia necessária para derreter
1.00 g de gelo a 0.0 C é
Q mL f = 1.00 103 kg 3.33 105 J/kg =333 J
Parte C Entre 0.0 C, não ocorre nenhuma mudança de fase. A energia adicionada à
água é utilizada para aumentar a sua temperatura, como na parte A. A quantidade de
energia necessária para aumentar a temperatura de 0.0 C para 100.0 C é
Q mcáguaT = 1.00 103 kg 4.19 103 J/kgo C 100.0o C 419 J
Parte D
A 100.0 C, ocorre outra mudança de fase à medida que a água se
transforma em vapor à 100.0 C. Como aconteceu na parte B, a mistura água-vapor
permanece nessa temperatura constante, desta vez à 100.0 C – e a energia vai para o
rompimento das ligações de maneira que as moléculas do gás se distanciam – até que
todo o líquido tenha se convertido em vapor. A energia necessária para converter 1.00 g
de água em vapor a 100.0 C é
Q mLv = 1.00 103 kg 2.26 106 J/kg 2.26 103 J
Parte E Nesta porção da curva, como nas partes A e C, nenhuma mudança de fase
ocorre, então toda a energia adicionada é usada para aumentar a temperatura do vapor.
A energia que tem de ser fornecida para elevar a temperatura do vapor para 120.0 C é
Q mcvaporT = 1.00 103 kg 2.01 103 J/kgo C 20.0o C 40.2 J
A quantidade total de energia que deve ser adicionada para transformar 1 g de gelo a
– 30.0 C em vapor para 120.0 C é a soma dos resultados de todas as cinco partes da
curva , 3.11 103 J . Inversamente arrefecer 1 g de vapor a 120.0 C em gelo a – 30.0 C,
devemos remover 3.11 103 J de energia.
23
2.4 Trabalho e Calor em Processos Termodinâmicos
Na abordagem macroscópica da termodinâmica, descrevemos o estado de um sistema
com grandezas, tais como pressão, volume, temperatura e energia interna. Essas
grandezas pertencem a uma categoria chamada de variáveis de estado. Para qualquer
condição dada do sistema, podemos identificar valores das variáveis de estado. É
importante observar, entretanto, que o estado macroscópico de um sistema pode ser
especificado apenas se o sistema estiver em equilíbrio térmico interno. No caso de um
gás num recipiente, o equilíbrio interno requer que qualquer porção do gás esteja na
mesma pressão e temperatura. Se a temperatura variar de uma parte a outra do gás, por
exemplo, não podemos especificar uma temperatura única para todo o gás para ser
utilizada na lei do gás ideal.
Uma segunda categoria de variáveis em situações envolvendo energia é a das
variáveis de transferência. Essas variáveis só têm valor diferente de zero se ocorrer
um processo no qual a energia é transferida através da fronteira do sistema. Como a
transferência de energia através da fronteira representa uma mudança no sistema, as
variáveis de transferência não estão associadas com um dado estado do sistema, mas
com a mudança de estado do sistema. Nas secções anteriores discutimos calor como
uma variável de transferência. Para um dado conjunto de condições de um sistema, o
calor não tem valor definido. Podemos assinalar um valor para o calor apenas se a
energia atravessar a fronteira pelo calor, resultando numa mudança no sistema. As
variáveis de estado são características de um processo no qual a energia é transferida
entre um sistema e o meio exterior.
Uma importante variável de transferência para sistemas termodinâmicos é o
trabalho. Na mecânica estuda-se o trabalho realizado sobre partículas. Agora vamos
investigar o trabalho realizado sobre um sistema deformável – o gás. Considere um
gás em equilíbrio térmico contido num cilindro com um pistão móvel sem atrito cuja
área de secção é A (Figura 2.6a).
Figura 2.6.Trabalho realizado por um gás num cilindro de pressão P.
Nota. Por razões históricas escolheu-se W para representar o trabalho feito pelo sistema (pelo
gás). Em outras partes do texto W é o trabalho feito sobre o sistema (sobre o gás). A mudança
afecta somente o sinal de W.
24
O gás ocupa um volume V e exerce uma pressão P nas paredes do cilindro e no pistão.
Adoptamos agora um modelo simplificado no qual o gás é expandido quasiestaticamente, isto é, devagar o suficiente para permitir que o sistema se mantenha em
equilíbrio térmico em todos os instantes. À medida que o pistão é empurrado para fora
do cilindro por uma força interna, Fj de uma distância dr dyj (Figura 2.6b), o
trabalho realizado pelo gás é, de acordo com a definição geral de trabalho
dW F dr Fj dyj Fdy PAdy
F
e o pistão está sempre em equilíbrio. Uma vez que Ady é a
A
mudança no volume do gás dV, podemos expressar o trabalho realizado pelo gás como
pois sabemos que P
dW PdV
(2.6)
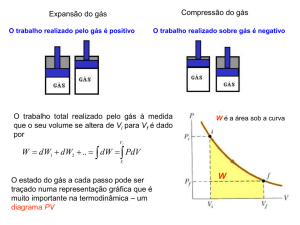
Se o gás é comprimido, dV é negativo (porque o volume diminui) e o trabalho realizado
pelo gás é positivo (ver Figura 2.7a). Se o gás se expande, dV é positivo (porque o
volume aumenta) e o trabalho realizado pelo gás é negativo (ver Figura 2.7b). Se o
volume permanece constante, é nulo o trabalho realizado sobre o gás.
(a)
(b)
Figura 2.7. a) O trabalho realizado pelo gás é positivo; b) O trabalho realizado pelo gás
é negativo.
O trabalho total realizado pelo gás à medida que o seu volume se altera de Vi para Vf é
dado pela integral da equação 2.6:
Vf
W PdV
(2.7)
Vi
Para avaliar esta integral, deve-se saber como varia a pressão com o volume durante o
processo de expansão.
Em geral, a pressão não é constante durante o processo que leva o gás de seu
estado inicial ao seu estado final, mas depende do volume e da temperatura. Se a
pressão e o volume são conhecidos a cada etapa do processo, o estado do gás a cada
passo pode ser traçado numa representação gráfica que é muito importante na
termodinâmica – um diagrama PV:
25
O trabalho realizado pelo gás num processo quasi-estático que leva o gás de
um estado inicial para o estado final é a área debaixo da curva num diagrama PV
calculado entre os estados inicial e final como mostra a Figura 2.8.
Figura 2.8.Um gás é comprimido quasi-estaticamente do estado i para o estado j.
Como sugere a Figura 2.8, para nosso processo de expansão do gás no cilindro, o
trabalho realizado depende da trajectória seguida entre os estados inicial e final. Para
ilustrar este ponto importante, considere várias trajectórias diferentes conectando i e f
(Figura 2.9).
W
W
W
Figura 2.9 O trabalho realizado sobre um gás depende da trajectória.
No processo descrito na Figura 2.9a, inicialmente a pressão do gás diminui de Pi para Pf
por arrefecimento a volume constante Vi, e a partir deste ponto o gás expande-se de Vi
para Vf a uma pressão constante Pf. O trabalho realizado pelo gás nessa trajectória é
Pf V f Vi . Na Figura 2.9b, o volume do gás é reduzido de Vi para Vf a uma pressão
constante Pi. Depois a pressão do gás diminui de Pi para Pf a volume constante Vf e
então o trabalho realizado pelo o gás nessa trajectória é Pi V f Vi , que é maior do que
no processo descrito na Figura 2.9a porque o pistão foi deslocado pela mesma distância
por uma força maior que a da situação da Figura 2.9a. Finalmente para o processo
descrito na Figura 2.9c, em que P e V mudam continuamente, o trabalho realizado sobre
o gás tem um valor intermédio entre os valores obtidos nos dois primeiros processos.
Para calcular o trabalho neste caso, tem de ser conhecida a função P(V), de maneira que
possamos calcular a integral na equação 2.7.
De maneira semelhante, também se descobre que a energia transferida pelo
calor para dentro ou para fora do gás depende do processo. Isso pode ser
demonstrado pelas situações descritas na Figura 2.10. Em cada caso o gás tem o mesmo
volume, temperatura e pressão iniciais e é considerado ideal.
26
Figura 2.10. (a) Um gás à temperatura Ti se expande lentamente absorvendo energia de
um reservatório à mesma temperatura. (b) Um gás expande rapidamente numa região
onde se fez vácuo depois que uma membrana é rompida.
Na Figura 2.10a, o gás é termicamente isolado de sua vizinhança excepto no fundo do
cilindro, onde está em contacto térmico com um reservatório de energia. Um
reservatório de energia é uma fonte de energia interna que é considerada tão grande que
uma transferência finita de energia do reservatório não altera a sua temperatura. O
pistão é mantido na sua posição inicial por um agente externo – sua mão, por exemplo.
Agora a força que segura o pistão é reduzida levemente, de maneira que o pistão sobe
muito lentamente para a sua posição final. Como o pistão sobe, é realizado um trabalho
positivo pelo gás. Durante essa expansão para o volume final Vf apenas a energia
suficiente para manter a temperatura Ti é transferida pelo calor do reservatório para o
gás.
Considere agora o sistema completamente isolado termicamente como apresentado
na Figura 2.10b. Quando a membrana é rompida, o gás se expande rapidamente na
região do vácuo até ocupar o volume final Vf e ficar na pressão Pf. Neste caso, nenhum
trabalho é realizado pelo gás por que nenhuma força é exercida por ele. Além disso,
nenhuma energia é transferida pelo calor através da parede isolante. Como será
demonstrado na alínea 2.6, as temperaturas inicial e final do gás são as mesmas nesse
tipo de expansão.
O estado inicial e final do gás ideal na Figura 2.10a são idênticos ao estado inicial e
final da Figura 2.10b, mas as trajectórias são diferentes. No primeiro caso o gás realiza
trabalho sobre o pistão e a energia é transferida lentamente para o gás. No segundo caso,
nenhuma energia é transferida e o trabalho realizado é nulo. Portanto concluímos que
a transferência de energia pelo calor, assim como o trabalho realizado, depende do
processo seguido entre os estados inicial e final do sistema.
27