"temperatura e pressão"

Capítulo 2
James Joule
2.1
2.2
2.3
2.4
2.5
2.6
2.7
(1818-1889)
Calor e Energia Interna
Calor Específico e Calorimetria
Calor Latente
Trabalho e Calor em Processos Termodinâmicos
Primeiro Princípio da Termodinâmica
Algumas Aplicações do Primeiro Princípio da Termodinâmica
Mecanismos de Transferência de Energia em Processos Térmicos
1
2.1 Calor e Energia Interna
Até ~1850, os campos da termodinâmica e da mecânica eram considerados dois
ramos distintos da Ciência
Experimentos realizados em meados do século XIX pelo físico inglês James Joule
e outros cientistas, demonstraram que a energia pode entrar num sistema (ou
abandoná-lo), através do calor e do trabalho
Hoje a energia interna é tratada como uma forma de energia que pode ser
transformada em energia mecânica e vice-versa
Energia interna e calor
A energia interna, U é a energia associada aos componentes microscópicos de um
sistema – átomos e moléculas
As partículas no modelo de gás ideal são pontuais. Para estas partículas a U está associada
somente a energia cinética traslacional total dos átomos – depende da temperatura
Calor, Q é um mecanismo pelo qual a energia é transferida entre um sistema e
seu ambiente por causa da diferença de temperatura entre eles
Um sistema não tem calor assim como não tem trabalho
2
Unidades de calor
Antes dos cientistas reconhecerem que havia uma ligação entre a termodinâmica e
a mecânica, o calor era definido em termos das variações de temperatura que ele
produzia num corpo, e utilizava-se uma unidade separada de energia, a caloria,
para o calor.
A caloria (cal) era definida como o calor necessário para elevar a temperatura de
1g de água de 14.5 o C para 15.5 o C
Em 1948, os cientistas concordaram que, como o calor (assim como o trabalho)
é uma medida da transferência de energia, e sua unidade no SI deveria ser o
joule
Equivalente mecânico de calor
1 cal  4.186 J
Dispositivo de Joule para determinar a relação da caloria e joule
O trabalho realizado sobre a água pelos pesos em queda (em
joules), rodam as pás produzindo um aumento de temperatura,
equivalente à absorção, pela água, de uma determinada
quantidade de calor (em calorias)
3
2.2 Calor Específico e Calorimetria
O calor específico c de um substância é c 
Q
mT
Q é a energia transferida para a massa m de uma substância, fazendo com que a
sua temperatura varie de T
As unidades do calor específico são J/kg·C
A energia Q transferida do meio para um sistema de massa m varia a sua
temperatura de T
Q  mcT
O calor específico elevado da água comparado com a maioria das outras
substâncias comuns (Tabela) é responsável pelas temperaturas moderadas
nas regiões próximas de grandes volumes de água
4
A Tabela mostra os calores específicos de algumas substâncias a 25 C e pressão
atmosférica
5
O ar mais frio empurra o ar quente (menos denso) mais para cima, de acordo com
o princípio de Arquimedes
6
Calorimetria
Técnica para medir o calor específico de um sólido ou de um líquido
O princípio de conservação de energia para esse sistema isolado requer que a energia que
sai pelo calor da substância mais quente (de calor específico desconhecido) se iguale à
energia que entra na água. Logo, podemos escrever
Qfrio  Qquente
7
Qfrio  Qquente
Água de massa M (ma)
Corpo de massa m (mx)
ma ca T  Ta   mx cx T  Tx 
ca - calor específico da água
Ta - temperatura inicial da água
cx - calor específico do corpo
Tx - temperatura inicial do corpo
T – temperatura de equilíbrio final após a água e a substância se combinarem
Obtemos o calor específico do corpo
ma ca T  Ta 
cx 
mx Tx  T 
Para medidas mais precisas é necessário levar em conta o calorímetro
8
2.3 Calor Latente
Em algumas situações a transferência de energia para uma substância resulta
em mudança de fase
Durante a mudança de fase a temperatura permanece constante
As mudanças de fase comuns são de sólido para líquido (fusão), líquido para gás
(evaporação)
9
A transferência de energia necessária para a mudança de fase de uma dada
substância de massa m de uma substância pura é
Q   mL
L - calor latente da substância
depende da natureza da mudança de
fase e da substância
O calor latente de fusão é a energia necessária para romper todas as ligações
intermoleculares num quilograma de uma substância de maneira a converter a
fase sólida em fase líquida.
fusão ou congelamento
calor de fusão
Lf
O calor latente de vaporização é a energia que deve ser adicionada a um
quilograma da fase líquida de uma substância para romper todas as ligações
de maneira a formar um gás
evaporação ou condensação
calor de evaporação
Lv
10
A Tabela mostra os calores latentes de diferentes substâncias
O calor latente de evaporação para uma dada substância é geralmente muito
maior do que o calor latente de fusão
11
• Na mudança da fase sólida para a fase líquida, as ligações entre as moléculas
são transformadas em ligações mais fracas
• Na mudança da fase líquida para a fase gasosa, as ligações são rompidas,
criando uma situação na qual as moléculas de gás não têm essencialmente
ligação alguma entre si
12
Temperatura versus energia fornecida, quando 1 g de gelo inicialmente a – 30.0 C
é convertido em vapor a 120.0 C.
13
2.4 Trabalho e Calor em Processos Termodinâmicos
Variáveis de estado – pressão, volume, temperatura e energia interna
O estado macroscópico de um sistema pode ser especificado apenas se o sistema estiver
em equilíbrio térmico interno
Variáveis de transferência – trabalho e calor
Essas variáveis só têm valor diferente de zero se
ocorrer um processo no qual a energia é transferida
através da fronteira do sistema
• Trabalho realizado por um sistema deformável
– o gás
O gás ocupa um volume V e exerce uma pressão P
nas paredes do cilindro e no pistão
O gás é expandido quasi-estaticamente, isto é,
devagar o suficiente para permitir que o sistema se
mantenha em equilíbrio térmico em todos os
instantes
 
 
dW  F  dr  Fj  dyj  Fdy  PAdy
porque
F
P
A

dW  PdV
14
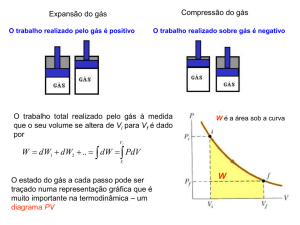
Compressão do gás
Expansão do gás
O trabalho realizado pelo gás é positivo
O trabalho realizado pelo gás é negativo
O trabalho total realizado pelo gás à medida
que o seu volume se altera de Vi para Vf é dado
por
W é a área sob a curva
Vf
W   PdV
Vi
O estado do gás a cada passo pode ser
traçado numa representação gráfica que é
muito importante na termodinâmica – um
diagrama PV
W
15
O trabalho realizado pelo gás depende da trajectória seguida entre os estados inicial
e final
W2
W3
W1
W1  Pf V f  Vi 
W2  Pi V f  Vi 
Vf
W3   PdV
Vi
Para determinar o trabalho W3 é preciso conhecer a função P(V)
W1  W3  W2
16
• Calor em processos termodinâmicos
De maneira semelhante, também se descobre que a energia transferida pelo calor
para dentro ou para fora do gás depende do processo pelo qual é transferido
a) Um gás à temperatura Ti se expande
lentamente absorvendo energia de um
reservatório à mesma temperatura
b) Um gás expande rapidamente numa
região onde se fez vácuo depois que
uma membrana é rompida
Em cada caso o gás tem
o mesmo volume,
temperatura e pressão
iniciais e é considerado
ideal
Portanto concluímos que a transferência de energia pelo calor, assim como o trabalho
realizado, depende do processo seguido entre os estados inicial e final do sistema
17
2.5 Primeiro Princípio da Termodinâmica
Caso especial do princípio da conservação de energia: a única variação na
energia dum sistema é a variação na sua energia interna U, e os únicos
mecanismos de transferência de energia são o calor Q e o trabalho W
Primeiro princípio da termodinâmica
U  Q  W
Q é a energia transferida para o gás
W é o trabalho realizado pelo gás
Significa que a variação da energia interna de um sistema, U é
igual à soma da energia transferida através da fronteira do sistema
pelo calor e a energia transferida pelo trabalho
Quando um sistema é submetido a uma mudança infinitesimal em seu
estado, tal que uma pequena quantidade de energia dQ transferida pelo
calor e uma pequena quantidade de trabalho dW realizado pelo sistema,
a energia interna também varia de uma quantidade pequena dU
U  dQ  dW
18
2.6 Algumas Aplicações do Primeiro Princípio da
Termodinâmica
Processos termodinâmicos: adiabático, isométrico (ou isocórico), isotérmico
e o cíclico
 Processo adiabático
Todas as superfícies do pistão são isolantes perfeitos, de maneira que a
transferência de energia pelo calor não existe
Q=0
Aplicando o primeiro princípio da termodinâmica
U  Q  W  0  W

U  W
O trabalho realizado pelo gás é negativo, representando a
transferência de energia para dentro do sistema, de maneira que a
energia interna aumenta. E quando o gás se expande
adiabaticamente, U é negativo
A expansão livre é um processo adiabático único, em que nenhum trabalho é
realizado sobre o gás. Como Q=0 e W=0 obtemos
.
U  0  U f  U i  0  U f  U i
Não há variação na temperatura
19
durante uma expansão livre adiabática
 Processo isobárico
Processo que ocorre a uma pressão constante
W  PV f  Vi 
Aplicando o primeiro princípio da termodinâmica
U  Q  W
 Processo isométrico (ou isocórico)
No processo isométrico, o volume é
constante e é criado segurando-se o
pistão de maneira que ele não se mova
W=0
Aplicando o primeiro
termodinâmica
U  Q  W  Q  0
princípio

da
U  Q
Toda a energia adicionada ao sistema por meio
do calor, vai para o aumento da energia interna
do sistema
20
 Processo isotérmico
Isoterma
Num processo isotérmico a temperatura é constante
U  0
Aplicando o primeiro princípio da termodinâmica
U  Q  W  0  Q  W  W  Q
A energia que entra no gás por meio do trabalho sai
do gás por meio do calor, de modo que a energia
interna permanece fixa
PV  nRT  P 
Vf
nRT
V
Vf
Vf
nRT
1
Vf
W   PdV  
dV  nRT  dV  nRT ln V V 
i
V
V
Vi
Vi
Vi
nRT ln V f  ln Vi 
ou
 Vf
W  nRT ln 
 Vi



21
 Processo cíclico
O sistema não isolado começa e termina no
mesmo estado
U  0
Aplicando o primeiro princípio da termodinâmica
U  Q  W  0  Q  W
 Q W
A energia adicionada ao sistema na forma de calor, deve ser igual ao trabalho
realizado sobre o sistema durante o ciclo
Os processos cíclicos são muito importantes na descrição das máquinas térmicas
22
2.7
Mecanismos de Transferência de Energia
em Processos Térmicos
 Condução
Em escala atómica há uma troca
de
energia
cinética
entre
moléculas, na qual as moléculas
menos
energéticas
ganham
energia colidindo com moléculas
mais energéticas
- Antes de se inserir a barra na chama, os átomos estão vibrando em torno de suas posições
de equilíbrio
- À medida que a chama fornece energia à barra, os átomos próximos à chama começam
a vibrar com amplitudes cada vez maiores
- Colidem com seus vizinhos e transferem um pouco de sua energia nas colisões
O aumento da vibração das moléculas representa uma elevação de
temperatura do metal
A taxa de condução depende das propriedades da substância
23
Considere um bloco cujo material tem espessura x e uma secção de área A,
cujas faces opostas têm temperaturas T1 e T2, onde T2> T1
Taxa de transferência de energia pelo calor
T2
T2
T1
T1
H  Q / t (Watts)
H é a potência
Q
T
H
 A
t
x
Para um bloco de espessura infinitesimal dx e diferença de temperatura dT,
podemos escrever a lei da condução como
dT
H  kA
dx
k é chamada de condutividade térmica do material
dT / dx
é o gradiente de temperatura (variação da
temperatura com a posição)
24
Suponha que uma substância esteja na forma de uma barra longa e uniforme e de
comprimento L
T2
T1
Está isolada de modo que a energia não
possa escapar pelo calor a partir da sua
superfície excepto nas extremidades, que
estão
em
contacto
térmico
com
reservatórios que têm temperaturas T1 e T2
No estado estacionário a temperatura em cada ponto ao longo da barra é
constante no tempo
dT T2  T1

dx
L

A taxa de transferência de
energia pelo calor será
H  kA
T2  T1
L
k é a condutividade térmica
25
A Tabela mostra a condutividade térmica de diferentes substâncias
26
 Convecção
A energia é transferida pelo movimento de um fluido
Se não fosse pelas correntes de convecção, seria muito difícil ferver a água
À medida que a água é aquecida numa panela, as camadas
inferiores são aquecidas primeiras.
Essas regiões se expandem e sobem porque tem uma densidade
menor que a da água fria. Ao mesmo tempo, a água mais fria e
mais densa vai para o fundo da panela e aí pode ser aquecida.
O mesmo processo ocorre numa
sala aquecida por um aquecedor
27
 Radiação
A energia é transferida pela radiação electromagnética
A origem da radiação electromagnética é a aceleração de cargas eléctricas
Qualquer corpo emite radiação electromagnética devido ao movimento térmico de suas
moléculas
A potência irradiada pelo corpo em Watts
Constante de Stefan-Boltzmann:
H  AeT 4
  5.6696  108
W/m2K4
A é a área da superfície do
corpo em metros quadrados
e
é uma constante chamada
emissividade
T é a temperatura da superfície
do corpo em kelvins
28