30/04/2012
Controle de Obras
Mecânica dos solos
• Diagrama de Mohr
• Critérios de ruptura
Prof. Ilço Ribeiro Jr
1
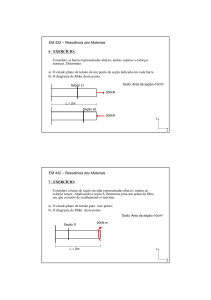
Considerações Preliminares:
Forças em um ponto:
- peso próprio
- forças externas
Várias forças agindo na massa do solo:
Prof. Ilço Ribeiro Jr
2
1
30/04/2012
Tensões no solo
•Em qualquer ponto da massa do solo existem três
planos ortogonais onde as tensões cisalhantes são
nulas. Estes planos são chamados “planos
principais de tensões”. Portanto, as tensões normais
recebem o nome de tensões principais, onde a
maior das tensões atuantes é chamada tensão
principal maior (σ1), a menor é chamada tensão
principal menor (σ3), e a terceira é chamada tensão
principal intermediária (σ2).
Prof. Ilço Ribeiro Jr
3
•Em Mecânica dos Solos, normalmente, despreza-se a
tensão principal intermediária (σ2).
•Supondo k0 < 1, temos:
- σv’0 = γ . z = σ1 (tensão principal maior)
- σh’0 = k0 . σ’v0 = σ3 (tensão principal menor)
Prof. Ilço Ribeiro Jr
4
2
30/04/2012
Estado Plano de tensões
•A maior parte dos problemas de Mecânica dos Solos
permitem soluções considerando um estado de tensões no
plano, isto é, trabalha-se com um estado plano de tensões ou
estado duplo de tensões, que contêm as tensões principais
σ1 e σ3.
•Conhecida a magnitude e direção de σ1 e σ3 é possível
encontrar as tensões normal e cisalhante em qualquer outra
direção, conforme a seguir:
Prof. Ilço Ribeiro Jr
5
Estado Plano de tensões
Prof. Ilço Ribeiro Jr
6
3
30/04/2012
Estado Plano de tensões
Prof. Ilço Ribeiro Jr
7
Estado Plano de tensões
Prof. Ilço Ribeiro Jr
8
4
30/04/2012
Círculo de Mohr
•O estado de tensões em todos os planos passando por um
ponto podem ser representados graficamente em um
sistema de coordenadas em que as abcissas são as tensões
normais (σ) e as ordenadas são as tensões de cisalhamento
(τ).
•O círculo de Mohr tem seu centro no eixo das abcissas.
Desta forma, ele pode ser construído quando se
conhecerem as duas tensões principais, ou as tensões
normais e de cisalhamento em dois planos quaisquer.
Prof. Ilço Ribeiro Jr
9
Círculo de Mohr
•O estado de tensões em todos os planos passando por um
ponto podem ser representados graficamente em um
sistema de coordenadas em que as abcissas são as tensões
normais (σ) e as ordenadas são as tensões de cisalhamento
(τ).
•O círculo de Mohr tem seu centro no eixo das abcissas.
Desta forma, ele pode ser construído quando se
conhecerem as duas tensões principais, ou as tensões
normais e de cisalhamento em dois planos quaisquer.
Prof. Ilço Ribeiro Jr
10
5
30/04/2012
Círculo de Mohr
•Conhecendo-se σ1 e σ3 traça-se o círculo de Mohr. A
inclinação (α) do plano principal maior (PPM),
permite determinar o ponto P (pólo), traçando-se por
σ1 uma reta com esta inclinação.
•Procedimento idêntico pode ser utilizado traçando-se
por σ3 uma paralela ao plano principal menor (ppm).
•Qualquer linha reta traçado através do pólo ou origem
dos planos (ponto P) intersecionará o circulo em um
ponto que representa as tensões sobre um plano
inclinado de mesma direção desta linha.
Prof. Ilço Ribeiro Jr
11
Círculo de Mohr
Prof. Ilço Ribeiro Jr
12
6
30/04/2012
Círculo de Mohr
Prof. Ilço Ribeiro Jr
13
Círculo de Mohr
A resultante de “τ” e “σ” no plano bb é:
e tem uma obliquicidade “θ” igual a tg θ = τ / σ.
Prof. Ilço Ribeiro Jr
14
7
30/04/2012
Tensões Totais, Efetivas e Neutras
O principio básico introduzido por Terzaghi que em solos
saturados a tensão efetiva é igual a
diferença entre a tensão total e a tensão neutra :
σ' = σ - u .
Prof. Ilço Ribeiro Jr
15
Tensões Totais, Efetivas e Neutras
As tensões de cisalhamento em qualquer plano são
independentes da poro-pressão, pois a água não transmite
esforços de cisalhamento.
As tensões de cisalhamento são devidas somente à
diferença entre as tensões normais principais e esta
diferença é a mesma, tanto quanto se consideram as
tensões efetivas como as tensões totais, como se verifica
pela fórmula proposta por Terzaghi.
Os círculos de Mohr para os dois tipos de tensão tem,
portanto, o mesmo diâmetro.
Prof. Ilço Ribeiro Jr
16
8
30/04/2012
Tensões Totais, Efetivas e Neutras
O círculo de tensões efetivas se situa deslocado para a esquerda em
relação ao círculo de tensões totais de um valor igual à tensão neutra
(u). Tal fato é decorrente da tensão neutra atuar hidrostaticamente
(igual em todas as direções), reduzindo as tensões normais totais em
todos os planos de igual valor. No caso de tensões neutras negativas,
o deslocamento do círculo é para a direita.
Prof. Ilço Ribeiro Jr
17
Prof. Ilço Ribeiro Jr
18
9