V- Círculo de Mohr Tensões

Resistência dos Materiais XI
CÍRCULO
CÍRCULO DE
DE
MOHR
MOHR
PARA
PARA
TENSÕES
TENSÕES
Estado Plano de Tensões
Num certo ponto da superfície de um corpo carregado
são conhecidas as tensões em dois planos
perpendiculares
y
σy
σx
τyx
τxy
σx
z
σy
x
Trace um eixo horizontal para marcar as tensões normais σ
τ
Representação Gráfica das
Tensões no Plano de Mohr
σ
Trace um eixo vertical para marcar as tensões tangenciais τ
Marque as tensões normais de
tração à direita da origem
τ
0
Marque as tensões normais de
compressão à esquerda da origem
σ
Marque para CIMA as
tensões tangenciais que giram
o elemento no sentido
HORÁRIO
τ
σ
0
Marque para BAIXO as
tensões tangenciais que giram
o elemento no sentido
ANTI-HORÁRIO
Exemplo
1: σx =σ+ x50MPa;
σy = - 10MPa;
τxy = τyxapresentadas
- 40MPa
Plote
no plano
τ os valores
das tensões
-10
τ
40
y
x
-40
50
50
-40
-10
-10
40
50
σ
Unindo os dois pontos obtém-se a posição do centro do círculo
de Mohr σC = ½ (σ
σx + σy)
τ
40
Observeoo
Observe
triângulo
triângulo
assinalado
assinalado
20
-10
40
C
50
σ
Traceoocírculo
círculo
Trace
comcentro
centroem
em
com
passando
CCeepassando
pelosdois
dois
pelos
pontos
pontos
Os catetos do triângulo valem:
τ
40
40
ττxyxy == 40
20
-10
C
50
½(σ
(σ
½[50-(-10)]
[50-(-10)]==30
30
½
σσxx––σσyy))==½
40
σ
A hipotenusa valerá:
τ
40
[ (σ x − σ y )] + τ xy
1
2
2
40
ττxyxy == 40
2
30 + 40 > 50
2
2
-10
50
½(σ
(σ
½[50-(-10)]
[50-(-10)]==30
30
½
σσxx––σσyy))==½
40
σ
A hipotenusa é o raio R do Círculo de Mohr
τ
σcc--RR
σσmín
mín==σ
-30
==-30
-10
40
40
= RR
50
ττmáx
R===50
50
máx=
20
PORTANTO:
σcc++RR
σσmáx
máx==σ
70
==70
50
σ
As tensões principais ficam assim determinadas:
σσp1p1==σσcc++RR==½½((σσxx ++σσyy))++
[½
[½((
σσp2p2==σσcc––RR==½½((σσxx ++σσyy))--
[½
[½((
ττ
máx
máx
σσxx --σσyy)])] ++((ττxyxy)) ==20+50=70
20+50=70
22
σσxx --σσyy)])] ++((ττxyxy)) ==20-50=-30
20-50=-30
22
σσxx --σσyy)])] ++((ττxyxy)) ==50
50
== [½
[½((
22
22
22
22
40
y 10
Observe ainda na figura formada:
40
τ
40
x
50
Pontoque
que
Ponto
representaoo
representa
estadode
detensão
tensão
estado
noplano
planoque
quetem
tem
no
eixo“x”
“x”como
como
ooeixo
perpendicular
perpendicular
Pontoque
que
Ponto
representaoo
representa
estadode
detensão
tensão
estado
noplano
planoque
quetem
tem
no
eixo“y”
“y”como
como
ooeixo
perpendicular
perpendicular
40
-10
20
50
σ
40
y 10
-10
-20
AA
Ainterseção
direção
direção que
que
dessas
une
une oodireções
pólo
pólo ao
aoéponto
ponto
o chamado
do
do círculo
círculo
PÓLO
correspondente
correspondente àà tensão
tensão σσ21 éé aa direção
direção 21
40
τ
40
x
50
20
σ
50
70
2
40
1
40
y 10
τ
Observe
... é igual
que
à metade
o ângulo
doinscrito,
ângulo central
entre as
direções “1” e assinalado:
“x”, mostrado na figura :
40
40
x
50
θ1
τxy
2θ1
-10
½ (σ
σx – σy)
Sendo: tg 2θ
θ1 = τxy / ½ (σ
σx – σy)
40
σ
50
20
70
1
40
y 10 No caso em estudo: τxy = - 40, σx = 50 e σx = -10
40
τ
40
50
θ1
-10
40
20
x
tg
2θ
θθ2θ
θ=1−=
−29,5º
59,0º
−1,33
29,5
59,0
11=
50
σ
Para o estado de tensão em análise teremos portanto
29,5º
74,5º
29,5
74,5
θθ == −0−0 74,5
29,5º
74,5º
29,5
y
20
-10
70
- 30
-40
50
20
20
50
50
-30
-40
P
τ
40
70
20
-10
50 x
-20
σ
-10
20
40
50
70
Alguns exemplos
de estados de tensão comuns
τ
τ
σ
Tração
Pura
σ
τ
τ
σ
σ
Compressão
Pura
τ
Corte
Puro
Semi
hidrostático
Vaso de
pressão
τ
σ
σ
Tubo sob
pressão e
torção
τ
Flexão
Simples
σ
Tarefa: em cada caso exemplificado
indique a posição ocupada pelo pólo.
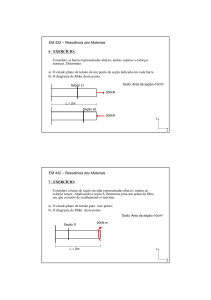
Exercício proposto: para o estado de tensões esquematizado
na figura e utilizando o Círculo de Mohr, pede-se:
y
48 MPa
36 MPa
P
As tensões máximas de tração e
de compressão. Indicar os planos
onde ocorrem;
2)
As tensões máximas de
cisalhamento. Indicar os planos
em que ocorrem;
3)
As componentes normal e
tangencial da tensão ocorrente no
plano “P” assinalado na figura
72 MPa
30º
z
1)
x
fim