Lista de Exercícios 2

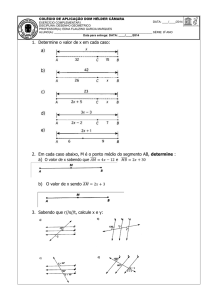
11. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
(a) 35° b) 70°)
a)
b)
LISTA 2 – GEOMETRIA PLANA – PROF. NATHALIE
1º Ensino Médio
01. Qual é o polígono cuja soma dos ângulos internos é igual a 1800°? (dodecágono)
02. Dois dos ângulos externos de um polígono convexo medem 75° e todos os
demais ângulos externos medem 30°. Quantos lados esse polígono possui? (9
lados)
03. (MACK) Num polígono regular, a medida de um ângulo interno é 150°. Determine o
número de lados desse polígono. (12 lados)
04. (MACK) Determine o polígono regular convexo cujo ângulo interno é 7/2 do seu ângulo
externo. (eneágono)
05. Dois ângulos internos de um polígono convexo medem 130° cada um e os demais
ângulos medem 128° cada um. Qual o número de lados desse polígono? (7 lados)
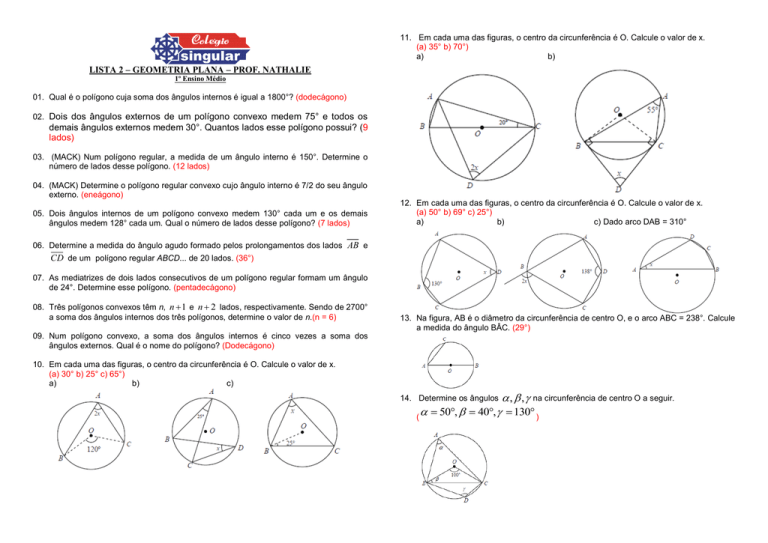
12. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
(a) 50° b) 69° c) 25°)
a)
b)
c) Dado arco DAB = 310°
06. Determine a medida do ângulo agudo formado pelos prolongamentos dos lados AB e
CD de um polígono regular ABCD... de 20 lados. (36°)
07. As mediatrizes de dois lados consecutivos de um polígono regular formam um ângulo
de 24°. Determine esse polígono. (pentadecágono)
08. Três polígonos convexos têm n, n  1 e n  2 lados, respectivamente. Sendo de 2700°
a soma dos ângulos internos dos três polígonos, determine o valor de n.(n = 6)
13. Na figura, AB é o diâmetro da circunferência de centro O, e o arco ABC = 238°. Calcule
a medida do ângulo BÂC. (29°)
09. Num polígono convexo, a soma dos ângulos internos é cinco vezes a soma dos
ângulos externos. Qual é o nome do polígono? (Dodecágono)
10. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
(a) 30° b) 25° c) 65°)
a)
b)
c)
 ,  ,  na circunferência de centro O a seguir.


50

,


40

,

 130 )
(
14. Determine os ângulos
15. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
(a) 75° b) 48°)
a) Dados AMB = 42° e CND = 108°
b) Dados AMB = 132° e AÊB = 90° (x = CND)
19. Na figura, a reta BC passa pelo centro O da circunferência e intercepta a reta DE no
ponto A, BCD = 235° e DÔE = 100°. Calcule a medida do ângulo CÂD. (15º)
16. Se, na figura, as medidas dos menores arcos AB = 20°, BC = 124°, CD = 36° e DE =
90°, então calcule o valor de x. (x = 37°)
20. Em cada uma das figuras, o centro da circunferência é o ponto O. Sendo B e C pontos
de tangência, calcule o valor de x. (a) 60° b) 55°)
a ) Dado BMC = 240°
b)
17. Na figura, temos uma circunferência interceptada pelas retas AC e EC. Com base nos
valores indicados, calcule a medida do ângulo x = CDA. (110º)
21. Em cada uma das figuras, o centro da circunferência é O. Calcule o valor de x.
(a) 5 b) 6)
a)
b)
18. Em cada uma das circunferências de centro O a seguir, calcule o valor de x.
(a) 36° b) 142°)
a) Dados AMB = 106° e CND = 34°
b) Dados AÊB = 42° e CND = 58° (x = AMB)
22. Na figura, a circunferência de centro O está inscrita no triângulo ABC. Sendo P o ponto
de tangência no lado BC, AB = 9 cm, BC = 11 cm e AC = 14 cm, calcule a medida do
segmento BP. (3 cm)
23. Na figura, a circunferência de centro O está inscrita no triângulo retângulo ABC. Sendo
AB = 6 cm, AC = 8 cm e BC = 10 cm, calcule a medida do raio dessa circunferência.
(2 cm)
28. Na figura, sabe-se que CAD = 20° e CED = 70°. Determine o valor de AMB. (30º)
29. Na figura, os pontos A, B e C pertencem à circunferência de centro O. Se
24. Na figura, o quadrilátero ABCD está circunscrito à circunferência de centro O. Sendo
AB = (2x + 1) cm, BC = 10 cm, CD = (3x + 2) cm e AD = 8 cm, calcule a medida do
lado AB. (7 cm)
25. Qual é a medida do ângulo CDA inscrito na circunferência de centro O? (125º)
  150
e
  50 , determine o valor de  . (35º)
30. Num paralelogramo, a medida de um lado é 2/3 da medida do outro. Sabendo que seu
perímetro é 120 cm, calcule o comprimento de cada lado. (24 cm e 36 cm)
31. Num trapézio retângulo o menor ângulo é 5/7 do maior. Determine a medida dos seus
ângulos internos. (75°, 90°, 90° e 105°)
32. Num trapézio retângulo, a medida do maior ângulo interno é o quádruplo da medida do
menos. Determine a medida do menos doa ângulos desse trapézio. (36°)
26. Em um círculo de centro O, está inscrito o ângulo
determine o valor de  . (25º)
.
Se o arco AMB mede 130°,
33. Sabendo que os ângulos obtusos de um losango são expressos por x + 80° e 2x + 20°,
calcule as medidas dos 4 ângulos desse losango. (40°, 40°, 140° e 140°)
34. Num paralelogramo, os ângulos agudos medem a metade dos ângulos obtusos.
Determine as medidas dos ângulos desse paralelogramo. (60°, 60°, 120° e 120°)
35. Num triângulo ABC, AB = 20 cm e AC = 28 cm. Por um ponto D, sobre o lado AB e
distante 5 cm do vértice A, traça-se o segmento DE, paralelo ao lado BC e com o ponto
E sobre o lado AC. Calcule a medida do segmento AE. (7 cm)
27. Na figura abaixo, determine o valor de x. (20º)
36. O proprietário de uma área quer dividi-la em três lotes, conforme a figura abaixo.
Determine os valores de a, b e c, em metros, sabendo-se que as laterais dos terrenos
são paralelas e que a + b + c = 120m. (a = 30 m, b = 36 m e c = 54 m)
37. Um feixe de paralelas determina sobre uma transversal t 1 os segmentos AB e BC, tais
que AB = (x + 1) cm e BC = (x + 8) cm. O mesmo feixe determina sobre uma segunda
transversal t2 os segmentos EF e FG tais que EF = (x + 10) cm e FG = (x + 20) cm; os
pontos A e E estão alinhados. Qual é o valor da soma AB + BC + EF + FG? (119 cm)
38. Duas avenidas se cruzam em um ponto A. Essas avenidas cortam três ruas, r 1, r2 e r3,
que são paralelas entre si. Os segmentos AD, AB e BC representam quarteirões da
Avenida 2, enquanto os segmentos AM, AN e NP representam quarteirões da Avenida
1. Na figura estão indicados os comprimentos, em metros, desses quarteirões.
Determine os comprimentos dos quarteirões representados pelos segmentos BC e AM.
(128 m e 37,5m)
43. Na figura abaixo, determine o valor de x. (R. 11,25)
44. A sombra de um poste vertical, projetada pelo sol sobre o chão plano, mede 12 m.
nesse mesmo instante, a sombra de um bastão vertical de 1 m de altura mede 0,6 m.
Determine a altura do poste. (R. 20 m)
45. Na figura, o triângulo ABC é retângulo em A, ADEF é um quadrado, AB = 1 e AC = 3.
Quanto mede o lado do quadrado? (R. 0,75)
39. Dois lotes estão representados na figura abaixo. Calcular as medidas de frente para a
rua R de cada um dos terrenos, respectivamente. (22 m e 33 m)
46. Na figura ao lado, as retas AB e CD são paralelas. Sabendo-se que AB  136cm ,
CE  75cm e CD  50cm . Calcule a medida do segmento AE . (204 cm)
40. Num eclipse total do Sol, o disco lunar cobre exatamente o disco solar, o que
comprova que o ângulo sob o qual vemos o Sol é o mesmo sob o qual vemos a Lua.
Considerando que o raio da Lua é 1.738 km e que a distância da Lua ao Sol é 400
vezes a da Terra à Lua, calcule o raio do Sol. (R. 696.938 km)
47. Na figura, PQRS é um retângulo tal que o lado PQ é o dobro do lado QR.
Considerando os dados da figura determine o perímetro desse retângulo. (36 cm)
41. Um menino de 1,50 m de altura observa, num dia de sol, a sombra de uma torre de
radio emissora e a sua própria sombra. Não dispondo de fita métrica ou de trena, ele
toma um cordão, mede sua sombra e a compara com a da torre, verificando ser esta
10 vezes maior do que a sua. Calcule a altura da torre. (R. 15 m)
42. Na figura abaixo, tem-se: AE = 1 cm, BC = 3 cm e CD = 7 cm. Determine a medida em
centímetro de BE. (R. 5 cm)
ˆ
ˆ
48. Na figura, se ABC  AED , AD  8cm , DB  2cm e AE  5cm , calcule a medida
do segmento EC . (11 cm)
49. O sol incide sobre uma pessoa de 1,60 m de altura e sua sombra projetada sobre um
piso horizontal é de 2,40 m. Um poste vertical, situado no mesmo lugar, é projetado
sobre o mesmo piso. Algumas horas mais tarde, a sombra da pessoa, no mesmo piso
e lugar é de 2,00 m, enquanto que o a sombra do poste recuou 2,50 m. Calcule a
altura do poste.
(10 m)
54. Na figura, as circunferências têm raios 3 m e 4 m. Calcule a altura h do triângulo. (32
cm)
50. Calcule o valor de x em cada uma das figuras. (a) 8/3 b) 96)
a)
b)
55. Para estimar a profundidade de um poço com 1,10 m de largura, uma pessoa cujos
olhos estão a 1,60 m do chão posiciona-se a 0,50 m de sua borda. Desta forma, a
borda do poço esconde exatamente seu fundo, como mostra a figura. Com os dados
acima, calcule a profundidade do poço. (3,52 m)
51. A figura mostra um quadrado inscrito num triângulo de base 20 cm e altura 12 cm.
Calcule a medida do lado desse quadrado. (15/2 cm)
52. Os triângulos ABC e CDE da figura são retângulos em B e em E
e CD
é
perpendicular a BC . Se AB  12cm , BC  16cm e DE  4cm , calcule a medida de
CE . (3 cm)
56. Um crítico de arte olha, através de uma câmara escura que tem 50 cm de
comprimento, para um quadro pendurado de 3 metros de altura, cuja base está a 1,20
metros acima do solo, conforme a figura a seguir. Sabendo-se que o quadro fornece
uma imagem de 15 cm. Determine a distância "x" da câmara ao quadro, em metros.
(10 m)
53. Determine o valor de x no trapézio ABCD da figura. (12 cm)
57. Há muitas histórias escritas sobre o mais antigo matemático grego que conhecemos
Tales de Mileto. Não sabemos se elas são verdadeiras, porque foram escritas
centenas de anos após sua morte. Uma delas fala do método usado por ele para medir
a distância de um navio no mar, em relação a um ponto na praia. Uma das versões diz
que Tales colocou uma vara na posição horizontal sobre a ponta de um pequeno
penhasco, de forma que sua extremidade coincidisse com a imagem do barco.
Conhecendo sua altura (h), o comprimento da vara (c) e a altura do penhasco (d), ele
calculou a distância x em relação ao barco. Determine a distância do navio à praia com
estes dados: h = 1,80m; c = 0,75m; d = 298,20m. (125 m)
58. Na figura os segmentos com “marcas iguais” são congruentes. Determine os valores
de x e y. (x = 4 e y = 6)
59. Se P é o incentro de um triângulo ABC e BPˆ C  125 , determine  . (70°)
60. Se H é o ortocentro de um triângulo isósceles ABC de base BC e BHˆ C  130 ,
determine os ângulos desse triângulo. (65°, 65° e 50°)
61. Sendo H o ortocentro de um triângulo acutângulo ABC e BHˆ C  150 , determine a
medida do ângulo  . (30°)
62. Em um triângulo ABC, os ângulos A e B medem, respectivamente, 76° e 34°.
Determine o ângulo agudo formado pela mediatriz do lado BC com a bissetriz do
ângulo C. (55°)
63. Em um triângulo ABC, os ângulos B e C medem, respectivamente, 74° e 32°. Se I é o
ˆ O . (21°)
incentro e O é o ortocentro, calcule a medida do ângulo IA
AB e CD . Se DP e CP são bissetrizes,
determine o ângulo ABC. (ABC = 140°)
64. ABCD é trapézio de bases