1 me - Trigonometria no Triangulo Retangulo F

1º MATERIAL EXTRA – 3ª série Ensino Médio – PROF. PASTANA
Trigonometria no Triângulo Retângulo
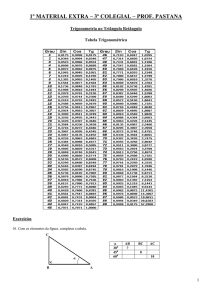
Tabela Trigonométrica
Exercícios
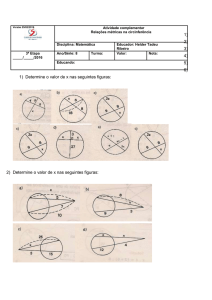
01. Com os elementos da figura, completar a tabela.
C
α
300
450
600
α
B
AB
7
BC
AC
8
10
A
1
02. Uma escada, apoiada em uma parede, num ponto que dista 2,5 m do solo, forma com essa parede um ângulo de 600. Calcular o
comprimento dessa escada.
03. A uma distância de 40 m, uma torre é vista sob um ângulo de 200. Desprezando-se a altura do observador, determinar a altura
da torre.
04. A presença de um pântano infestado de crocodilos torna inacessíveis as margens de um rio.
D
C
180
250
A
B
50 m
Os pontos C e D são vistos a partir dos pontos A e B como mostra a figura. Calcular a largura do rio.
05. Uma pessoa encontra-se a 100 m de uma árvore. Seus olhos estão a 1,75 m do solo, que é horizontal. A árvore é vista sob um
ângulo de 210.
210
1,75 m
100 m
Calcular a altura da árvore.
06. Um navio, navegando em linha reta, passa sucessivamente pelos pontos A e B. O comandante, quando o navio está no ponto
A, observa um farol no ponto C e calcula o ângulo AĈB = 300. Sabendo-se que o ângulo ABC = 900 e que a distância entre os
pontos A e B é de 6 milhas, pergunta-se qual a distância entre o farol e o ponto B.
07. Para obter a altura h de uma chaminé, um engenheiro, com um aparelho especial, estabeleceu a horizontal AB e mediu os
ângulo α e β, tendo a seguir medido BC = k.
D
A
β
α
B
h
k
C
Determinar a altura da chaminé, em função de α, β e k.
2
08. Um avião levanta voo para ir da cidade A à cidade B, situada a 500 km de distância. Depois de voar 250 km em linha reta, o
piloto descobre que a rota está errada e, para corrigi-la, ele altera a direção de voo de um ângulo de 900. Se a rota não tivesse sido
corrigida, a que distância ele estaria de B após ter voado os 500 km previstos?
09. Uma pessoa cujos olhos estão a 1,80 m de altura em relação ao chão avista o topo de um edifício segundo um ângulo de 300
com a horizontal. Percorrendo 80 m no sentido de aproximação do edifício, esse ângulo passa a medir 600. Usando o valor 1,73
para a raiz quadrada de 3, calcular o valor aproximado da altura do edifício.
10. (desafio) Para medir a altura de uma torre vertical DE, toma-se no plano horizontal que passa pela base D, o segmento AB de
comprimento 12 m, cujo ponto médio é C. Medem-se os ângulos DÂE, DBE e DĈE, verificando-se que medem, respectivamente,
450, 450 e 600. Determinar a altura da torre.
Gabarito
01. (BC = 7√3/3; AC = 14√3/3) (AB = 8; AC = 8√2) (AB = 5; BC = 5√3)
05. 38,15 m
06. 6√3 milhas
07. k(tgα + tgβ)/tgα
08. 500 km
02. 5 m
09. 71 m
03. 14,56 m
04. 23,31 m
10. 3√6 m
3