Geotecnia II - Prova II - 23/06/2015 Prof. Flavio A. Crispim 1/4

Geotecnia II - Prova II - 23/06/2015
Prof. Flavio A. Crispim
Universidade do Estado de Mato Grosso - UNEMAT - Campus de Sinop
Curso de Engenharia Civil
Obs.: Ao resolver as questões explique o que está sendo feito. Mostre os cálculos e procedimentos
utilizados para chegar às respostas dos problemas propostos. Adotar γw = 9,81kN/m³.
Questão 1 (2,0).
Quais são as diferenças entre um adensamento oedométrico (ensaio de adensamento
incremental) e um adensamento hidrostático?
O adensamento oedométrico é anisotrópico, ou seja, a relação entre tensão principal maior (1) e tensão
principal menor (3) é diferente de 1. No ensaio aplica-se a tensão 1 e a tensão 3 gerada é função das
propriedades de solo. Por outro lado, o adensamento hidrostático é isotrópico. A tensão é aplicada por
pressão em água e assim as tensões são iguais em todas as direções (princípio de Pascal),
particularmente, 1 igual a 3.
No adensamento oedométrico o caminho de tensões tem inclinação não nula em relação à horizontal. No
ensaio hidrostático o caminho de tensões é horizontal (inclinação 0).
Questão 2 (2,5).
Uma série de três corpos de prova de argila saturada foi submetida a ensaio de
cisalhamento direto. O resultado indicou uma envoltória Mohr-Coulomb com c’ = 0 e tan ’ = 0,58. Com
outra amostra desta argila foi realizado ensaio triaxial não drenado com tensão de adensamento de
100 kPa. A tensão de cisalhamento no plano de ruptura encontrada foi de 46 kPa.
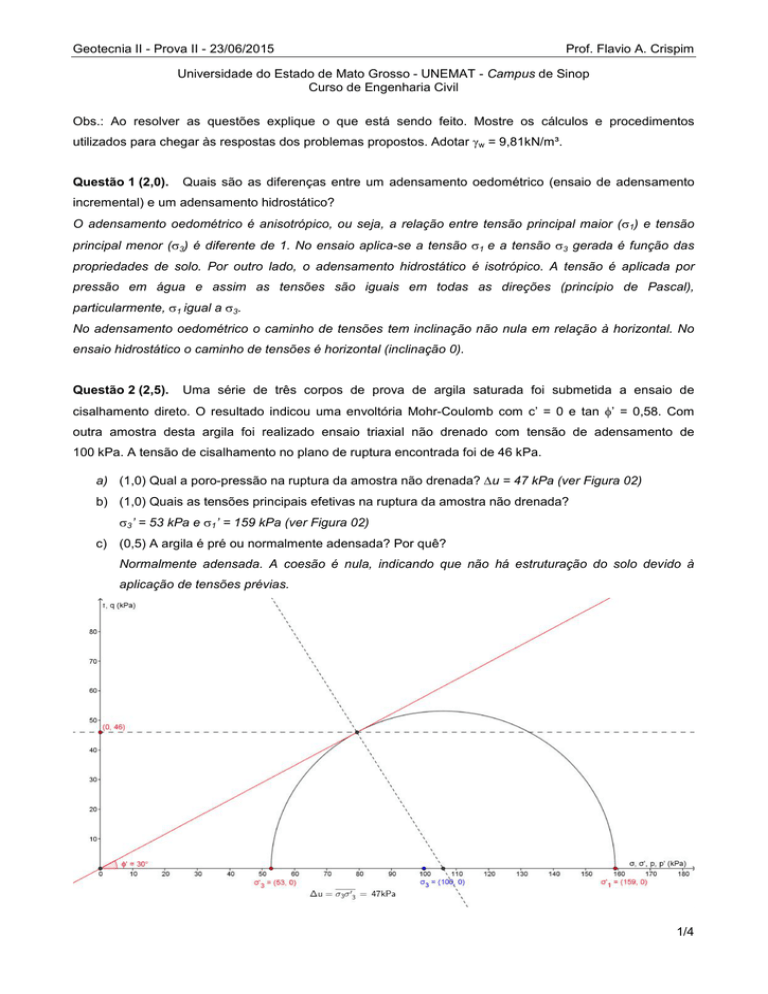
a) (1,0) Qual a poro-pressão na ruptura da amostra não drenada? u = 47 kPa (ver Figura 02)
b) (1,0) Quais as tensões principais efetivas na ruptura da amostra não drenada?
3’ = 53 kPa e 1’ = 159 kPa (ver Figura 02)
c) (0,5) A argila é pré ou normalmente adensada? Por quê?
Normalmente adensada. A coesão é nula, indicando que não há estruturação do solo devido à
aplicação de tensões prévias.
1/4
Geotecnia II - Prova II - 23/06/2015
Prof. Flavio A. Crispim
Figura 02
Questão 3 (2,5).
As seguintes informações foram obtidas de testes de laboratório com amostras de uma
argila normalmente adensada saturada: (i) Um corpo de prova testado em ensaio de cisalhamento direto,
com tensão normal de 600 kPa, apresentou resistência ao cisalhamento de 350 kPa e (ii) Um corpo de
prova testado em ensaio de triaxial não drenado e adensado com 600 kPa, apresentou resistência ao
cisalhamento de 175 kPa.
a) (1,2) Determinar o ângulo de atrito efetivo da argila; ’ = 30º (ver Figura 03)
b) (1,3) Traçar a envoltória Mohr-Coulomb do solo e os círculos de Mohr para os casos (i) e (ii).
(ver Figura 03)
Figura 03
Questão 4 (2,5).
Sobre o perfil de argila siltosa mostrado na Figura 01 foi construído um aterro. Admitindo:
(i) tensões vertical e horizontal como tensões principais; (ii) K0 = 0,6 para argila siltosa; (iii) parâmetro de
poro-pressão A = 0,3 para argila siltosa; (iv) acréscimo de tensão vertical devido ao aterro, na profundidade
de 5 m, de 57 kPa e (v) acréscimo de tensão horizontal devido ao aterro, na profundidade de 5 m, de
19 kPa. Para o elemento de solo:
a) (1,0) Trace os caminhos de tensões totais e efetivas referentes à construção do aterro em condição
adensada e não drenada; (ver Figura 04)
b) (1,0) Trace os caminhos de tensões totais e efetivas referentes à construção do aterro em condição
não adensada e não drenada; (ver Figura 04)
c) (0,5) Determine a poro-pressão gerada com a construção do aterro em condição adensada e não
drenada.
u = 13 kPa (ver Figura 04)
2/4
Geotecnia II - Prova II - 23/06/2015
Prof. Flavio A. Crispim
Figura 01
Resolução
Condições iniciais
= . ℎ = 13.5 = 65
′ =
−
= 65 − 49 = 16
= ′ +
= 10 + 49 = 59
′ =
. ′ = 0,6.16 = 10
Condições finais
∆ = .∆
= . ( ′ − ′ ) = 0,3. (73 − 29) = 0,3.44 = 13
a) CU
3/4
Geotecnia II - Prova II - 23/06/2015
Prof. Flavio A. Crispim
Condições iniciais
′ =
=
+
2
−
2
16 + 10 26
=
= 13
2
2
16 − 10 6
=
= = 3
2
2
=
Condições finais
=
=
′ =
+
2
−
2
−
73 + 29 102
=
= 51
2
2
73 − 29 44
=
=
= 22
2
2
=
= 51 − 13 = 38
b) UU
Condições iniciais
=
=
′ =
+
2
−
2
−
65 + 59 124
=
= 62
2
2
65 − 59 6
=
= = 3
2
2
=
= 62 − 49 = 13
Condições finais
=
=
′ =
+
2
−
2
−
122 + 78 200
=
= 100
2
2
122 − 78 44
=
=
= 22
2
2
=
= 100 − (49 + 13) = 38
Figura 04
4/4