1 2a Lista de Exercícios Potencial Elétrico

1
2a Lista de Exercícios
Potencial Elétrico - Capacitância e Dielétricos Corrente e Resistência - Circuitos Elétricos
circunferência. A interseção da superfície equipotencial
de 5, 0 V com o plano xy também é uma circunferência?
1. Em um relâmpago típico, a diferença de potencial
entre os pontos de descarga corona é cerca de 109 V e
a quantidade de carga transferida é cerca de 30 C. (a)
Quanta energia é liberada? (b) Se toda a energia que
foi liberada pudesse ser usada para acelerar um carro de
1000kg que partiu do repouso, qual seria sua velocidade
final? (c) Que quantidade de gelo a 0o C seria possível
derreter se toda a energia liberada pudesse ser usada
para esse fim? O calor de fusão do gelo é 3, 3 × 105 J/kg.
2. O campo elétrico no interior de uma esfera não
condutora de raio R está radialmente direcionado e
tem módulo dado por E = Kqr/R3 , onde q é a carga
total da esfera (que é uniformemente distribuída) e r é
a distância ao centro. (a) Determine o potencial V (r),
supondo que V = 0 no centro da esfera. (b) Qual é a
diferença de potencial elétrico entre um ponto situado
na superfície da esfera e um no centro da esfera? Sendo
q positivo, qual deles está no potencial mais alto?
3. Considere dois pontos A e B e uma carga pontual
q de 1µC. Calcule a diferença de potencial entre esses
pontos nas duas situações (a) e (b) da figura 1. Você
esperava esses resultados? Por quê?
1m
2m
A
(a)
Figura 2: Exercício 6.
7. Duas grandes placas de metal, paralelas entre si e afastadas por uma distância igual a 1, 5cm,
possuem cargas iguais e de sinais contrários sobre
suas superfícies.
A placa carregada negativamente
está ligada a Terra e seu potencial é tomado como
zero. Se o potencial no meio da distância entre as placas
for igual a 5, 0 V , qual será o campo elétrico nesta região?
8. Seja λ a carga por unidade de comprimento distribuída uniformemente ao longo de um segmento de reta
de comprimento L. Determine o potencial no ponto P da
figura 3. Use esse resultado para calcular o componente
do campo elétrico nessa direção.
B
q
2m
q
B
λ
(b)
P
L
1m
s
A
Figura 3: Exercício 8.
Figura 1: Exercício 3.
4. Considere uma carga pontual de 15nC. Detemine
o raio da equipotencial que tem um potencial de 30V .
Estão igualmente espaçadas as superfícies cujos potenciais diferem de uma quantidade constante?
R
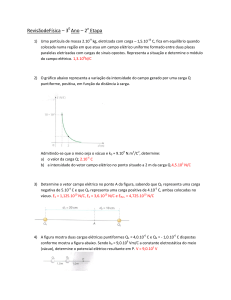
5. Usando V = kdq/r, calcule o potencial elétrico
criado por um anel carregado, de raio R, num ponto ao
longo do eixo que passa pelo centro do anel. A partir
dessa expressão para o potencial, ache a componente do
campo elétrico nessa direção.
6. Uma carga pontual q1 = +6e é mantida fixa na
origem de um sistema de coordenadas retangular; uma
segunda carga pontual q2 = −10e é mantida fixa no ponto
x = 8, 6nm e y = 0. Mostre que o lugar dos pontos no
plano xy para os quais V = 0 (além do infinito) é uma
circunferência com centro no eixo x, como mostrado na
figura 2. Determine a posição xc do centro e o raio R da
9. (a) Determine a expressão VAB = VA − VB para a
situação descrita na figura 4. (b) Verifique se o resultado
obtido se reduz aos valores esperados quando d = 0; a =
0; q = 0.
a
q
d
A
a
B
−q
Figura 4: Exercício 9.
10. Duas cargas de 2µC estão fixas no espaço e separadas pela distância de 2cm, como indicado na figura 5.
(a) Qual o valor do potencial elétrico no ponto C? (b)
traga uma terceira carga de 2µC, lentamente, desde o infinito até o ponto C. Quanto trabalho deve ser realizado
para isto? (c) Qual a energia potencial da configuração
quando a terceira carga está no ponto C?
2
C
ponto médio da base, considerendo q = 7, 0µC.
d/2
d/2
q
q
d/2
q
Figura 5: Exercício 10.
11. No retângulo da figura 6, os lados têm 5, 0cm e
15, 0cm de comprimento, enquanto que as cargas valem
q1 = −5, 0µC e q2 = 2, 0µC. (a) Qual o valor do potencial elétrico nos pontos A e B? (b) Que trabalho é
necessário para se mover uma terceira carga de 3, 0µC do
ponto B ao ponto A ao longo da diagonal do retângulo?
q1
A
B
q2
Figura 6: Exercício 11.
12. Uma partícula de carga q é mantida fixa num
ponto P e uma segunda partícula de massa m com
mesma carga q, está inicialmente em repouso a uma
distância r1 de P . A segunda partícula é, então, liberada
sendo repelida pela primeira. Determine a sua velocidade no instante em que ela se encontra a uma distância
r2 de P . Dados: q = 3, 1µC; m = 20mg; r1 = 0, 90mm;
r2 = 2, 5mm.
13. Considere duas esferas condutoras separadas, 1
e 2, sendo que a segunda tem o dobro do diâmetro da
primeira. Inicialmente, a esfera menor tem uma carga
positiva q, e a maior está descarregada. Vamos supor
que as esferas sejam ligadas por um fio fino e muito
comprido. (a) Qual é o valor do potencial de cada
esfera? (b) Determine as cargas finais sobre cada esfera.
14.
Um campo elétrico uniforme de magnitude
250V /m está na direção x poitiva. Uma carga de 12µC
se desloca da origem para o ponto (x, y) = (10cm, 50cm).
Calcule a variação na energia potencial desse sistema
carga-campo e a diferença de potencial na qual a carga
se desloca.
15. O potencial numa região entre x = 0m e x = 6m
é dado por V = a + bx, onde a = 10, 0V e b = −7, 0V /m.
Dertermine o potencial em x = 0, 3m e 6m. Determine
também a magnitude do campo elétrico nestes três
pontos.
16. As três cargas da figura 7 estão nos vértices de
um triângulo isósceles. Calcule o potencial elétrico no
4cm
−q
2cm
−q
Figura 7: Exercício 16.
17. Um condutor esférico tem um raio de 14, 0cm e a
carga de 26µC. Calcule o campo elétrico e o potencial
elétrico em r = 10, 0cm, r = 20cm e r = 14cm a partir
do centro da esfera.
R
18. Usando V = kdq/r, (a) calcule o potencial
elétrico criado por um disco carregado, de raio R,
num ponto ao longo do eixo que passa pelo centro do
disco. A partir dessa expressão para o potencial, ache a
componente do campo elétrico nessa direção. Compare
o valor do campo com o valor obtido por integração
direta. (b) Refaça os cálculos supondo que o disco
esteja carregado com uma distribuição não uniforme
dada por σ = 5ρ em µC/m2 , onde ρ é a distância de
um elemento de carga sobre o disco até o centro do disco.
19. Um capacitor de placas paralelas possui placas
circulares de raio igual a 8, 2cm e separação de 1, 3mm.
(a) Determine sua capacitância. (b) Se aplicarmos uma
diferença de potencial de 120V , qual será o valor da
carga que surgirá sobre as placas?
20. A placa e o catodo de um diodo a vácuo têm
a forma de dois cilindros concêntricos, com o catodo
ocupando o cilindro central. O diâmetro do catodo
é igual a 1, 6mm e o da placa mede 18mm, sendo o
comprimento de ambos os elementos igual a 2, 4cm.
Calcule a capacitância do diodo.
21. Um capacitor de 6, 0µF está ligado em série
com outro capacitor de 4, 0µF . Uma diferença de
potencial de 200V é aplicada a combinação. (a) Calcule
a capacitância equivalente. (b) Qual o valor da carga
sobre cada capacitor? (c) Determine a diferença de
potencial entre as placas de cada capacitor.
22. Resolva o problema anterior considerando que os
capacitores sejam ligados em paralelo.
23. (a) Três capacitores são ligados em paralelo.
Cada um deles possue placas de área A e separação
d entre as placas. Calcule a distância entre as placas
3
de um único capacitor com placa de área A, se a sua
capacitância for igual a da combinação paralela. (b)
Qual será a distância se os três capacitores estiverem
ligados em série?
24. Um capacitor de 100pF é carregado até atingir
uma diferença de potencial de 50V , mas, logo após,
a bateria que o carregou é retirada. O capacitor é,
então, ligado em paralelo com um segundo capacitor
que, inicialmente, está descarregado. Se a diferença de
potencial cair para 35V , qual será a capacitância do
segundo capacitor?
25. Quando giramos a chave S da figura 8 para a
esquerda, as placas do capacitor C1 adquirem uma diferença de potencial Vo . Inicialmente, C2 e C3 estão descarregados. A chave S é, agora, girada para a direita.
Quais os valores das cargas finais sobre os capacitores
correspondentes?
S
C2
Vo
C1
calcule a razão da energia armazenada antes e depois da
introdução da placa. (c) Quanto trabalho é realizado
sobre a placa quando esta é introduzida?
d
COBRE
b
Figura 9: Exercício 29.
30. Um capacitor de placas paralelas contém dois dielétricos diferentes, como mostrado na figura 10, cada
um ocupando metade da separação entre as placas.
Mostre que
de sua capacitância é dado por
o valor
k2
.
C = 2εdo A kk11+k
2
C3
A
Figura 8: Exercício 25.
26. Um determinado capacitor é submetido a um
potencial V . Havendo um aumento de 10% na energia
armazenada, qual a porcentagem de aumento no potencial V ?
27. Um capacitor é carregado até que a sua energia
armazenada seja igual a 4, 0J. Um segundo capacitor
descarregado é, então, ligado ao primeiro em paralelo.
(a) Se a carga se distribuir igualmente, qual será a
energia total acumulada nos campos elétricos? (b) Para
onde foi o restante da energia?
28. Uma certa substância possui uma constante dielétrica de valor 2, 8 e uma rigidez dielétrica de 18M V /m.
Se usarmos essa substância como material dielétrico a
ser introduzido num capacitor de placas paralelas, qual
será a área mínima que as placas do capacitor devem ter
para que a sua capacitância seja de 7, 0 × 10−2µF e para
que o capacitor seja capaz de resistir a uma diferença de
potencial de 4, 0kV ?
29. Uma placa de cobre de espessura b é introduzida
exatamente no meio e entre as placas de um capacitor
de placas planas e paralelas como é mostrado na figura
9. (a) Qual o valor da capacitância depois da introdução
das placas? (b) Se a carga for mantida entre as placas,
k1
k2
d
Figura 10: Exercício 30.
31.
Um campo elétrico uniforme de magnitude
3000V /m existe dentro de uma certa região. Que volume
de espaço contém uma energia total igual a 1, 0 × 10−7J?
32. (a) Quanta carga pode ser colocada em um
capacitor com ar entre as placas antes que ele sofra um
rompimento dielétrico se a área da placa é 5, 0cm2 ? (b)
Encontre a carga máxima se o poliestireno for utilizado
entre as placas em vez do ar.
33. Uma corrente de 5, 0A percorre um resistor de
10Ω durante o tempo de 4, 0min. Quantos coulombs e
quantos elétrons passam através da seção transversal do
resistor durante este intervalo de tempo?
34.
Considere uma esfera condutora isolada de
10cm de raio. Um fio transporta para dentro dela uma
corrente de 1, 0000020A. Um outro fio transporta uma
corrente de 1, 0000000A para fora da esfera. Quanto
tempo levaria para a esfera sofrer um aumento de 1000V
no potencial?
4
35. (a) A densidade de corrente por unidade de
área que atravessa um condutor cilíndrico de raio R
varia de acordo com a equação J = Jo (1 − r/R), onde
r é a distância a partir do eixo central. Desse modo,
a densidade de corrente Jo é máxima no eixo r = 0 e
descresce linearmente para zero na superfície r = R.
Calcule a corrente em termos de Jo e da área da seção
transversal do condutor A. (b) Suponha agora que a
densidade de corrente é máxima na superfície e decresce
linearmente para zero no eixo, assim J = Jo r/R. Calcule
a corrente.
36. Um fio condutor tem um diâmetro de 1, 0mm,
um comprimento de 2, 0m e uma resistência de 50mΩ.
Qual é a resistividade do mateiral?
37. Um condutor, cuja extensão é de 4m e cujo
diâmetro é 6mm, tem uma resistência de 15mΩ. Se uma
d.d.p. de 23V for aplicada em suas extremidades, qual
será a corrente através do condutor e a densidade de
corrente? Você pode identificar o material do qual este
condutor é feito?
38. Um fio de nicromo (liga níquel-cromo-ferro) tem
1, 0m de comprimento e 1, 0mm2 de área de seção transversal. Ao aplicarmos uma d.d.p. de 2, 0V entre as
suas extremidades, ele transporta uma corrente de 4, 0A.
Sendo a condutividade de um material definida como o
inverso de sua resistividade, calcule a condutividade do
nicromo.
39. Dois condutores são feitos do mesmo material
e têm o mesmo comprimento. O condutor A é sólido
e tem 1, 0mm de diâmetro. O condutor B é um tubo
oco de diâmetro interno de 1, 0mm e diâmetro externo
de 2, 0mm. Quanto vale a razão entre as resistências
medidas entre as suas extremidades?
7, 0W e o deixou ligado das 9h às 14h. Que quantidade
de carga passou através dele?
44. Um resistor cilíndrico, de raio igual a 5, 0mm e de
comprimento igual a 2, 0cm é feito de um material cuja
resisitividade é de 3, 5 × 10−5Ωm. Quais são a densidade
de corrente e a diferença de potencial quando a potência
dissipada é de 1, 0W ?
45. Uma esfera pequena que tem uma carga q gira
em um círculo na extremidade de um fio isolante. A
freqüência angular de rotação é ω. Qual é a corrente
média representada por esta carga em rotação?
46. A quantidade de carga que atravessa uma superfície de área 2, 00cm2 varia no tempo de acordo com
q = 4t3 + 5t + 6, com t em segundos e q em coulomb.
Calcule a corrente e a densidade de corrente através
desta área no instantne de tempo de 1, 0s.
47. Suponha que a corrente num condutor diminua
exponencialmente com o tempo de acordo com a equação
I(t) = Io e−t/τ , onde Io é a condição inicial e τ é uma
constante com dimensões de tempo. Considere um ponto
de observação fixo dentro do condutor. (a) Quanta
carga passa por este ponto entre t = 0 e t = τ ? (b)
E entre t = 0 e t = 10τ ? (c) Quanta carga deve ter
passado se esperarmos t → ∞?
48. Uma d.d.p. de 0, 9V é mantida em um fio de
tungstênio de 1, 50m de comprimento que tem uma área
de seção transversal de 0, 6mm2 . Qual é a corrente no fio?
40. Uma barra de alumínio quadrada tem 1, 3m
de comprimento e 5, 2mm de aresta. (a) Calcule a
resistência entre as duas extermidades. (b) Qual deverá
ser o diâmetro de uma barra de cobre circular com 1, 3m
de comprimento, se a resistência das barras for a mesma?
49. Uma certa torradeira tem um elemento aquecedor
feito de um fio de resistência de nicromo. Quando a
torradeira é ligada primeiramente a 120V (e o fio está
a uma temperatura de 20o C), a corrente inicial é de
1, 80A. Contudo, a corrente começa a diminuir à medida
que o elemento resistivo se aquece. Quando a torradeira
atinge uma temperatura operacional final, a corrente
caiu para 1, 53A. (a) Encontre a potência fornecida
quando a torradeira está a sua temperautra operacional.
(b) Qual é a temperatura final do elemento aquecedor?
41. Um cabo elétrico consiste em 125 fios de um
condutor delgado, sendo que cada um tem uma resistência de 2, 65µΩ. A mesma d.d.p. é aplicada entre
as extremidades de cada fio e resulta numa corrente
total de 0, 75A. (a) Calcule a corrente em cada fio. (b)
Determine a diferença de potencial que foi aplicada. (c)
Qual é a resistência do cabo?
50. Um carro elétrico é projetado para utilizar
um conjunto de baterias de 12, 0V com um total de
armazenagem de energia de 2, 00 × 107J. (a) Se o motor
elétrico utiliza 8, 00kW , qual é a corrente no motor?
(b) Se o motor elétrico utiliza 8, 00kW quando o carro
se desloca a uma velocidade constante de 20, 0m/s, que
distância o carro percorre antes de ficar sem combustível?
42. Quando uma d.d.p. de 115V é aplicada através de um condutor cujo comprimento mede 10m e
cujo raio é de 0, 30mm, a densidade de corrente é igual
a 1, 4×104 A/m2 . Determine a resistividade do condutor.
51. O cobre e o alumínio estão sendo considerados
para uma linha de transmissão de alta voltagem que
deve carregar uma corrente de 60A. A resistência
por unidade de comprimento é de 0, 15Ω/km. Calcule
para cada opção do material do cabo: (a) a densidade de corrente e (b) a massa por metro de cabo. As
43. Um estudante pegou seu rádio portátil de 9, 0V e
5
densidades do cobre e do alumínio são 8960 e 2700kg/m3.
52. Na figura 11, que valor terá R se a corrente no
circuito tiver 1, 0mA? Considere ε1 = 2, 0V ; ε2 = 3, 0V ;
r1 = r2 = 3, 0Ω. Qual a taxa na qual a energia térmica
aparece em R?
57. (a) Calcule a intensidade das três correntes que
aparecem no circuito da figura 13. (b) Calcule Vab . Considere R1 = 1, 0Ω; R2 = 2, 0Ω; ε1 = 2, 0V e ε2 = ε3 =
4, 0V .
a
R1
E1
E2
r2
r1
R1
R2
E1
E3
E2
R1
b
R1
Figura 13: Exercício 57.
R
Figura 11: Exercício 52.
53. A corrente em um circuito de uma única malha
tem 5, 0A. Quando uma resistência adicional de 2, 0Ω é
inserida em série, a corrente cai para 4, 0A. Qual era a
resistência no circuito original?
54. Uma bateria solar gera uma d.d.p. de 0, 10V ,
quando um resistor de 500Ω é conectado a ela, e uma
d.d.p. de 0, 15V , quando o resistor é substituído por
um outro de 1000Ω. Quais são a resistência e a fem
da bateria solar? A área da bateria é de 5, 0cm2 e a
intensidade da luz é de 2, 0mW/cm2 . Qual é a eficiência
da bateria ao converter a energia luminosa em calor,
tendo o resistor externo 1000Ω?
55. Na figura 12, calcule o valor da corrente em cada
um dos resistores e a d.d.p. entre os pontos a e b. Considere: ε1 = 6, 0V ; ε2 = 5, 0V ; ε3 = 4, 0V ; R1 = 100Ω e
R2 = 50Ω.
58. Na figura 14, (a) calcule a potência que aparece
como energia térmica em R1 , R2 e R3 . (b) Calcule as
potências fornecidas por ε1 e ε2 . Suponha que ε1 = 3, 0V ;
ε2 = 1, 0V ; R1 = 5, 0Ω; R2 = 2, 0Ω e R3 = 4, 0Ω.
R2
R3
E1
R1
E2
Figura 14: Exercício 58.
59. A figura 15 mostra uma bateria ligada a um resistor uniforme Ro . Um contato deslizante pode mover-se
através do resistor de x = 0 até x = 10cm à esquerda.
Ache uma expressão para a potência dissipada no resistor R como função de x. Faça o gráfico da função para
ε = 50V ; R = 2000Ω e Ro = 100Ω.
R
x
Ro
E1
E2
a
E3
R2
b
E
Figura 15: Exercício 59.
R1
Figura 12: Exercício 55.
56. Duas lâmpadas, uma de resistência R1 e a outra
de resistência R2 (R2 < R1 ) estão ligadas: (a) em
paralelo e (b) em série. Qual é a lâmpada mais brilhante
em cada caso?
60. Um capacitor de 1, 0µF e energia inicialmente armazenada de 0, 50J é descarregado através de um resistor
de 1, 0M Ω. (a) Qual a carga inicial do capacitor? (b)
Qual o valor da corrente através do resistor no momento
em que a descarga se inicia? (c) Determine VC , a voltagem através do capacitor, e VR , a voltagem através do
resistor em função do tempo. (d) Expresse a taxa de geração de energia térmica no resistor em função do tempo.
6
61. Um capacitor C inicialmente descarregado é
totalmente carregado por uma fem de valor constante
em série com um resistor R. (a) Mostre que a energia
final armazenada no capacitor é metade da energia
fornecida pela fem. (b) Por integração direta de i2 R
sobre o tempo de carga, mostre que a energia térmica
dissipada pelo resistor também é metade da energia
fornecida pela fem.
62. Uma bateria tem uma fem de 15, 0V . A voltagem
entre os terminais da bateria é de 11, 6V quando ela
está fornecendo 20, 0W de potência para um resistor de
carga externo R. Determine o valor de R e o valor da
resistência da bateria.
63. No circuito da figura 16, a chave S fivou aberta
por muito tempo. Ela é, então, subitamente fechada.
Determine a constante de tempo (a) antes de a chave ser
fechada e (b) após a chave ser fechada. (c) Se a chave
for fechada em t = 0, determine a corrente na chave como
função do tempo.
Figura 16: Exercício 63.
RESPOSTAS
1.
2.
3.
4.
6.
7.
8.
3 × 1010 J; 7, 75km/s; 9 × 104 kg
−q
−qr 2
8πεo R3 ; 8πεo R
VAB = 4, 5 × 103 V
4, 5m
xc = −4, 8nm; R = 8, 1nm; Não.
667N/C λ
L
s
λ
ln
− 4πε
L+s ; 4πεo s(L+s)
o
qd
9. 2πεo a(a+d)
11. −7, 8 × 105 V ; 0, 6 × 105 V ; 2, 5J
12. 2, 48km/s
13. V1 = V2 ; q1 = q/3; q2 = 2q/3
14. −0, 3mJ
15. 10V , −11V , −32V ; 7N/C na direção +x
16. −12M V
19. 144pF ; 17, 3nC
20. 0, 551pF
21. 2, 4µF ; 480µC; 80V ; 120V
22. 10µF ; 1200µC; 800µC; 200V
23. d′ = d/3; d′ = 3d
24. 43pF
C2 +C1 C3
25. q1 = C1 CC21+C
C1 Vo ;
2 C3 +C3 C1
C2 C3
C1 Vo
q2 = q3 = C1 C2 +C
2 C3 +C3 C1
26. 4, 88%
27. 2, 0J
28. 0, 63m2
−q2 b
εo A
d
; d−b
; 2ε
29. d−b
oA
31. 2, 51l
32. 13, 3nC; 272nC
33. 1200C; 7, 5 × 1021
34. 5, 6ms
35. Jo A/3; 2Jo A/3
36. 1, 96 × 10−8 Ωm
−1
38. 2, 0 × 106 (Ωm)
41. 6, 00mA; 1, 59 × 10−8 V ; 21, 2nΩ
42. 8, 21 × 10−4 Ωm
43. 14kC
45. qω
2π
47. 0, 632Ioτ ; 0, 99995Ioτ ; Io τ
48. 6, 43A
49. 184W ; 461oC
50. 667A; 50, 0km
51. 5, 32 × 105 A/m2 e 1, 01kg/m para o cobre. 3, 27 ×
105 A/m2 e 0, 495kg/m para o alumínio
52. 990Ω; 9, 4 × 10−4 W
53. 8Ω
54. 1000Ω; 300mV
55. i1 = 50mA; i2 = 60mA; Vab = 9V
56. r2 ; r1
57. ramo esquerdo: 0, 67A para baixo; ramo central:
0, 33A para cima; ramo direito: 0, 33A para cima; 3, 3V
2
x
, x em cm
59. 50kW 2000+10x−x
2
60. 1mC; 1mA; VC = 1000e−t; VR = −1000e−t
62. 6, 73Ω; 1, 97Ω
63. 1, 50s; 1, 00s; 200µA + (100µA) e−t/1,00s