UESPI – Campus Prof. Alexandre Alves de Oliveira Disciplina

UESPI – Campus Prof. Alexandre Alves de
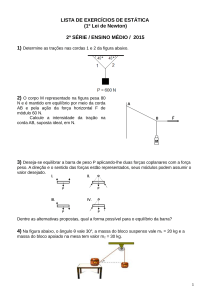
Oliveira
Disciplina: Física 1 – 90h
Curso: Bach. em Ciência da Computação
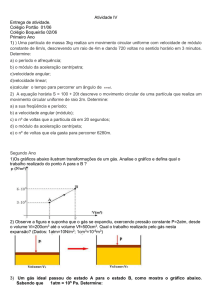
Prof. Olímpio Sá
Aluno:
Segunda Avaliação Semestral
Bloco: 3
Nota
Data:
15/04/2014
INSTRUÇÕES:
a) Esta prova é individual, não sendo permitida cópia entre os presentes.
b) A prova contém 6 (seis) questões dissertativa. A prova é para ser feita em casa e
entregue na data que está no site do curso.
c) Não deixe as respostas rasuradas.
d) O professor não considerará as provas entregues após o dia e horário fixado para a
entrega da avaliação.
QUESTÕES:
1. (1,5 pontos) [Moysés]: Um par de cargas puntiformes +2 q e –q estão separadas
por uma distância l. Mostre que a superfície equipotencial V=0 é uma esfera e
determine o seu centro e raio?
2. (2,0 pontos) [Moysés]: Uma esfera de raio R está uniformemente carregada,
com carga total q. (a) Determine o potencial V em pontos internos e externos à
esfera e trace um gráfico de V em função da distância ao centro. (b) Tomando
q=-e, com uma carga puntiforme +e no centro da esfera como modelo para o
átomo de hidrogênio, qual é a expressão do potencial neste caso?
3. (1,5 pontos) [Moysés]: Determine a energia potencial de uma carga puntiforme
arbitrária num certo ponto de um campo eletrostático uniforme.
4. (1,5 pontos) Em relação a dipolo elétrico:
(a) Defina?
(b) Derive o potencial elétrico?
(c) Como fica sua energia potencial quando ele está em um campo uniforme?
5. (1,5 pontos) Derive a capacitância de um capacitor cilíndrico no vácuo?
6. (2,0 pontos) [Moysés]: O espaço entre as placas (de área A) de um capacitor
plano está preenchido por duas camadas dielétricas adjacentes, de espessuras d1
e d2 e constantes dielétricas κ1 e κ2, respectivamente. A diferença de potencial
entre as placas é V e o campo aponta de 1 para 2. Ache:
(a) A capacitância C do capacitor?
(b) A densidade superficial de carga livre σ nas placas?
Bom Proveito!