LISTA de RECUPERAÇÃO MATEMÁTICA

LISTA de RECUPERAÇÃO
O
Recuperação: 2 ANO
MATEMÁTICA
Professor:
ARGENTINO
DATA: 01 / 05 / 2016
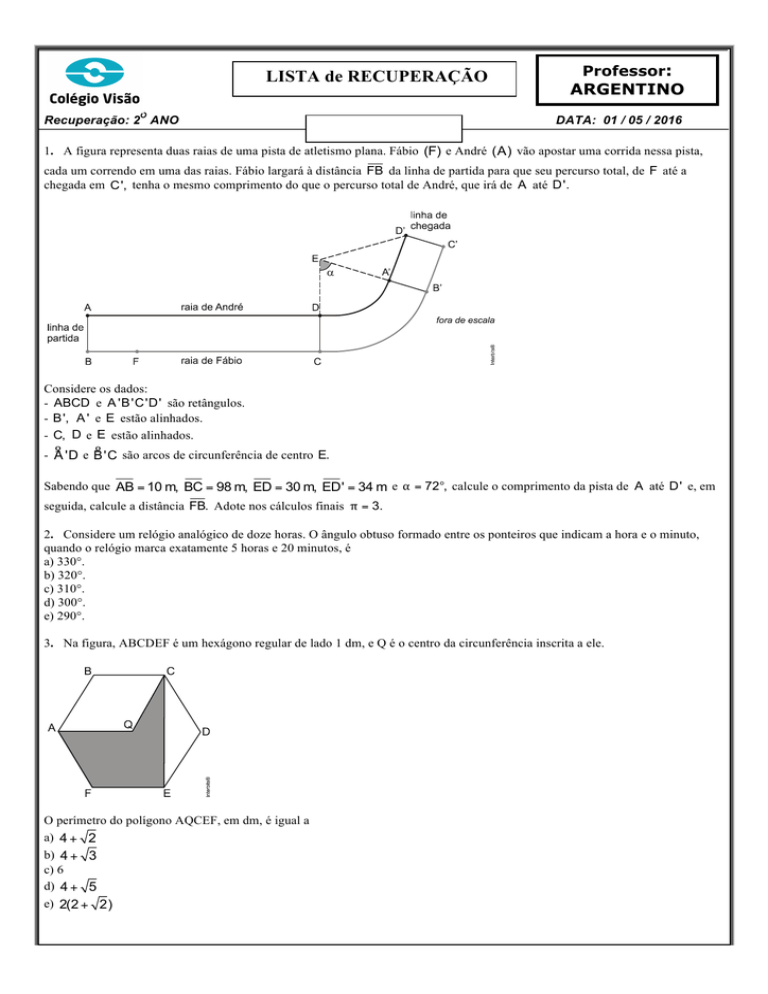
1. A figura representa duas raias de uma pista de atletismo plana. Fábio (F) e André (A) vão apostar uma corrida nessa pista,
cada um correndo em uma das raias. Fábio largará à distância FB da linha de partida para que seu percurso total, de F até a
chegada em C', tenha o mesmo comprimento do que o percurso total de André, que irá de A até D'.
Considere os dados:
- ABCD e A 'B'C'D' são retângulos.
- B', A ' e E estão alinhados.
- C, D e E estão alinhados.
º 'D e B'C
º
- A
são arcos de circunferência de centro E.
Sabendo que AB = 10 m, BC = 98 m, ED = 30 m, ED' = 34 m e α = 72°, calcule o comprimento da pista de A até D' e, em
seguida, calcule a distância FB. Adote nos cálculos finais π = 3.
2. Considere um relógio analógico de doze horas. O ângulo obtuso formado entre os ponteiros que indicam a hora e o minuto,
quando o relógio marca exatamente 5 horas e 20 minutos, é
a) 330°.
b) 320°.
c) 310°.
d) 300°.
e) 290°.
3. Na figura, ABCDEF é um hexágono regular de lado 1 dm, e Q é o centro da circunferência inscrita a ele.
O perímetro do polígono AQCEF, em dm, é igual a
a) 4 + 2
b) 4 + 3
c) 6
d) 4 + 5
e) 2(2 + 2)
1
4. Uma família viaja para Belém (PA) em seu automóvel. Em um dado instante, o GPS do veículo indica que ele se localiza nas
seguintes coordenadas: latitude 21°20’ Sul e longitude 48°30’ Oeste. O motorista solicita a um dos passageiros que acesse a
Internet em seu celular e obtenha o raio médio da Terra, que é de 6730 km, e as coordenadas geográficas de Belém, que são latitude
1°20’ Sul e longitude 48°30’ Oeste. A partir desses dados, supondo que a superfície da Terra é esférica, o motorista calcula a
distância D, do veículo a Belém, sobre o meridiano 48°30’ Oeste.
Assinale a alternativa que apresenta, corretamente, o valor da distância D, em km.
π
a) D = 6730
9
π
b) D =
( 6730 )2
18
π
c) D =
6730
9
π
d) D =
6730
36
2
⎛π⎞
e) D = ⎜ ⎟ 6730
⎝3⎠
5. Se o relógio da figura marca 8 h e 25 min, então o ângulo x formado pelos ponteiros é
a) 12° 30’.
b) 90°.
c) 102° 30’.
d) 120°.
6. A caminhada é uma das atividades físicas que, quando realizada com frequência, torna-se eficaz na prevenção de doenças
crônicas e na melhora da qualidade de vida.
Para a prática de uma caminhada, uma pessoa sai do ponto A, passa pelos pontos B e C e retorna ao ponto A, conforme trajeto
indicado na figura.
Quantos quilômetros ela terá caminhado, se percorrer todo o trajeto?
a) 2,29.
b) 2,33.
c) 3,16.
d) 3,50.
e) 4,80.
7. Os lados de um losango medem 4 e um dos seus ângulos 30°. A medida da diagonal menor do losango é
a) 2 2 − 3 .
b)
2 + 3.
2
c) 4 2 − 3 .
d) 2 2 + 3 .
e) 4 2 + 3 .
8. Um professor de geografia forneceu a seus alunos um mapa do estado de São Paulo, que informava que as distâncias
aproximadas em linha reta entre os pontos que representam as cidades de São Paulo e Campinas e entre os pontos que representam
as cidades de São Paulo e Guaratinguetá eram, respectivamente, 80km e 160km. Um dos alunos observou, então, que as
distâncias em linha reta entre os pontos que representam as cidades de São Paulo, Campinas e Sorocaba formavam um triângulo
equilátero. Já um outro aluno notou que as distâncias em linha reta entre os pontos que representam as cidades de São Paulo,
Guaratinguetá e Campinas formavam um triângulo retângulo, conforme mostra o mapa.
Com essas informações, os alunos determinaram que a distância em linha reta entre os pontos que representam as cidades de
Guaratinguetá e Sorocaba, em km, é próxima de
a) 80 ⋅ 2 + 5 ⋅ 3
b) 80 ⋅ 5 + 2 ⋅ 3
c) 80 ⋅ 6
d) 80 ⋅ 5 + 3 ⋅ 2
e) 80 ⋅ 7 ⋅ 3
9. O valor de cos (2 280°) é
1
2
a) − .
b)
1
.
2
2
.
2
3
d) −
.
2
3
e)
.
2
c) −
10. O relógio Tower Clock, localizado em Londres, Inglaterra, é muito conhecido pela sua precisão e tamanho. O ângulo interno
formado entre os ponteiros das horas e dos minutos deste relógio, desprezando suas larguras, às 15 horas e 20 minutos é:
π
12
π
b)
36
a)
3
π
6
π
d)
18
π
e)
9
c)
11. Uma praça circular de raio R foi construída a partir da planta a seguir:
Os segmentos AB, BC e CA simbolizam ciclovias construídas no interior da praça, sendo que AB = 80 m. De acordo com a
planta e as informações dadas, é CORRETO afirmar que a medida de R é igual a:
a)
b)
c)
d)
e)
160 3
m
3
80 3
m
3
16 3
m
3
8 3
m
3
3
m
3
12. Na figura estão posicionadas as cidades vizinhas A, B e C, que são ligadas por estradas em linha reta. Sabe-se que, seguindo
por essas estradas, a distância entre A e C é de 24 km, e entre A e B é de 36 km.
Nesse caso, pode-se concluir que a distância, em km, entre B e C é igual a
a) 8 17.
b) 12 19.
c) 12 23.
d) 20 15.
e) 20 13.
13. Para representar os harmônicos emitidos pelos sons dos instrumentos da orquestra, usam-se funções trigonométricas.
A expressão 2 sen2 x + 2 cos2 x – 5 envolve estas funções e, para π < x <
a) –7
b) –3
4
3π
, seu valor de é:
2
c) –1
d) 2 π – 5
e) 3 π – 5
14. Um satélite orbita a 6.400 km da superfície da Terra. A figura abaixo representa uma seção plana que inclui o satélite, o centro
da Terra e o arco de circunferência AB. Nos pontos desse arco, o sinal do satélite pode ser captado. Responda às questões abaixo,
considerando que o raio da Terra também mede 6.400 km.
a) Qual o comprimento do arco AB indicado na figura?
b) Suponha que o ponto C da figura seja tal que cos(θ) = 3 / 4. Determine a distância d entre o ponto C e o satélite.
15. Um topógrafo deseja calcular a distância entre pontos situados à margem de um riacho, como mostra a figura a seguir. O
topógrafo determinou as distâncias mostradas na figura, bem como os ângulos especificados na tabela abaixo, obtidos com a ajuda
de um teodolito.
Visada
^
A CB
^
BCD
^
A BC
Ângulo
π
6
π
3
π
6
a) Calcule a distância entre A e B.
b) Calcule a distância entre B e D.
16. a) Determine o perímetro do triângulo na forma decimal aproximada, até os décimos. Se quiser, use algum destes dados:
352 = 1225 ; 362 = 1296 ; 372 = 1369 .
5
b) Um aluno tinha de fazer um cartaz triangular, em cartolina. Decidiu construir o triângulo com as seguintes medidas dos lados:
6 cm , 8 cm , e 16 cm . Ele conseguirá fazer o cartaz? Por quê?
17. Laura decidiu usar sua bicicleta nova para subir uma rampa. As figuras a seguir ilustram a rampa que terá que ser vencida e a
bicicleta de Laura.
a) Suponha que a rampa que Laura deve subir tenha ângulo de inclinação á, tal que cos(á) =
0,99 . Suponha, também, que cada
pedalada faça a bicicleta percorrer 3,15 m. Calcule a altura h (medida com relação ao ponto de partida) que será atingida por
Laura após dar 100 pedaladas.
b) O quadro da bicicleta de Laura está destacado na figura à direita. Com base nos dados da figura, e sabendo que a mede 22 cm,
calcule o comprimento b da barra que liga o eixo da roda ao eixo dos pedais.
18. Suponha que o planeta Terra seja uma esfera de centro C e raio R. Na figura, está representado o planeta Terra e uma nave
espacial N. A fração visível da superfície da Terra por um astronauta na nave N é dada em função do ângulo ‫ט‬, mostrado na figura,
pela expressão:
f (θ) =
1 − senθ
2
a) Determine o ângulo θ , em graus, para o qual é visível da nave a quarta parte da superfície da Terra e a distância da nave à
superfície da Terra neste caso. (Use a aproximação R = 6.400 km.)
b) Se um astronauta numa nave, a uma distância d da Terra, avista a superfície da Terra com ângulo θ = 15o, determine a fração
visível da superfície da Terra pelo astronauta. (Use as aproximações
2 = 1,4 e 6 = 2,4 .)
19. Na ilustração a seguir, a casa situada no ponto B deve ser ligada com um cabo subterrâneo de energia elétrica, saindo do ponto
A. Para calcular a distância AB, são medidos a distância e os ângulos a partir de dois pontos O e P, situados na margem oposta do
rio, sendo O, A e B colineares. Se OPA = 30°, POA = 30°, APB = 45° e OP = (3 + 3 )km, calcule AB em hectômetros.
6
20. Uma empresa de vigilância irá instalar um sistema de segurança em um condomínio fechado, representado pelo polígono da
figura a seguir.
A empresa pretende colocar uma torre de comunicação, localizada no ponto A, indicado na figura, que seja equidistante dos
vértices do polígono, indicados por P, Q, R, S e T, onde serão instalados os equipamentos de segurança. Sabe-se que o lado RQ
desse polígono mede 3000 m e as medidas dos outros lados são todas iguais à distância do ponto A aos vértices do polígono.
Calcule a distância do ponto A, onde será instalada a torre, aos vértices do polígono.
7
Gabarito:
Resposta da questão 1:
Se ABCD e A 'B'C'D' são retângulos e os percursos de Fábio e André têm o mesmo comprimento, então
º −A
º 'D
FB = B'C
2π
=
⋅ (40 − 30)
5
≅ 12 m.
Resposta da questão 2:
[B]
20
= 10°. Desse modo, o menor ângulo formado
2
pelos ponteiros dos minutos e das horas, às 5 horas e 20 minutos, é igual a 30° + 10° = 40°. Em consequência, o maior ângulo
formado por esses ponteiros é igual a 360° − 40° = 320°.
O ângulo percorrido pelo ponteiro das horas em 20 minutos corresponde a
Observação: Dizemos que um ângulo α é obtuso se 90° < α < 180°.
Resposta da questão 3:
[B]
Como EF = FA = AQ = QC = 1dm, basta calcularmos CE.
µ = 120° e CD = DE = 1dm, pela Lei dos Cossenos, obtemos
Sabendo que CDE
2
2
2
µ
CE = CD + DE − 2 ⋅ CD ⋅ DE ⋅ cosCDE
⎛ 1⎞
= 12 + 12 − 2 ⋅ 1⋅ 1⋅ ⎜ − ⎟
⎝ 2⎠
= 3.
Portanto, CE = 3 dm e o resultado pedido é
EF + FA + AQ + QC + CE = (4 + 3)dm.
Resposta da questão 4:
[A]
O arco percorrido pelo automóvel corresponde a um ângulo central cuja medida é
21°20 '− 1°20 ' = 20° ⋅
=
π
rad
180°
π
rad.
9
Portanto, sabendo que o raio da Terra mede 6.730 km, vem
D=
π
⋅ 6730km.
9
Resposta da questão 5:
[C]
8
O deslocamento do ponteiro das horas, em 25 minutos, é igual a
mede 3 ⋅ 30° = 90°, segue que
25
= 12°30'. Logo, como o ângulo entre as posições 5 e 8
2
x = 90° + 12°30' = 102°30'.
Resposta da questão 6:
[D]
Pela Lei dos Cossenos, obtemos:
2
2
2
µ
BC = AC + AB − 2 ⋅ AC ⋅ AB ⋅ cosBAC
= (0,8)2 + 12 − 2 ⋅ 0,8 ⋅ 1⋅ cos150°
⎛
3⎞
⎟
= 0,64 + 1 − 2 ⋅ 0,8 ⋅ ⎜ −
⎝ 2 ⎠
≅ 1,64 + 0,8 ⋅ 1,7
≅ 3.
Logo, BC ≅ 1,7 e, portanto, o resultado é 1 + 0,8 + 1,7 = 3,5.
Resposta da questão 7:
[C]
Considere a figura.
µ = 30°, pela Lei dos Cossenos, obtemos
Como AB = AD = 4 u.c. e BAD
2
2
2
µ
BD = AB + AD − 2 ⋅ AB ⋅ AD ⋅ cosBAD
= 42 + 42 − 2 ⋅ 4 ⋅ 4 ⋅
3
2
= 2 ⋅ 16 − 16 3.
Portanto,
BD = 4 2 − 3 u.c.
Resposta da questão 8:
[B]
Sejam S, P, G e C, respectivamente, os pontos que representam as cidades de Sorocaba, São Paulo, Guaratinguetá e Campinas.
9
$ = 60° e CPG
$ = 150°. Logo, aplicando a Lei dos Cossenos no triângulo SPG, encontramos
$ = 90°, vem SPG
Sabendo que SPC
2
2
2
$
SG = SP + PG − 2 ⋅ SP ⋅ PG ⋅ cosSPG
= 802 + 1602 − 2 ⋅ 80 ⋅ 160 ⋅ cos150°
⎛
3⎞
⎟
= 6400 + 25600 − 2 ⋅ 12800 ⋅ ⎜ −
⎜ 2 ⎟
⎝
⎠
= 6400 ⋅ (5 + 2 ⋅ 3)
Portanto, SG = 80 ⋅ 5 + 2 ⋅ 3 km.
Resposta da questão 9:
[A]
2280° = 360°.6 + 120°
1
2
Logo, cos (2 280°) = cos 120° = − .
Resposta da questão 10:
[E]
Considere a figura.
360°
= 30°. Logo, θ + α = 30°, sendo α o resultado pedido.
12
Por outro lado, como o ângulo θ corresponde ao deslocamento do ponteiro das horas, em 20 minutos, segue que
A cada 5 minutos corresponde um ângulo de
θ=
20min ⋅ 30°
= 10°.
60min
Desse modo,
10° + α = 30° ⇔ α = 20° =
π
rad.
9
Resposta da questão 11:
[B]
Pela Lei dos Senos, segue que:
AB
80
80 3 80 3
= 2R ⇔ 2R =
⇔R=
⋅
=
m.
sen60°
3
3
3 3
2
Resposta da questão 12:
[B]
10
Aplicando a Lei dos Cossenos, obtemos
2
2
2
µ ⇔
BC = AB + AC − 2 ⋅ AB ⋅ AC ⋅ cosBAC
2
⎛ 1⎞
BC = 362 + 242 − 2 ⋅ 36 ⋅ 24 ⋅ ⎜ − ⎟ ⇔
⎝ 2⎠
2
BC = 1296 + 576 + 864 ⇒
BC = 2736 = 12 19 km.
Resposta da questão 13:
[B]
2sen2x + 2cos2x - 5 = 2.(sen2x + cos2x) – 5 = 2.1 – 5 = - 3
Resposta da questão 14:
a) No triângulo assinalado:
R é a medida do raio da terra.
cos α =
R
1
= ⇒ α = 60°
R +R 2
Portanto, o arco AB mede 120° e seu comprimento será dado por:
2 ⋅ π ⋅ R 2 ⋅ π ⋅ 6400 12800 π
=
=
km.
3
3
3
b) Aplicando o teorema dos cossenos no triângulo assinalado, temos:
d2 = R2 + (2R)2 − 2.R.2R.cos θ
d2 = 5R2 − 4.R2 .(3/4)
d = 2.R2
d=R 2
d = 6400. 2 km
11
Resposta da questão 15:
a)
No triângulo ABC assinalado, temos:
152 = x 2 + x 2 − 2 ⋅ x ⋅ x ⋅ cos120°
⎛ 1⎞
225 = 2x 2 − 2x 2 ⎜ − ⎟
⎝ 2⎠
225 = 3x 2
x 2 = 75
x = 5 3m
b)
No triângulo BDC, temos:
12
y2 = 152 + 102 − 2 ⋅ 15 ⋅ 10 ⋅ cos60°
y2 = 225 + 100 − 150
y = 175
y = 5 7m
Resposta da questão 16:
a) Calculando a medida x do lado que falta temos:
x2 = 62 + 82 – 2 ⋅ 6 ⋅ 8 ⋅ cos60°
x=
52
x = 2 13
x ; 2 ⋅ 3,6 (de acordo com as aproximações dadas)
x ; 7,2
Portanto, o perímetro das figuras será dado por P = 6 + 8 + 7,2 = 21,2.
b) Não, pois 16 > 6 + 8 (a medida do lado de um triângulo deve ser menor que a medida dos outros dois).
Resposta
100 passos = 100. 3,15 = 315m
da
questão
a) Na figura 1
sen2α = 1 – cos2α
0,99 2
sen2α = 1 sen2α = 0,01
sen α = 1/100
1
h
=
⇔ h = 31,5m
10 315
b) na figura 2
logo
aplicando o teorema dos cossenos.
222 = b2 + b2 – 2b.b.
b2 =
22 2
.
3
2
2+ 3
1− 3 2 + 3
b = 22 2 .(2 + 3 )
b = 22 2 + 3 cm
13
17:
Resposta da questão 18:
a) Como θ é agudo, segue que:
1 1− sen θ
1
=
⇔ sen θ = ⇒ θ = 30°.
4
2
2
Do triângulo NAC, vem:
R
6400
sen θ =
⇒ sen30° =
⇒ d = 12800 − 6400 = 6.400km.
R+d
6400 + d
b) Para θ = 15°, segue que f(15°) =
Mas
sen15° = sen(45° − 30°)
1− sen15°
.
2
= sen 45° cos30° − sen30° cos 45°
=
2 3 1 2
⋅
− ⋅
2 2 2 2
6− 2
4
2,4 − 1,4
=
4
1
= .
4
Portanto,
1
1−
3
4
f(15°) =
= .
2
8
=
Resposta da questão 19:
De acordo com os dados do problema temos a figura.
14
3+ 3
o
sen120
=
y
o
sen30
⇔
3+ 3
=
2
3.y
⇔ y = 3 +1
2
O triângulo POB é isósceles logo, OB = 3 + 3
Portanto, AB = x = 3 + 3 −
(
)
3 + 1 = 2km = 20hm .
Resposta da questão 20:
Como AQ = AR = AS = AT = AP = RS = ST = TP = PQ, segue que os triângulos ARS, AST, ATP e APQ são equiláteros.
ˆ + SAT
ˆ + TAP
ˆ + PAQ
ˆ = 240° implica em: QAR
ˆ = 360° − 240° = 120°.
Logo, RAS
Aplicando a Lei dos Cossenos no triângulo QAR, obtemos:
2
2
2
ˆ ⇔
QR = AQ + AR − 2 ⋅ AQ ⋅ AR ⋅ cosQAR
2
2 ⎛ 1⎞
30002 = 2 ⋅ AQ − 2 ⋅ AQ ⋅ ⎜ − ⎟ ⇔
⎝ 2⎠
2
3 ⋅ AQ = 30002 ⇒
( 3 ⋅ AQ)2 = 30002 ⇒ AQ =
3000
= 1000 3 m.
3
Portanto, a distância do ponto A, onde será instalada a torre, aos vértices do polígono é: 1000 3 m.
15