Simulado EFOMM - Matemática

Simulado EFOMM - Matemática
1. Sejam X, Y, Z, W subconjuntos de N tais que:
1. (X – Y ) ∩ Z = {1, 2, 3, 4},
2. Y = {5, 6}, Z ∩ Y = ∅,
3. W ∩ (X – Z) = {7, 8},
4. X ∩ W ∩ Z = {2, 4}.
Então o conjunto
[X ∩ (Z ∪ W)] – [W ∩ (Y ∪ Z)]
é igual a
(A) {1, 2, 3, 4, 5}
(B) {1, 2, 3, 4, 7}
(C) {1, 3, 7, 8}
(D) {1, 3}
(E) {7, 8}.
2
e duas circunferência C1 e C2, centradas na origem. Sabe-se que C1
x
1
tangencia gráfico de f, e que um ponto de abscissa – pertence a C2 e ao gráfico de f. Nessas condições, a área da coroa
2
2. Considere a função real f, definida por f(x) = –
circular, definida por C1 e C2, é igual a
(A)
(B)
(C)
(D)
(E)
65
π
4
49
π
4
25
π
4
9
π
4
π
4
3. A soma das raízes da equação:
3 tg x -
que pertencem ao intervalo [0, 2 π ], é:
17π
(A)
4
16π
(B)
3
15π
(C)
3
14π
(D)
3
13π
(E)
.
4
3 sen 2x + cos 2x = 0,
4. Simplificando a expressão
⎛ 3π
⎞
⎛ 3π
⎞
sen ⎜
− x ⎟ + cos(4 π − x ) + tg ⎜
− x⎟
⎝ 2
⎠
⎝ 2
⎠
Obtém-se uma nova expressão E. O conjunto domínio, o conjunto-imagem e o período da função f(x) = E são,
respectivamente,
(A) {x ∈ IR ⏐ x ≠ kπ, k ∈ Z}, IR, π
(B) IR, [–1, 1], 2π
(C) {x ∈ IR ⏐ x ≠
π
+ kπ, k ∈ Z}, IR, π
2
(D) {x ∈ IR ⏐ x ≠ kπ, k ∈ Z}, [–1, 1], 2π.
(E) N.R.A.
5. Um pasto homogêneo tem a forma de um circulo. Um burro está preso por uma corda de comprimento igual ao raio do
círculo, amarrada a uma estaca na circunferência do círculo. A melhor aproximação da porcentagem da grama do pasto que
o burro consegue comer é:
(A) 45%
(B) 42%
(C) 39%
(D) 36%
(E) 32%.
6. Seja f: IR → IR \ {0} uma função satisfazendo às condições:
f(x + y) = f(x) f(y), para todo x, y ∈ IR e f(x) ≠ 1, para todo x ∈ IR \ {0}.
Das afirmações:
I. f pode ser ímpar.
II. f (0) =1.
III. f é injetiva.
IV. f não é sobrejetiva, pois f (x) > 0 para todo x ∈ IR.
é(são) falsa(s) apenas
(A) I e III.
(B) II e III.
(C) I e IV.
(D) IV.
(E) I.
7. Sejam as matrizes reais de ordem 2,
1 ⎤
⎡2 + a a ⎤
⎡1
A= ⎢
e B= ⎢
⎥
⎥
1⎦
⎣ 1
⎣a 2 + a ⎦
Então, a soma dos elementos da diagonal principal de (AB)-1 é igual a:
(A) a + 1
(B) 4(a + 1)
1
(C) (5 + 2a + a2)
4
1
(D) (1 + 2a + a2)
4
1
(E) (5 + 2a + a2).
2
8. Considere, no plano complexo, um hexágono regular centrado em z0 = i. Represente por z1, z2, ..., z6 seus vértices,
quando percorridos no sentido anti-horário. Se z1 = 1, então 2z3 é igual a:
(A) 2 + 4i.
(B) ( 3 -1) + ( 3 + 3)i.
6 + ( 2 + 2)i.
(C)
(D) (2 3 - 1) + (2 3 + 3)i.
2 + ( 6 + 2)i.
(E)
9. Quantas raízes reais têm a equação
x + 20 = x ?
(A) Nenhuma.
(B) Uma.
(C) Duas, as quais são positivas.
(D) Duas, as quais são negativas.
(E) Duas, as quais têm sinais opostos.
10. Se a, b, m e n são números reais tais que a 2 + b 2 = 341ab , a ≠ 0 , b ≠ 0 , log 3 2 = m e log 3 7 = n então o valor da
expressão
2
log 3
[a + b] 2
⎡7⎤
− log 3 ⎢ ⎥ − 2 [log 9 2] 2 + log 1 14 é:
64ab
⎣3⎦
3
(A) m 2 + 6n − 1 .
m2
− 7m + 2 .
2
n2
+ 3m − 6n − 2 .
(C) 3
2
n2
+ 6n − 1 .
(D)
2
(B) −
(E) − n 2 + 6m − 1 .
11. Considere no plano cartesiano xy o triângulo delimitado pelas retas 2x= y, x= 2y e x= – 2y + 10. A área desse triângulo
mede:
(A) 15
2
13
(B)
4
(C) 11
6
(D) 9
4
7
(E) .
2
12. No tetraedro ABCD, a face ABC é um triângulo equilátero de lado 4 e aresta AD, que mede 3, é perpendicular às
arestas AB e AC. A distância do vértice A à face BCD é:
(A) 4 3
(B) 6
6 7
(C)
7
6 3
(D)
5
2 21
.
(E)
21
13. Um triângulo ABC apresenta lados a, b e c. Sabendo que B̂ e Ĉ são, respectivamente, os ângulos opostos aos lado b e
c, o valor de
(A)
(B)
(C)
(D)
tg B̂
tg Ĉ
é
a 2 − b 2 + c 2c
a 2 + b2 − c2b
a 2 + b2 − c2
a 2 − b2 + c2
a 2 − b2 + c2
a 2 + b2 − c2
a 2 + b 2 − c 2c
a 2 − b 2 + c2b
b
(E)
c
14. Um octaedro regular está inscrito num cubo de aresta a. A razão entre o volume do cubo e o volume do octaedro é:
(A) 2.
(B) 3.
(C) 4.
(D) 5.
(E) 6.
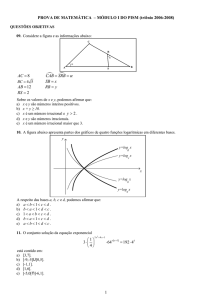
15. No gráfico abaixo estão representadas as funções reais f e g sendo A = f ∩ g
É FALSO afirmar sobre as mesmas funções que
(A) (fog)(x) ≥ 0 ⇒ g(x) ≥ –2
−1
(B) se s(x) =
, então o domínio de s é dado por IR *− –{–2}
100
101
[f ( x )] .[g( x )]
(C) o gráfico da função j definida por j(x) =
f −1 ( x )
possui pontos no 4º quadrante
g −1 ( x )
(D) se h: IR → B tal que h(x) = f(x) . g(x), então h será bijetora se B = [–2, +∞[
(E) N.R.A.
16. Considere o triângulo ABC de lados a = BC , b = AC e c = AB e ângulos internos α = CÂB, β = A B̂ C e γ = B Ĉ A.
Sabendo-se que a equação x2 − 2bx cosα + b2 − a2 = 0 admite c como raiz dupla, pode-se afirmar que
(A) α = 90º.
(B) β = 60º.
(C) γ = 90º.
(D) O triângulo é retângulo apenas se α = 45º.
(E) O triângulo é retângulo e b é hipotenusa.
17. Considere a função real f de variável real e as seguintes proposições:
I) Se f é contínua em um intervalo aberto contendo x = x0 e tem um máximo local em x = x0 então f’(x0) = 0 e f”(x0) < 0.
II) Se f é derivável em um interval aberto contendo x = x0 e f’(x0) = 0 então f tem um máximo ou um mínimo local em x =
x0.
III) Se f tem derivada estritamente positiva em todo o seu domínio então f é crescente em todo o seu domínio.
IV) Se
lim f(x) = 1 e lim g(x) é infinito então lim (f(x))g(x) = 1.
x→a
x→a
x→a
f (x) − f (x − 2s)
V) Se f e derivavel ∀x ∈ IR, então lim
= 2f’(x).
s→0
2s
Podemos afirmar que
(A) todas são falsas
(E) todas são verdadeiras
(C) apenas uma delas é verdadeira
(D) apenas duas delas são verdadeiras
(E) apenas uma delas é falsa
18. Considere a progressão aritmética (a1, a2, ..., a50) de razão d. Se
10
∑a
n =1
a
(A) 3
(B) 6
(C) 9
(D) 11
(E) 14
\
n
= 10 + 25d e
50
∑a
n =1
n
= 4550, então d – a1 é igual
19. Seja o conjunto S = {r ∈ Q : r ≥ 0 e r2 ≤ 2}, sobre o qual são feitas as seguintes afirmações:
5
7
I.
∈S e ∈S
4
5
II. {x ∈ IR : 0 ≤ x ≤
2 }∩S=∅
III. 2 ∈ S.
Pode-se dizer, então, que é (são) verdadeira(s) apenas
(A) I e II
(B) I e III
(C) II e III
(D) I
(E) II.
20. Uma tigela tem a forma de uma semi-esfera de raio 30cm 3 se encontra sobre uma mesa. Uma gota d’água se
encontra na borda da tigela e começa a escorrer externamente sobre ela com uma velocidade de 2,5π cm / s . Após 2
segundos, a distância entre a gota d’água e a mesa é de:
(A) 15 3 cm
(B) 15 cm
(C) 10 cm
(D) 15
(E)
3
cm
2
30
cm .
π
Gabarito
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
C
B
B
A
C
E
C
B
B
B
A
C
B
E
D
E
C
D
D
B