M H S Turma: M2S

Material Complementar
Professor Penha
Cada ida e volta do corpo (oscilação) é chamada ciclo, onde:
Período (T)  é o tempo de duração de um ciclo. No SI dado em segundos (s)
Freqüência (f)  é o número de ciclos que o corpo realiza na unidade de
tempo. No SI dada em hertz(Hz)
MOVIMENTO HARMÔNICO SIMPLES (M.H.S.)
Um corpo efetua um movimento harmônico simples (MHS) quando, numa
trajetória retilínea, oscila periodicamente em torno de uma posição de equilíbrio sob a
ação de uma força cuja intensidade é proporcional à distancia do ponto à posição de
equilíbrio. Essa força é sempre orientada para a posição de equilíbrio e chama-se força
restauradora.
Relação entre T e f:
f
ENERGIA NO M.H.S.
1
T
O período do sistema massa-mola é dado por:
Em oscilações mecânicas observamos seguidamente transformações
de energia cinética em energia potencial e vice-versa.
T  2
m
k
Podemos ver que no sistema massa mola o período:
- depende a massa oscilante.
- não depende da amplitude.
- não depende da aceleração gravitacional local, mesmo que a oscilação ocorra
na vertical ou num plano inclinado
A aceleração do sistema massa-mola é dada por:
a = -k x
m
RELAÇÃO ENTRE M.C.U E M.H.S.
O MHS e o movimento circular uniforme (MCU) estão
relacionados, de modo que um pode ser estudado através do outro.
Note que, enquanto a partícula descreve uma volta completa, sua
projeção realiza um movimento de vaivém sobre o eixo horizontal (MHS).
Portanto, a projeção horizontal do MCU realiza um MHS.
Comparando a Energia Cinética do bloco com a Energia Potencial Elástica da mola.
Funções do movimento
Considera-se o movimento a seguir, em que um ponto o descreve um
MCU, observa-se também a projeção (sombra) do ponto s na horizontal.
As equações seguintes nos permite obter a elongação (x), a velocidade
(v) e a aceleração (a) para s em qualquer instante (t).
- elongação:
O bloco e a mola da figura abaixo, constituem um conjunto denominado
oscilador harmônico.
Gráfico da elongação para fase inicial igual a zero (0 = 0)
O valor máximo da abscissa x é denominado amplitude A e corresponde às
posições extremas do bloco em que ocorreu a inversão de sentido do movimento.
O movimento do oscilador harmônico é um MHS, onde a força restauradora
é a força elástica dada por:
Fel = -kx
1
Material Complementar
Professor Penha
Onde:
x  elongação
v  velocidade da partícula em MHS
a  aceleração da partícula em MHS
A  amplitude
0  ângulo de fase inicial (t0 = 0)
  pulsação do MHS ou freqüência angular (velocidade angular no MCU)
t  instante do movimento
- velocidade
θ vo
t
vs
R=A
θ
-A
PÊNDULO SIMPLES
t=0
vs
0
Quando o pêndulo é deslocado de sua posição de equilíbrio e solto, ele
oscila sob a ação da força peso, apresentando um movimento periódico.
Chamamos de movimento harmônico, qualquer movimento que se repete a
intervalos regulares de tempo. As forças que atuam sobre a esfera de massa m
são: a força peso p e a força de tração T, que o fio exerce sobre a esfera em
qualquer instante.
Quando o ângulo  for muito pequeno (10º) podemos fazer a
aproximação de que sen  = . Neste caso, o pêndulo executa um movimento
harmônico simples(MHS).
x
A
v  A.sen ( 0  t )
Gráfico da velocidade para fase inicial igual a zero (0 = 0)
O período do pêndulo simples é dado pela expressão:
Aceleração
vo
a
T  2
t
Onde:
T= período (s);
L= comprimento do fio (m);
g= aceleração da gravidade (m/s2).
θ
R=A
a cp
-A
0
O período do pêndulo simples :
- não depende da massa oscilante.
- não depende da amplitude, desde que  < 150
- depende apenas da aceleração gravitacional local e do comprimento do fio
t=0
θ
a

g
A
x
EXERCÍCIOS
01.A energia mecânica associada a um sistema massa-mola que oscila
horizontalmente é 32J. A constante elástica da mola, de massa desprezível, é
400N/m. Nas afirmações abaixo marque (V) para verdadeira e (F) para falsa.
( ) A amplitude do movimento é 0,4m
( ) Nos extremos da trajetória a energia potencial é máxima.
( ) No ponto central da trajetória a energia cinética é máxima.
( ) Para uma elongação de 02 2 m, a energia potencial elástica tem o mesmo
valor que a energia cinética.
a   2 A. cos ( 0  t )
02.O período de oscilação de um sistema massa-mola é de πs. Se a massa do
corpo oscilante é de 1kg, qual será a constante elástica da mola do sistema?
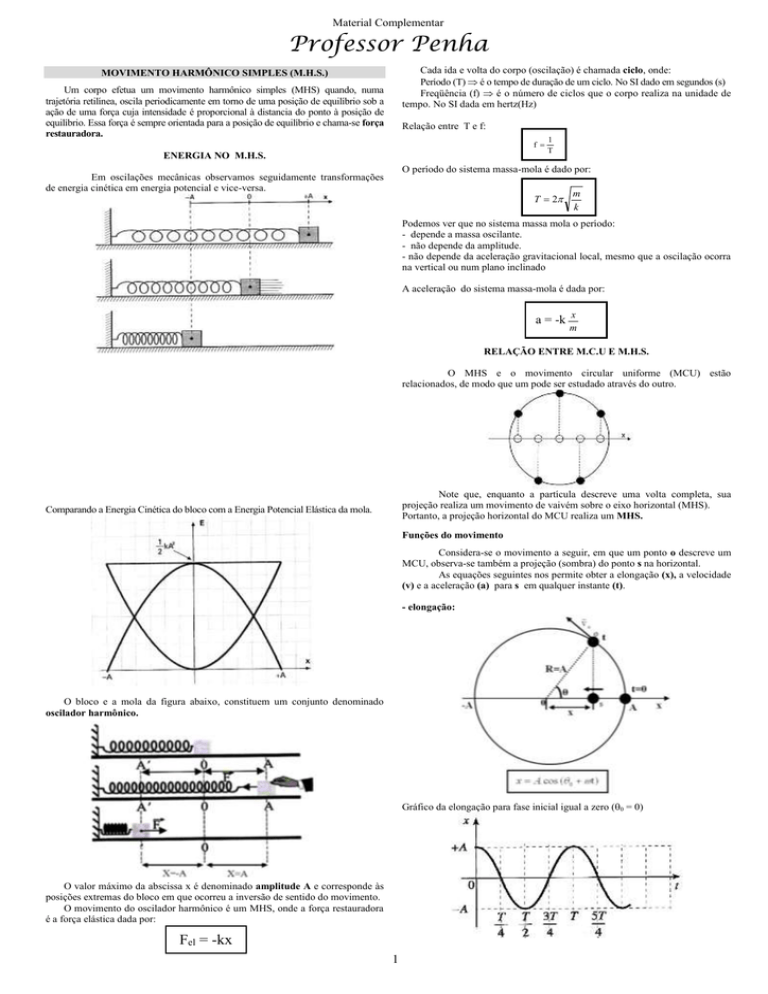
03.Um corpo executa oscilações harmônicas do ponto O com período de 4s. Os
pontos P e Q são os extremos da oscilação. No instante inicial o móvel está
passando pela posição central e movendo-se para a direita.
Gráfico da aceleração para fase inicial igual a zero (0=0)
Pra esse movimento, determine:
a) a freqüência, a pulsação, a amplitude e a fase inicial.
b)a equação horária dos espaços
c)as equações da velocidade e da aceleração.
d)a velocidade no instante inicial.
e) a elongação, velocidade e aceleração no instante t igual 6s
2
Material Complementar
Professor Penha
04.Um pêndulo simples está oscilando, e os atritos com o ar e no ponto de
fixação, reduzem gradualmente a amplitude de seu movimento. Afirma-se que:
I. A velocidade escalar máxima da pêndulo está diminuindo.
II. A aceleração escalar máxima do pêndulo está aumentando.
III. O período de oscilação e a amplitude diminuem na mesma proporção.
Analisando as afirmativas acima, deve-se concluir que:
A) somente I é correta.
B) somente II é correta.
C) somente III é correta.
D) somente I e II são correta.
E) somente I e III são correta.
A) quando o bloco passa pelos pontos extremos, isto é, em x = ± 0,1m, a
aceleração do bloco é nula nesses pontos.
B) o módulo da força que a mola exerce sobre o bloco na posição + 0,1m é
2,0.103N.
C) a constante elástica da mola vale 2,0.10 4 N/m.
D) a energia potencial do bloco na posição + 0,05m vale 100J.
E) na posição de equilíbrio, o módulo da velocidade do bloco é 20m/s.
10.(UFPB) Um corpo, preso a uma mola ideal de constante elástica k , realiza
um movimento harmônico simples, oscilando em torno da posição de equilíbrio
x = 0. O gráfico ao lado mostra sua energia cinética Ec , em função de sua
posição x . Determine, em N/m, o valor da constante elástica k.
05.(UFV) Uma partícula presa a uma mola executa um movimento harmônico
simples. É CORRETO afirmar que o módulo da velocidade da partícula é:
a) máximo quando a elongação é máxima.
b) mantido constante.
c) máximo quando ela apresenta a aceleração máxima.
d) mínimo quando a elongação é mínima.
e) mínimo quando ela apresenta a aceleração máxima.
06.(ACAFE) O gráfico abaixo mostra a elongação em função do tempo para um
movimento harmônico simples. A alternativa que contém a equação horária da
posição deste movimento é:
11.(UEMf1) A função horária da posição de uma partícula que realiza um
Movimento Harmônico Simples (MHS) é x  A cos(t  ) . A figura a
seguir apresenta o gráfico da função horária da posição de uma partícula que
descreve um MHS segundo um certo referencial.
A) x = 4 cos [(3/2) t + ]
C) x = 2 cos  t
E) x = 2 cos (t + /2)
B) x = 4 cos [(/2) t + 3/2]
D) x = 2 cos [(/2) t + ]
07.(UEM) Duas molas idênticas de constante elástica K são conectadas em
paralelo (figura 1) e em série (figura 2) a um bloco de massa M. Qual a razão
entre o período de oscilação das molas conectadas em paralelo e o período de
oscilação das molas conectadas em série?
k
k
M
A) 2
A) 2

M
B) 4
*C) 1/2
B) 4
C) 1/2
D) 1
D) 1

A) x  0,10cos( t  )m.
2
2

3
C) x  0,10sen( t 
)m.
2
2

3
E) x  0,10cos( t 
)m.
2
2
k
M
k
A função horária da posição dessa partícula com dados no Sistema
Internacional (SI) de unidades é
E) 3/4
E) 3/4
08.Quando um ponto material percorre, em um movimento circular uniforme,
uma circunferência, a projeção deste ponto material sobre um diâmetro da
circunferência realiza um movimento harmônico simples (MHS). Sobre esse
movimento, assinale (V) ou (F)
( ) Em determinado momento, a velocidade e a elongação do ponto material em
MHS podem ser simultaneamente nulas.
( ) Nos pontos de inversão, a aceleração do MHS é máxima.em módulo.
( ) Nos pontos de inversão do MHS, a velocidade do ponto material é máxima.
( ) Em determinado momento, a velocidade e a aceleração do ponto material em
MHS podem ser simultaneamente nulas.
( ) Excluindo os pontos em que a elongação é máxima, os demais pontos da
elongação apresentam velocidades iguais, porém, opostas.


B) x  0,20cos( t  )m.
2
2

D) x  0,20cos( t )m.
2
12.(UEM) Suponha que um pequeno corpo, de massa m, esteja preso na
extremidade de um fio de peso desprezível, cujo comprimento é L, oscilando
com pequena amplitude, em um plano vertical, como mostra a figura a seguir.
Esse dispositivo constitui um pêndulo simples que executa um movimento
harmônico simples. Verifica-se que o corpo, saindo de B, desloca-se até B' e
retorna a B, 20 vezes em 10 s. Sobre esse movimento assinale (V) ou (F).
09.Um bloco de massa m = 1 kg preso à extremidade de uma mola e apoiado sobre uma
superfície horizontal sem atrito, oscila em torno da posição de equilíbrio, com uma
amplitude de 0,1 m, conforme mostra a figura (a) abaixo. A figura (b) mostra como a
energia cinética do bloco varia de acordo com seu deslocamento.
( ) O período deste pêndulo é 2,0 s.
( ) A freqüência de oscilação do pêndulo é 0,5 Hz.
( ) Se o comprimento do fio L for 4 vezes maior, o período do pêndulo será
dobrado.
(
) Se a massa do corpo suspenso for triplicada, sua freqüência ficará
multiplicada por 3 .
( ) Se o valor local de g for 4 vezes maior, a freqüência do pêndulo será duas
vezes menor.
(
) Se a amplitude do pêndulo for reduzida à metade, seu período não
modificará
13.(UEM)O peso de um objeto na Lua é 1/6 de seu peso na Terra. Um relógio
de pêndulo que oscila com um período de 1s na Terra oscilará, sobre a Lua,
com um período de
É CORRETO afirmar que:
3
A) (1 / 6 ) s.
B) 1,6 s.
D) 1,0 s.
E)
6 s
C) 6,0 s.
Material Complementar
Professor Penha
14.(MACKENZIE) Um corpo de 50 g, preso à extremidade de uma mola ideal
(constante elástica = 3,2 N/m) comprimida de 30 cm, é abandonado do repouso
da posição A da figura. A partir desse instante, o corpo inicia um movimento
harmônico simples. Despreze os atritos e adote o eixo x com origem no ponto de
equilíbrio do corpo (ponto O) e sentido para a direita. A função que mostra a
velocidade desse corpo em função do tempo, no Sistema Internacional, é:
A) v = - 2,4 sen (8.t + )
C) v = - 7,2 sen (4.t + ).
E) v = - 1,2 sen (2.t + ).
(02) O gráfico abaixo representa a velocidade v do ponto material em função
do tempo t.
(04) A força restauradora que atua sobre o ponto material é inversamente
proporcional à amplitude do movimento.
08) O gráfico do período T de oscilação em função da massa m do ponto
material é bem representado pelo gráfico abaixo.
B) v = - 0,03 sen (3,2.t + ).
D) v = - 2,7 sen (4.t + ).
15.(UEM) Imagine um poço que perfure toda a Terra, atravessando-a de uma
extremidade a outra. Desconsidere o calor do interior terrestre, os efeitos nãoinerciais da rotação terrestre e despreze totalmente a resistência do ar no interior
do poço. Responda os seguintes itens:
A) que tipo de movimento fará uma bola de massa m ao ser deixada cair no
interior do poço? (Considere a densidade da Terra constante em qualquer ponto
da trajetória de queda da bola; considere ainda a densidade ρ da Terra dada
por ρ = M / [(4/3) π R3], em que M é a massa da Terra e R o raio de nosso
planeta; considere, em primeira aproximação, que a distância que separa o centro
da bola e o centro da Terra é igual ao raio da Terra).
B) justifique fisicamente a resposta, ou seja, demonstrando-a através do uso da
formulação gravitacional de Newton e da noção de densidade.
(16) A força restauradora, que atua sobre o ponto material, em relação ao
deslocamento do mesmo, é representada por uma função linear.
19.(UFG)Uma mola de constante elástica k = 50 N/m e massa desprezível tem
uma extremidade fixa no teto e a outra presa a um corpo de massa m=0,2kg. O
corpo é mantido inicialmente numa posição em que a mola está relaxada e na
vertical. Ao ser abandonado, ele passa a realizar um movimento harmônico
simples, em que a amplitude e a energia cinética máxima são, respectivamente,
Dado: g = 10 m/s2
A) 4 cm e 0,04 J
B) 4 cm e 0,08 J
C) 8 cm e 0,04 J
D) 8 cm e 0,08 J
E) 8 cm e 0,16 J
16.(Unifesp)Um estudante faz o estudo experimental de um movimento
harmônico simples (MHS) com um cronômetro e um pêndulo simples como o da
figura, adotando o referencial nela representado.
20.(UEM-2009cg)Considerando
a
função
posição
x(t) = 2cos(0,4πt + π/6), com x dado em centímetros e t em segundos, de um
corpo em movimento harmônico simples, assinale o que for correto.
01) Nas mesmas unidades acima, podemos também expressar x(t) na forma
√3cos (0,4 πt)sen (0,4πt) , em que t ≥ 0 .
02) O período do movimento é 2πsegundos.
04)
O
primeiro
instante
t
em
que
x(t)
2
cm
é
t = 55/12segundos.
08) A amplitude do movimento é 2 cm.
16) No intervalo de tempo 0,6, o corpo passa somente
duas vezes pela posição em que x(t) 0 .
Ele desloca o pêndulo para a posição +A e o abandona quando cronometra o
instante t = 0. Na vigésima passagem do pêndulo por essa posição, o cronômetro
marca t = 30 s.
a) Determine o período (T) e a freqüência (f) do movimento desse pêndulo.
b) Esboce o gráfico x (posição) × t (tempo) desse movimento, dos instantes t = 0
a t = 3,0 s; considere desprezível a influência de forças resistivas.
GABARITO:
01) VVVV
02)4N/m
03)a) f =1/4Hz, /2rad/s, 2m, 0=3/2rad
 3  
 t
 2 2 
b) s=2.cos 
17.(UFC)Uma partícula, de massa m, movendo-se num plano horizontal, sem atrito,
é presa a um sistema de molas de quatro maneiras distintas, mostradas a seguir.
 3  
 
 t  ou v = .cos  t 
2
2


2 
c) v = -.sen 
a=
2
2
2
 3  
 
 t  ou a = .sen  t 
2
2
2


2 
.cos 
d) v0 = m/s
e) x = 0
Com relação às freqüências de oscilação da partícula, assinale a alternativa correta.
A) As freqüências nos casos II e IV são iguais.
B) As freqüências nos casos III e IV são iguais.
C) A maior freqüência acontece no caso II.
D) A maior freqüência acontece no caso I.
E) A menor freqüência acontece no caso IV.
v = -m/s
a=0
04) a
05) e
06) d
07) c
08) fvffv
09) e
10)48
11) e
12)ffvffv 13) e
14) a
15) a) M.H.S.
b) F = kr
16) a) T = 1,5 s; f = 0,67 Hz
b) Observando-se que em t = 0, x = + A, temos o gráfico senoidal a seguir.
18.(UEM–2009) Considere um ponto material de massa m que oscila em torno
de uma posição de equilíbrio, em trajetória retilínea, livre de forças dissipativas.
Assinale a(s) alternativa(s) correta(s).
(01) A função x = f (t) , na qual x é o deslocamento do ponto material e t é o
tempo, é bem representada pelo gráfico abaixo.
17)b
18) 25
19) a
20)13
4