um estudo sobre logaritmos e o uso de calculadora científica e da

0
KELEN PEREIRA LIMA DA SILVA
UM ESTUDO SOBRE LOGARITMOS E O USO DE CALCULADORA
CIENTÍFICA E DA HISTÓRIA DA MATEMÁTICA
Assis
2011
KELEN PEREIRA LIMA DA SILVA
UM ESTUDO SOBRE LOGARITMOS E O USO DE CALCULADORA
CIENTÍFICA E DA HISTÓRIA DA MATEMÁTICA
Trabalho
de
conclusão
de
curso
a
ser
apresentado para defesa ao Instituto Municipal
de Ensino Superior de Assis, como requisito do
Curso de Licenciatura em Matemática.
Orientadora: Sarah Rabelo de Souza
Área de Concentração: Ciências Sociais e Aplicadas
Assis
2011
FICHA CATALOGRÁFICA
SILVA, Kelen Pereira Lima da
Um estudo sobre logaritmos e o uso de calculadora científica e da História da
Matemática. / Kelen Pereira Lima da Silva . Fundação Educacional do Município de Assis –
Assis, 2011.
36 p.
Orientadora: Sarah Rabelo de Souza
Trabalho de Conclusão de Curso – Instituto Municipal de Ensino Superior de Assis
1. Logaritmos. 2. Calculadora. 3.História da Matemática.
KELEN PEREIRA LIMA DA SILVA
UM ESTUDO SOBRE LOGARITMOS E O USO DE CALCULADORA
CIENTÍFICA E DA HISTÓRIA DA MATEMÁTICA
Trabalho
de
conclusão
de
curso
a
ser
apresentado para defesa ao Instituto Municipal
de Ensino Superior de Assis, como requisito do
Curso de Licenciatura em Matemática, analisado
pela seguinte comissão examinadora:
Orientadora: Sarah Rabelo de Souza______________________________________
Analisadora: Maria Beatriz Alonso do Nascimento____________________________
Assis
2011
DEDICATÓRIA
Dedico este trabalho de conclusão de curso aos meus pais,
Antônio José e Ortência, que tanto me incentivaram para que eu
continuasse meus estudos. É dedicada, também, a minha
orientadora Sarah Rabelo uma pessoa maravilhosa e muito gentil
e ao meu professor Claudio que me incentivou a fazer este curso.
AGRADECIMENTOS
Á Orientadora Professora SARAH RABELO DE SOUZA pela orientação, dedicação e
paciência.
A Professora MARIA BEATRIZ ALONSO DO NASCIMENTO por aceitar examinar meu
trabalho.
Á Profª. Ms. Leonor Farcic Fic Menk coordenadora do curso que sempre incentivo os
alunos.
Aos professores que contribuíram para a minha formação.
Aos colegas e amigos que de forma direta ou indireta participaram desta
etapa de aprendizado tão importante na minha vida.
Ao meu pai Antônio José da Silva e minha mãe Ortência de Jesus Lima por me
apoiarem e confiarem em mim.
À minha irmã Suelen e meu irmão Matheus, sempre presentes na minha vida.
A Deus por me dar forças.
Obrigada do fundo do meu coração, sem todos vocês seria difícil concluir este trabalho.
RESUMO
Esse trabalho teve como objetivo trabalhar logaritmos utilizando a História da Matemática e o
uso de calculadoras científicas. O conceito de logaritmos muitas vezes é visto com
dificuldade entre os alunos do Ensino Médio e a utilização destes recursos pode auxiliar no
ensino deste conteúdo. Neste trabalho, foi realizada uma pesquisa com um grupo de
alunos de uma escola estadual de uma cidade do interior paulista. Após a realização de préteste acerca dos conhecimentos dos alunos sobre os logaritmos e sua história, foi realizada
uma oficina mostrando a história, as aplicações de logaritmo na matemática financeira e o uso
da calculadora científica. Foi realizado um pós-teste cujo resultado mostrou um aprendizado
deste conteúdo. Os alunos mostraram-se satisfeitos com a abordagem utilizada para aprender
logaritmos.
Palavras-chave: 1. Logaritmos. 2. Calculadora. 3.História da Matemática
ABSTRACT
This work was aimed at work using logarithms to the history of mathematics and the use of
scientific calculators. The concept of logarithms is often seen with difficulty among middle school
students and the use of these resources can assist in the teaching of this content. This work was
carried out a search with a group of students from a State school, a city of São Paulo. After the
completion of students ' knowledge about pre-test on logarithms and its history, was held a
workshop showing the history, applications of logarithm in financial mathematics and the use of
scientific calculator. It was held a post-test whose result showed an apprenticeship of this
content. Students were satisfied with the approach used to learn logarithms.
Keywords : 1. Logarithms. 2. Calculator. 3 Mathematics History
SUMÁRIO
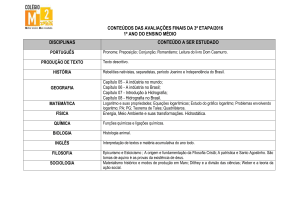
1. INTRODUÇÃO ......................................................................... .......09
2. O QUE É LOGARITMO.....................................................................11
2.1.
O LOGARITMO E SEUS USOS ...................................................................11
3. HISTÓRIA DO LOGARITMO ................................................... .......15
4. APLICAÇÕES DO LOGARITMO ............................................. .......20
5. A IMPORTÂNCIA DA CALCULADORA CIENTÍFICA NO ENSINO DO
LOGARITMO ................................................................................ .....25
6. A IMPORTÂNCIA DA HISTÓRIA DA MATEMÁTICA NO ENSINO E
APRENDIZAGEM ................................................................... ..........26
7. A PESQUISA ............................................................................ .....27
7.1.
ANÁLISE DOS RESULTADOS ...................................................................28
8. CONSIDERAÇÕES FINAIS ...................................................... ....33
9. REFERÊNCIAS ......................................................................... ....34
9
1. INTRODUÇÃO
Esse trabalho consiste em realizar um estudo histórico sobre logaritmos e suas
aplicações. O conceito de logaritmos muitas vezes é visto com dificuldade entre os
alunos do Ensino Médio.
Neste trabalho, foi realizada uma pesquisa com um grupo de alunos de uma escola
estadual da cidade de Assis, São Paulo, acerca dos conhecimentos sobre logaritmos,
sua história e uso da calculadora científica. Foi realizada uma oficina com esses alunos
sobre a história dos logaritmos, conceitos, aplicações, e uso da calculadora científica e
verificada, por meio de entrevista coletiva, a opinião destes acerca das informações
trabalhadas.
A metodologia utilizada foi estudo de caso, considerando uma pesquisa qualitativa.
Os logaritmos constituem um tema muito importante em nosso estudo, com muitas
aplicações na Matemática e em outras áreas do conhecimento.
O objetivo geral deste trabalho é apresentar o conceito de logaritmo a um grupo de
alunos do 3º ano do Ensino Médio de uma escola estadual, de maneira a abordar sua
história, aplicações e o uso da calculadora científica.
Como objetivos específicos, temos: realização de uma apresentação sobre a revisão
histórica dos logaritmos onde foi verificado o conhecimento dos alunos acerca do
conceito de logaritmo verificamos também o conhecimento dos alunos sobre o uso da
calculadora científica, no que se refere aos logaritmos e a opinião dos alunos sobre
logaritmos após o desenvolvimento de uma atividade planejada e realizada.
Esse trabalho pode contribuir para facilitar a compreensão de um grupo de alunos do
Ensino Médio sobre logaritmo e o uso da calculadora científica no que se refere a esse
conteúdo. Para isso foi realizada uma oficina que tratou do estudo do logaritmo e do
10
uso da calculadora científica, o que pode tornar mais agradável a apreensão desse
conceito.
Os alunos que participaram da oficina realizada puderam ter uma revisão do conceito
de logaritmo, conhecer sua história, além de terem a oportunidade de utilizar a
calculadora científica.
11
2. O QUE É LOGARITMO
Logaritmo é o processo matemático que tem como finalidade encontrar qual deve
elevar um número escolhido como base para obter o valor de um número pelo qual
deseja fazer esta representação (FACCHINI,1996).
A ideia de logaritmo é muito simples, e pode-se dizer que o nome logaritmo é uma nova
denominação para expoente. Procurar um expoente trata-se de achar o logaritmo.
2.1 O LOGARITMO E SEUS USOS
A idéia dos logaritmos é de transformar operações aritméticas complicadas, como
potenciação e radiciação, em operações mais simples. Antes de falarmos desse
alcance dos logaritmos, vamos compreender melhor seu significado.
Dados dois números reais positivos, a e b, com a  1 , existe um único número real x de
modo que ax = b.
Este número x é chamado de logaritmo de b na base a e indica-se loga b.
ax = b <=> x = loga b ( 1  a > 0, b > 0)
Note que logaritmo de b na base a nada mais é que o expoente ao qual se deve elevar
o número a para obter b.
12
Na igualdade x = loga b, temos;
a = base do logaritmo;
b = logaritmando ou antilogaritmo;
x = logaritmo.
Exemplos:
1) log2 32 = 5 pois 25 = 32
2) log4 16 = 2, pois 42 = 16
3) log8 8 = 1, pois 81 = 8
4) log3 81 = 4, pois 34 = 81
5) log5 1 = 0, pois 50 = 1
Observações:
1) A base deve ser positiva e diferente de 1, pois 1 x = 1, qualquer X  R, e 0x (X(a  R)
13
e ax (a < 0 e X  R) nem sempre são definidos.
2) Os números negativos e o zero não tem logaritmo. Já vimos que loga b = x <=> ax = b
e sabemos que ax é positivo (potência de base positiva é positiva). Portanto, b é
positivo.
3) Quando escrevemos somente log b sem indicar a base, está subentendido que a
base é 10. Assim, log b = log10 b. Por exemplo: Log 100 = 2
Quando não tiver a base significa que a base é 10, e é chamado de logaritmo decimal.
Toda vez que a base for 10 e cair em uma potência, como 100, 1000, 10.000000, 0.001
é só contar quantos zeros tem a direita do um.
ex: log 100 = 2
ex: 1000 = 3
ex: 10000 = 4
E quando o 0 estiver a esquerda do um o resultado será negativo.
ex: log 0, 001 = -3
14
ex: log 0, 0001 = -4
ex: log 0, 00001 = -5
Propriedade da mudança de base
Existem situações nas quais precisaremos utilizar a tábua de logaritmos ou uma
calculadora científica na determinação do logaritmo de um número. Mas para isso
devemos trabalhar o problema no intuito de estabelecer o logaritmo na base 10, pois as
tábuas e as calculadoras operam nessas condições, para isso utilizamos a propriedade
da mudança de base, que consiste na seguinte definição:
Exemplo:
Em vários cálculos de logaritmos ou operações envolvendo logaritmos é preciso
transformar a base do logaritmo em outra, para facilitar as operações.
15
3. HISTÓRIA DO LOGARITMO
No final do século XVI, um dos desafios da Matemática era de encontrar um modo para
simplificar os cálculos aritméticos. Sendo assim no século XVII foi criado o logaritmo
para facilitar nos cálculos, onde as grandes navegações, comércios, empréstimos de
dinheiros, da astronomia, entre outros setores do conhecimento exigiam cálculos muito
complicados, portanto, havia uma necessidade na época para que esses cansativos
cálculos fossem simplificados (BOYER,1974).
Um astrônomo, por exemplo, podia saber quais eram os cálculos que tinham de fazer,
mas às vezes, levava meses para obter o resultado.
Assim quando surgiram os logaritmos, um grande astrônomo da época, um austríaco
chamado Jahannes Kepler (1571-1630), saudou os logaritmos com muito entusiasmo,
afirmando que reduziam consideravelmente o tempo que ele tinha de dispensar aos
cálculos (EVES,1995).
A essência era substituir complicados cálculos de multiplicação e divisão, por
operações mais simples como a soma e a subtração.
O conceito de logaritmo foi introduzido pelo matemático escocês John Napier (15501617) e aperfeiçoado pelo inglês, Henry Briggs (1561-1630) um dos precursores mais
importante (BOYER,1974).
Henry Briggs foi um matemático inglês, nasceu em 1561, e morreu em 1630, foi o
homem mais responsável pela aceitação dos LOGARITMOS pelos cientistas. Briggs foi
educado na Universidade de Cambridge, sendo o primeiro professor de geometria na
Faculdade de Gresham, Londres.
Em 1619, foi designado professor de geometria em Oxford. Briggs publicou trabalhos
16
em navegação, astronomia, e matemática. Propôs os logaritmos, com base dez, e
construiu uma tabela de logaritmos que foi usada até o século 19.
John Napier foi um dos que impulsionaram fortemente o desenvolvimento de logaritmo.
Ele é considerado o inventor dos logaritmos, muito embora outros matemáticos da
época também tenham trabalhado com ele (BOYER,1974).
Napier criou o termo logaritmo, por parecer com o termo logos arithmos, que significam,
respectivamente, "razão" e "número".
O escocês John Napier, além de administrar suas grandes propriedades, dedicava-se a
escrever sobre vários assuntos como, em 1593 lançou um livro dizendo poder provar
que o papa era o anticristo e que o Criador tencionava pôr fim ao mundo nos anos entre
1688 e 1700, ele era fervorosamente anticatólico, sendo convicto em suas opiniões.
Escrevia como um autêntico cientista, que foi o caso da criação dos logaritmos que
trabalhou por cerca de 20 anos na sua descoberta. E m 1614, Napier publicou o
resultado de parte das suas investigações, num primeiro livro, intitulado "Mirifi
Logarithmorum Canonis descriptio", (Uma Descrição do Maravilhoso Cânon de
Logaritmos) sem, contudo expor os meios que tinha empregado. Neste livro explica o
logaritmo natural comparando os termos da progressão aritmética e geométrica. Napier
esperou que, por meio dos seus logaritmos, ele salvaria os astrônomos por muito tempo
e os livraria dos erros de cálculos. Suas tabelas de logaritmos de funções
trigonométricas foram usadas durante quase um século (STRUIK, 1992).
Napier apresentou outro método de simplificar cálculos no seu Rabdologiae (1617).
Nesse ele descreveu um método de multiplicação que usa barras com números
marcados nelas. As barras de Napier foram feitas de marfim, então elas pareciam
ossos, e conduziram ao nome de ossos de Napier (Napier's bones) (BAUMGART,
1992). Multiplicação eram feitas colocando os ossos apropriados lado a lado, e lendo os
produtos apropriados. Essencialmente este dispositivo era uma tabela de multiplicar
com partes móveis. Napier também fez contribuições à trigonometria esférica, achou
17
expressões exponenciais para funções trigonométricas, e foi influente na introdução da
notação decimal para frações.
Já antes dos logaritmos, a simplificação das operações era realizada através das
conhecidas relações trigonométricas, que relacionavam produtos com somas ou
subtrações. Esse processo de simplificação das operações envolvidas passou a ser
conhecido como prostaférese, sendo largamente utilizado numa época em que as
questões relativas à navegação e à astronomia estavam no centro das atenções. De
fato, efetuar multiplicações ou divisões entre números muito grandes era um processo
bastante dispendioso em termos de tempo. A simplificação, provocada pela
prostaférese, era relativa e, sendo assim, o problema ainda permanecia (LIMA,1980).
O método de Napier baseou-se no fato de que associando aos termos de uma
progressão geométrica
b, b2, b3, b4, b5, … , bn, …
os termos da progressão aritmética
1, 2, 3, 4, 5, ... , n, ...
então ao produto de dois termos da primeira progressão, bm.bp, está associada a soma
m+p dos termos correspondentes na segunda progressão.
Considerando, por exemplo,
PA 1 2 3 4 5 6 7 8 9 10 11 12 13 14
PG 2 4
8 16 32 64 128 256 512 1024 2048 4096 8192 16394
Para efetuar, por exemplo, 256 x 32, basta observar que:
256 na segunda linha corresponde a 8 na primeira;
32 na segunda linha corresponde a 5 na primeira;
como 8+5=13,
13 na primeira linha corresponde a 8192 na segunda.
18
Assim, 256x32=8192 resultado esse que foi encontrado através de uma simples
operação de adição.
A fim de que os números da progressão geométrica estivessem bem próximos, para
ser possível usar interpolação e preencher as lacunas entre os termos na
correspondência estabelecida, evitando erros muito grosseiros, Napier escolheu para
razão o número = 0, 9999999, que é bem próximo de 1.
Enquanto Napier trabalhava com uma progressão geométrica onde o primeiro termo era
107.b e a razão b, ao que parece de forma independente, Bürgi também lidava com o
problema dos logaritmos.
Bürgi empregou uma razão um pouco maior do que 1, qual seja 1, 0001=1+10-4. O
primeiro termo de sua PG era 108 e ele desenvolveu uma tabela com 23027 termos.
Como Napier, Bürgi considerou uma PG cuja razão era muito próxima de 1, a fim de
que os termos da sequência fossem muito próximos e os cálculos pudessem ser
realizados com boas aproximações.
Posteriormente, Napier, juntamente com Briggs, elaboraram tábuas de logaritmos mais
úteis de modo que o logaritmo de 1 fosse 0 e o logaritmo de 10 fosse uma potência
conveniente de 10, nascendo assim os logaritmos briggsianos ou comuns, ou seja, os
logaritmos dos dias de hoje.
Hoje, porém, com o advento das espantosas e cada vez mais baratas e rápidas
calculadoras, ninguém mais em sã consciência usa uma tábua de logaritmos ou uma
régua de cálculo para fins computacionais. O ensino dos logaritmos, como um
instrumento de cálculo, está desaparecendo das escolas, os famosos construtores de
réguas de cálculo de precisão estão desativando sua produção e célebres manuais de
tábuas matemáticas estudam a possibilidade de abandonar as tábuas de logaritmos
(SOUZA,1996). Os produtos da grande invenção de Napier tornaram-se peças de
museu.
A função logarítmica, porém, nunca morrerá pela simples razão de que as variações
exponenciais
e
logarítmicas
são
partes
vitais
da
natureza
e
da
análise.
19
Conseqüentemente, um estudo das propriedades da função logarítmica e de sua
inversa, a função exponencial, permanecerá sempre uma parte importante do ensino da
matemática (BOYER, 1974)
20
4. APLICAÇÕES DO LOGARITMO
Os logaritmos possuem inúmeras aplicações no cotidiano, na matemática financeira,
Física e a Química utilizam as funções logarítmicas nos fenômenos em que os números
adquirem valores muito grandes, tornando-os menores, facilitando os cálculos e a
construção de gráficos.
Na Química, por exemplo, é utilizada quando se quer a acidez de uma solução que é
definida por uma grandeza chamada pH (abreviatura de potêncial hidrogeniônico), que
é o simétrico do logaritmo de [H+].
Em símbolos:
pH = - log [H+]
Exemplos
de
aplicações
logaritmos.htm):
Exemplo 1
Uma curiosidade da Química:
logb (x.y) = logb x + logb y
(http://www.brasilescola.com/matematica/aplicacoes-dos-
21
Em uma solução de 1 litro, encontramos 0,01 mol de íons hidrogênio. Esta solução é
ácida, básica ou neutra?
A concentração de íons hidrogênio é de 0,01 mol/l, ou seja, [H] =
logb (x/y) = logb x - logb y
Assim, concluímos que logb xa = a. logb x. Trata-se, portanto, de uma solução ácida,
pois o pH<7.
Exemplo 2
Paulo aplicou R$ 800,00 num investimento que rende 3% ao mês, a juros compostos.
Quanto tempo após a aplicação o saldo será de R$ 1.200,00?
22
Exemplo 3
Em uma determinada cidade a taxa de crescimento populacional e de 4% ao ano,
aproximadamente. Em quantos anos a população desta cidade irá dobrar, se a taxa de
crescimento continuar a mesma?
População do ano-base = P0
População após um ano = P0 (1,04) = P1
População após dois anos = P0 (1,04)² = P2
23
População após x anos = P0 (1,04)x = Px
Vamos supor que a população dobrará em relação ao ano-base após x anos, temos:
Exemplo 4
Em quanto tempo 800 g de certa substância radioativa, que se desintegra a uma taxa
de 2% ao ano, se reduzirá a 200 g? Use:
em que Q é a massa da substância, r é a taxa e t é o tempo em anos.
24
Tais exemplos foram utilizados para provar o uso dos logaritmos em várias ciências.
25
5.
A IMPORTÂNCIA DA CALCULADORA CIENTÍFICA NO ENSINO DO
LOGARITMO
A Calculadora Científica é uma grande facilitadora, pois nos permite montar expressões
matemáticas facilmente e obter resultados precisos.
A Calculadora abrange Juros Simples, Juros Compostos, Raiz Cúbica, Fatorial,
Permutação, Combinação, Arranjos, Seno, Cosseno, Tangente, Cotangente, Secante,
Cossecante, Exponencial, Logaritmo, Raiz Quadrada, PI, Porcentagem e Operações
Básicas: adição (soma), subtração (diferença), multiplicação (produto), divisão
(quociente).
26
6. A IMPORTÂNCIA DA HISTÓRIA DA MATEMÁTICA NO ENSINO E
APRENDIZAGEM
A história da Matemática é um valioso recurso para o processo de ensino e
aprendizagem da Matemática.
Através dessa ferramenta, o professor tem a possibilidade de desenvolver atitudes e
valores positivos frente ao conhecimento matemático. O aluno reconhecerá a
Matemática como uma criação humana, que surgiu a partir da busca de soluções para
resolver problemas do cotidiano, conhecerá as preocupações dos vários povos em
diferentes momentos históricos, identificando a utilização da Matemática em cada um
deles e estabelecerá comparações entre os conceitos e processos matemáticos do
passado e do presente. O contato com alguns fatos do passado pode ser uma dinâmica
bastante interessante para introduzir um determinado tema em sala de aula. Para
mostrar a importância da história da Matemática como uma dinâmica de se trabalhar os
conceitos matemáticos, citamos uma reflexão de D’Ambrósio (2001, p. 97):
As práticas educativas se fundam na cultura, em estilos de
aprendizagem e nas tradições, e a história compreende o registro
desses fundamentos. Portanto, é praticamente impossível discutir
educação sem recorrer a esses e a interpretações dos mesmos. Isso é
igualmente verdade ao se fazer o ensino das várias disciplinas. Em
especial da Matemática, cujas raízes se confundem com a história da
humanidade.
27
7. A PESQUISA
Essa é uma pesquisa qualitativa, abordando um estudo de caso com alunos do 3º ano
do Ensino Médio de uma Escola Estadual da cidade de Assis, SP, sobre logaritmos.
Foram aplicados questionários com perguntas objetivas e dissertativas a fim de verificar
o conhecimento dos alunos sobre logaritmos, sua história e o uso de calculadora
científica.
Foi aplicada uma oficina sobre esse tema e depois, os alunos forma questionados
novamente sobre este assunto e sobre a opinião deles em relação ao que aprenderam.
Foi realizada uma pesquisa bibliográfica, realizada por meio de livros, apostilas
disponibilizadas para a Rede Estadual de Ensino do Estado de São Paulo, revistas e
material disponibilizado pela internet.
A pesquisa foi realizada com 15 alunos, sendo 9 do sexo feminino e 6 do sexo
masculino.
Foi disponibilizada a calculadora científica, porém a maioria afirmou não saber usá-la e
não se lembravam do conteúdo.
Receberam a informação que após o pré-teste teriam a possibilidade de participar de
uma oficina para rememorar o conteúdo. Utilizaram cerca de 15 minutos para resolver
as questões do pré-teste.
Durante a oficina estiveram atentos. Ficaram satisfeitos em conhecer a História do
logaritmo e demonstraram entusiasmo ao utilizarem a calculadora científica.
A oficina teve duração de 50 minutos, com o uso do PowerPoint.
Dias depois foi aplicado o pós-teste (40 minutos), puderam usar a calculadora com
facilidade, sempre respeitando as limitações de cada um.
28
7.1. ANÁLISE DOS RESULTADOS
Fazendo uma comparação do primeiro teste com o segundo ouve uma melhora muito
boa de todos os alunos em geral.
Pré-teste
1. Você já usou a calculadora científica?
( )SIM
( )NÃO
R: 9 alunos responderam que sim e 6 que não
2. Você já estudou Logaritmo?
( ) SIM
( ) NÃO
R: 14 alunos responderam que sim, apenas uma respondeu que não
3. Se você já estudou logaritmo na escola, você achou:
( ) muito difícil
29
( ) difícil
( ) nem difícil nem fácil
( ) fácil
( ) muito fácil
R: 7 alunos responderam nem difícil nem fácil, 7 responderam difícil e apenas 1 aluno
respondeu muito difícil.
4. Você já usou calculadora científica para resolver problemas com logaritmo?
( ) SIM
( ) NÃO
R: todos responderam que não.
5. Resolva:
a)Log2 2
30
b)Log3 9
c)Log 100
d)Log5 25
R: questão a 9 acertos e 6 erros, b 5 acertos e 10 erros, c 5 acertos e 10 erros e d 0
acertos
6. Resolva: Uma pessoa aplicou a importância de R$ 500,00 em uma instituição
bancária que paga juros mensais de 3,5%, no regime de juros compostos. Quanto
tempo após a aplicação o montante será de R$ 3500,00?
Fórmula para o cálculo dos juros compostos: M = C * (1 + i)t
R: Nenhum aluno acertou a questão, alguns até tentaram substituir na fórmula, mas
ninguém chegou resposta.
31
Pós-teste
1. Resolva:
a) Log2 2
b) Log3 9
c) Log 100
d) Log5 25
e) Log2 32
R: Questão a 14 acertos e 1 erro, b 15 acertos, c 11 acertos e 4 erros, d 14 acertos e 1
erro e a questão e 12 acertos e 3 erros.
2. Resolva: Paulo aplicou R$ 800,00 num investimento que rende 3% a.m., a juros
compostos. Quanto tempo após a aplicação o saldo será de R$ 1.200,00?
Fórmula para o cálculo dos juros compostos: M = C * (1 + i)t
32
R: 7 acertos e 8 erros, mas a maioria substituiu na fórmula
3. Dê sua opinião sobre o uso da calculadora científica para resolver problema
utilizando Logaritmo
R: A maioria das respostas foi que a calculadora é muito útil e facilitadora e algumas
das respostas foi que gostaram bastante.
33
8. CONSIDERAÇÕES FINAIS
Com a aplicação do pré-teste os alunos mostraram não lembrar, o conteúdo tanto que
acabaram bem rápido, uns até se sentiram envergonhados por não conseguirem fazer
o teste.
No dia seguinte marcamos para fazer a oficina sobre Logaritmo, como não tinha muito
tempo para a aplicação ser bem clara e objetiva, falei um pouco sobre a história do
Logaritmo, as condições de existência, alguns casos particulares do Logaritmo, como:
logaritmo da própria base e logaritmo com a base decimal, algumas propriedades,
como: o do produto e do quociente foi feitos alguns exercícios para que eles pudessem
usar a calculadora científica e foi feito também um exercício sobre matemática
financeira envolvendo logaritmo.
Os alunos fizeram alguns comentários, como: que gostaram muito da oficina até uma
aluna que tinha dito no pré-teste que não havia visto esta matéria disse que
compreendeu o assunto e agradeceu pela oportunidade de poder ver um pouco sobre o
assunto naquele momento.
Marcamos o pós-teste para a próxima semana na terça-feira, e disseram que eu
poderia ter certeza que eles iriam melhor no próximo teste com a explicação que
tiveram.
Os alunos fizeram com bastante calma o pós-teste, havia exercícios iguais ao do préteste e alguns diferentes, mas tudo dentro do que eu havia passado para eles na oficina
foi bem tranquilo aplicação do pós-teste.
34
9. REFERÊNCIAS
BAUMGART, JOHN K. História da Álgebra, São Paulo: Editora Atual, 1992.
BOYER, CARL B. História da Matemática. São Paulo: Edgard Blucher, 1974.
D’AMBROSIO, U. Etnomatemática, elo entre as tradições e a modernidade. Belo
Horizonte: Autêntica, 2001.
EVES, HOWARD. Introdução à História da Matemática. Campinas: Ed. Da UNICAMP,
1995.
FACCHINI, WALTER. Matemática Volume 1. São Paulo: Editora Saraiva. 1º Edição –
1996.
J. STRUIK, DIRK. História Concisa das matemáticas. Gradiva, Lisboa. Editora Ciência
Aberta, 1992.
LIMA, ELON LAGES. Logaritmos. Brasília: Sociedade Brasileira de Matemática, 1980.
SÃO PAULO, SECRETARIA DA EDUCAÇÃO. Caderno do professor: matemática,
ensino médio – 1ª série, v.3. São Paulo: SEE, 2009.
35
SOUZA, SARAH RABELO DE. A Calculadora no ensino de matemática: estudo de caso
em uma escola técnica de 2º grau. Marília: UNESP, 1996 (Dissertação de Mestrado).
www.educ.fc.ul.pt/icm/icm99/icm44/historia.htm - Um pouco de história. livro.gif (4074
bytes). Os logaritmos foram inventados por John Napier, de modo a simplificar os
processos de multiplicação e divisão. Acesso em 25/07/2011.
ecalculo.if.usp.br/funcoes/logaritmica/historia/hist_log.htm - Um pouco da História dos
Logaritmos. Acesso em 30/08/2011.
valordaciencia.blogspot.com/.../um-pouco-da-historia-do-l... - Um pouco da história do
logaritmo. Acessado em 30/08/2011
http://www.brasilescola.com/matematica/aplicacoes-dos-logaritmos.htm.
30/08/2011.
Acesso
em