FMC_Cap7.2_slides

Capítulo VII 2
Capítulo VII.2
Magnetismo
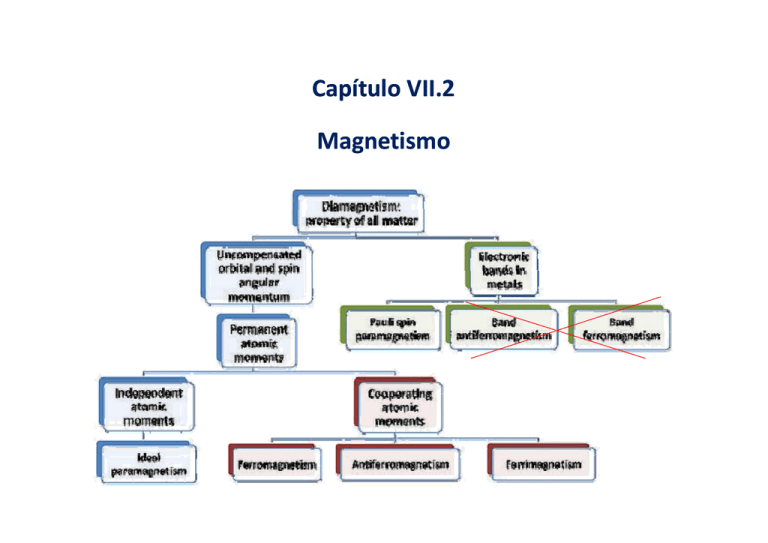
 Consideram‐se os momentos magnéticos isolados
 As interacções dos momentos magnéticos entre si ou com as suas vizinhanças
não são consideradas
 Consideram‐se os átomos isolados e as suas interacções com um campo
magnético aplicado
MOMENTOS MAGNÉTICOS DE SÓLIDOS
 Sólido com camadas completas
L=0 S=0  J=0 
L=0, S=0 
J=0  momento magnético nulo
momento magnético nulo
Ex.: gases inertes, iões com camadas preenchidas
 Sólidos covalentes
Momentos magnéticos atómicos diferentes de 0
Sólido: momento magnético NULO
DIAMAGNETISMO: DIAMAGNETISMO
<0
ou
PARAMAGNETISMO
: >0
 Magnetismo fraco
 Metais de transição, lantanídeos, actinídeos
 Estruturas magnéticas ordenadas
Estruturas magnéticas ordenadas
FERROMAGNETISMO
ANTIFERROMAGNETISMO
etc.
t
INTERACÇÕES ENTRE ELECTRÕES NO ÁTOMO
(i) Interacção electrostática
I t
ã l t táti
a) de cada electrão com o núcleo
b) dos electrões entre si
dos electrões entre si
(ii) Interacção magnética
V( i)
V(r
 2 2 Ze2
e2
 i  r    IM
i
2m
j i rij
‐ do spin dos electrões com o seu momento orbital
‐ do spin dos electrões entre si (muito pequena) a)
b)
IM –– interacção spin
IM interacção spin‐‐orbital
pequeno
q
‐ os Li e os Si estão fortemente acoplados
p
combinando‐se dando L e S
IM p
total para o átomo; só depois L e S se combinam e dão um J total  as
interacções electrostáticas tem grande importância  acoplamento L‐S
IM grande – a interacção spin‐orbital é forte: os Li e Si combinam‐se dando Ji; só
depois os Ji se combinam dando J  acoplamento J‐J
 A orientação da órbita de um dado electrão
é caracterizada pelo momento angular orbital
MOMENTOS MAGNÉTICOS DE ÁTOMOS ISOLADOS

Considerando um átomo isolado num campo magnético :
B
Cada electrão, além do momento magnético de spin, tem um momento dipolar Cada
electrão além do momento magnético de spin tem um momento dipolar
magnético / momento angular orbital.

 
O momento angular total do átomo é: L   ri  pi
i
2
p

ˆ
i
 Vi 
Na ausência de campo o Hamiltoniano do átomo é: Hˆ 0   

i  2m


Z
Na presença de um campo o Hamiltoniano passa a escrever‐se:
  e2

  2
B  ri 
Hˆ  Hˆ 0   B L  gS  . B 

8m i
perturbação de 1ª ordem
termo paramagnético
termo diamagnético
DIAMAGNETISMO
Todos os materiais apresentam uma contribuição diamagnética para  
classicamente, explicado através da lei de Lenz  aplicando um campo
magnético surge uma corrente induzida cujos efeitos se opõem à variação de
fl
fluxo
d id à aplicação
devida
li ã do
d campo
Pequena magnetização induzida pelo campo aplicado
<0 (pequena, 10‐5)
Lei de Lenz

M
M
 0
0
H
B
São diamagnéticos  materiais com átomos “não magnéticos”
 os gases raros
 a maioria dos gases poliatómicos: H2, N2, …
 os sólidos iónicos
ólid ió i
 os supercondutores (diamagnetes perfeitos: =‐1)
SUSCEPTIBILIDADE MAGNÉTICA
 Resultado de cálculo clássico (!?)
Ne 2 ZR 2
   0
6m
Z
2
2
N átomos, com Z electrões, distribuição esférica de raio R    rn  ZR 
n

 Resultado de cálculo rigoroso ( a partir do termo “diamagnético” do
hamiltoniano)
N e 2 0 Z
 
 ri  2

V 6m i 1
Sólido com N átomos, cada um com Z electrões
 É preciso conhecer a distribuição electrónica (i.e., a função de onda …)
Aproximação:
A
i
ã
S Zef número
Se
ú
d electrões
de
l t õ na última
últi
camada e <ri2> constante para todos os electrões desta
camada
 resultado clássico
<0 e independente de T
DIAMAGNETISMO DE SUPERCONDUTORES
PARAMAGNETISMO
São paramagnéticos  materiais cujos átomos têm momentos magnéticos
permanentes
M
M
   0  0  interacção pequena (quase nula) entre momentos
B
H
magnéticos vizinhos  distribuição aleatória
 pequena magnetização induzida por um campo aplicado
>0 e pequeno ( 10‐33‐10
10‐55 à temperatura ambiente)
SUSCEPTIBILIDADE MAGNÉTICA
 Materiais
M
i i cujos
j
á
átomos
têm
ê
momentos magnéticos
éi
permanentes
 Átomos com electrões desemparelhados
p



 Momento magnético atómico associado a J  L  S
 Efeito opostos de um magnético aplicado (alinhamento) e
da temperatura (vibrações atómicas  desalinhamento)
Resultado de um cálculo semiclássico

N 0 2

3 k BT
 Lei de Curie :  
1
T
 Cálculo para um sistema quântico (J)

0 n
3k BT
Lei de Curie
ef2

ef  J ( J  1) g J  B



3 S ( S  1)  L( L  1)
g J  
2
2 J ( J  1)

CAMPO CRISTALINO
 Interacção
I t
ã magnética
éti entre
t os átomos
át
magnéticos
éti
d um cristal
de
i t l e os átomos
át
magnéticos vizinhos
p cristalino é um campo
p electrostático criado p
pelos átomos vizinhos
 O campo
no cristal
Distribuição angular das orbitais
3d: os níveis dz2 e dx2‐y2 formam os
níveis eg. Os níveis dxy, dxz e dyz
formam os níveis t2g:
Átomo metálico Mn numa simetria octaédrica
e tetraédrica. A simetria octaédrica é muito
comum em óxidos
ó id de
d metais
i de
d transição
i ã com
os átomos de oxigénio localizados nos vértices
e o átomo metálico no centro
Campo cristalino resultante
da interacção electrostática:
a orbital dxy corresponde
p
a
menor energia do que a
orbital dx2‐y2
 CONGELAMENTO DO MOMENTO ORBITAL
1/ 2




p

g
J
J

1
Porque não concordam os valores calculados de 1
com
J
os medidos experimentalmente para os iões de metais de transição?
Nestes casos a interacção spin‐orbital é mais fraca que o campo cristalino
 3ª regra de
d Hund
H d não
ã é válida
álid
Os valores experimentais sugerem, para o estado fundamental de iões 3d:
L  0 ( J  S g J  2)
ef  2B S (S 1)
Diz‐se que o “momento orbital está CONGELADO”
Os valores de pexp concordam melhor com os valores
p2  2S S 1
1/ 2
Nas terras raras – iões 4f – os
electrões 4f não são os mais
exteriores; são “blindados”
pelos electrões 5p
 ACOPLAMENTO L‐S (Russell‐
Saunders) válido
INTERACÇÕES MAGNÉTICAS
Interacção magnética que permite os momentos magnéticos no sólido
comunicarem entre si, podendo originar ordem de longo alcance
átomo em geral J>0  distribuição
 Se os dois electrões pertencerem ao mesmo átomo,
espacial antisimétrica  menor energia de repulsão  electrões afastados (Jij=J)
 Se os dois electrões pertencerem a átomos vizinhos a situação é bem diferente
Jij=J
  Hamiltoniano
ˆ
 A energia de troca é de origem ELECTROSTÁTICA: H   J ij Si .S j
de
ij
Ferromagnete
Antiferromagnete
Heisenberg
Vidro de spin
Estrutura espiral
Estrutura helicoidal
TROCA DIRECTA
Interacção de troca entre electrões em átomos “magnéticos” vizinhos
e acção de oca e t e e ect ões e áto os ag ét cos
os
Só será efectiva se houver sobreposição significativa das orbitais em átomos vizinhos
 Não é o caso das terras raras (electrões 4f bastante localizados)
(
)
 Nos metais de transição com orbitais d mais extensas não é o único mecanismo de troca
TROCA INDIRECTA
Não há sobreposição (directa) das orbitais [3d de iões Mn
Não
há sobreposição (directa) das orbitais [3d de iões Mn2+ vizinhos]
Há uma troca indirecta entre iões que não são os vizinhos mais próximos
É mediada por um ião não magnético situado entre os dois iões magnéticos
p
g
g
 Situação que corresponde a maior deslocalização dos electrões magnéticos 
implica diminuição de energia cinética (partícula numa caixa de dimensão L,
energia  L‐2
 É um processo de 2ª ordem, tratado em teoria de perturbações de 2ª ordem
 A interacção de troca é um mecanismo de muito curto alcance. Por isso se
designa esta por SUPERTROCA
Mn O
TROCA INDIRECTA ‐‐ metais
TROCA INDIRECTA A interacção de troca é mediada pelos electrões de condução
é
l
l
MECANISMO: um momento magnético localizado (num ião magnético) polariza o
spin dos electrões; estes electrões acoplam com um momento
magnético a uma distância r – interacção RKKY (Ruderman, Kittel,
Kasuda & Yosida) ou de troca indirecta