Matemática Mod 2.pmd

www.alunonota10.com
Funções Trigonométricas I
Arco Trigonométrico
AP é o conjunto de todos os arcos de origem a e extremidade
Definição
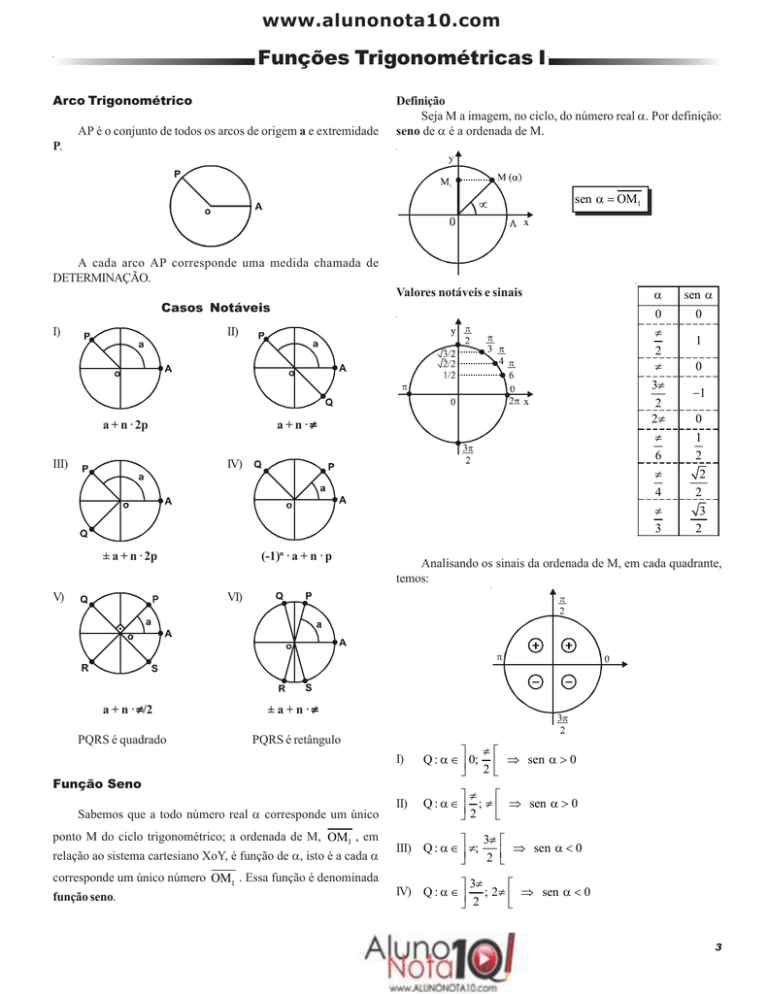
Seja M a imagem, no ciclo, do número real α. Por definição:
seno de α é a ordenada de M.
P.
sen α = OM1
A cada arco AP corresponde uma medida chamada de
DETERMINAÇÃO.
Valores notáveis e sinais
Casos Notáveis
II)
I)
III)
IV)
V)
0
π
2
π
0
π
4
π
3
(-1)n · a + n · p
± a + n · 2p
sen α
3π
2
2π
π
6
a+n·π
a + n · 2p
α
1
0
−1
0
1
2
2
2
3
2
Analisando os sinais da ordenada de M, em cada quadrante,
temos:
VI)
a + n · π/2
PQRS é quadrado
±a+n·π
PQRS é retângulo
I)
 π
Q : α ∈  0;  ⇒ sen α > 0
 2
II)
π 
Q : α ∈  ; π  ⇒ sen α > 0
2

Função Seno
Sabemos que a todo número real α corresponde um único
ponto M do ciclo trigonométrico; a ordenada de M, OM1 , em
relação ao sistema cartesiano XoY, é função de α, isto é a cada α
 3π 
III) Q : α ∈  π;
⇒ sen α < 0
2 

corresponde um único número OM1 . Essa função é denominada
função seno.
 3π

IV) Q : α ∈  ; 2π  ⇒ sen α < 0
 2

3
www.alunonota10.com
Funções Trigonométricas I
Representação Gráfica
Façamos x percorrer o intervalo [0; 2π] e vejamos o que
acontece com y = sen x. Isso equivale a fazer o ponto M, imagem de
x, dar uma volta completa sobre o ciclo, no sentido anti-horário,
partindo da origem 0, e observar como varia a ordenada de M.
As funções que se comportam de maneira semelhante ao seno,
isto é, repetem sua variação, são chamadas funções periódicas.
Definição:
Uma função f : A → B é periódica se existir um número
positivo p que satisfaz a condição: f(x + p) = f(x) para todo x ∈ A.
O menor valor positivo de p chama-se período da função f.
Intuitivamente, o período é o comprimento do menor intervalo no
qual a função passa por um ciclo completo de variação.
Observando o gráfico, vemos que o período da função seno é
p = 2π. Para todo x, semo:
sen x = sen (x + 2π) = sen (x + 4π) = …
Função Cosseno
Sabemos que a todo número real α corresponde um único
ponto M do ciclo trigonométrico; a abscissa de M, OM2 , em
relação ao sistema cartesiano XoY, é função de α, isto é, a cada α
Fazendo um diagrama com x em abscissas e y = sen x em
ordenadas, podemos representar os pares (x; sen x) da tabela anterior
por pontos e ligá-los para obter parte do gráfico da função seno,
chamado senóide:
corresponde um único número OM2 . Essa função é denominada
função cosseno.
Definição
Seja M a imagem, no ciclo, do número real x. Por definição:
cosseno de α é a abscissa de M.
cos a = OM2
α
sen α
0
π/2
1
0
∀x ∈ R, ∃sen x e -1 ≤ sen x ≤ 1
π
3π / 2
2π
−1
0
1
e vice-versa
30°
3
2
2
2
1/ 2
Valores notáveis e sinais
Domínio e Conjunto Imagem
O domínio da função é R e a imagem é o intervalo [-1; 1], isto
significa que:
∀ y ∈ [−1; 1], ∃ x ∈ R tal que sex x = y.
Observemos que, como o domínio da função seno é R, a
senóide continua à direita de 2π e à esquerda de O. Na figura está
representada apenas uma parte do gráfico.
Função Periódica
A partir de 2π a função seno começa a repetir os seus valores:
4
45°
60°
Analisando os sinais da abscissa de M em cada quadrante,
temos:
www.alunonota10.com
Funções Trigonométricas I
I)
 π
Q : α ∈  0;  ⇒ cos α > 0
 2
II)
π 
Q : α ∈  ; π  ⇒ cos α < 0
2

sen (-x) = -sen x
cos (-x) = cos x
 3π 
III) Q : α ∈  π;
⇒ cos α < 0
2 

 3π

IV) Q : α ∈  ; 2π  ⇒ cos α > 0
 2

Representação Gráfica
Se fizermos x percorrer de 0° a 360° e observarmos como varia
a abscissa de M teremos:
para todo x, concluímos que o seno é função ímpar e o cosseno é
função par.
Reconhecimento
Uma função é par quando o seu gráfico é simétrico em relação
ao eixo das ordenadas (verifique que, numa função par, pontos de
abscissas opostas têm a mesma ordenada).
Uma função é impar, quando o seu gráfico é simétrico em
relação à origem do sistema cartesiano (verifique que, numa função
ímpar, pontos de abscissas opostas têm ordenadas também
opostas).
Gráficos
Seja uma função do tipo: y + a + b · trig (c x + d), vamos
observar o que os números reais a, b, c e d fazem com o gráfico:
Fazendo um diagrama com x em abscissas e y = cos x em
ordenadas podemos representar os pares (x; cos x) por pontos de
um plano cartesiano e ligando-os obtemos partes do gráfico função
cosseno, chamado cossenóide:
1)
2)
3)
Observemos que:
o domínio da função cosseno é R.
a imagem é o intervalo [-1; 1].
a função cosseno é periódica e de período p = 2π.
Exemplo 1: Construa o gráfico da função y = 1 + sen x e dê o
seu domínio, imagem e período.
Sugestão: primeiro construa o gráfico da função y = sen x, já
conhecido.
Em seguida observe o sinal de a: Se a é positivo, no caso 1,
levante todos os pontos do gráfico uma unidade, mas, se a for
negativo, abaixe todos os pontos de uma unidade.
Note que o período continua o mesmo p = 2π, o mesmo
acontece com o domínio que continua sendo R, só a imagem é que
mudou, passará de [-1; 1] para [-1 + a; 1 + a], isto é, [0; 2].
Exemplo 2: Construa o gráfico da função y = 2 · sen x e dê o
domínio, imagem e período.
Função Par e Função Ímpar
Dizemos que uma função:
• f : A → B é par se f(-x) = f(x), para todo x, x ∈ A.
• f : A → B é impar se f(-x) = -f(x) para todo x, x ∈ A.
Observe que os números x e -x têm, no ciclo, imagens simétricas
em relação ao eixo das abscissas. Então temos:
5
www.alunonota10.com
Funções Trigonométricas I
Sugestão: construa o gráfico de y = sen x, em seguida
multiplique os valores notáveis de y por b, no caso 2, depois una
os pontos multiplicados e o gráfico já estará pronto.
Note que mais uma vez o período e o domínio não se alteram,
só a imagem, assim de [-1; 1] para [-1 · b; 1 · b], no caso Im = [-2; 2].
04. Esboçar o gráfico de y = |sen x| e dar o seu conjunto imagem.
05. Determine m de modo que se tenha cos x = m − 3 .
2
06. Esboçar o gráfico da função y = 1 +
Exemplo 3: Construa o gráfico da função y = sen 2 · x, e dê o
domínio, a imagem e o período da função:
+ 2cos x e dar o seu
conjunto imagem.
01. Resolva as equações:
a) sen x = -1
2π
,
Sugestão: primeiro calcule o novo período, que será p =
c
2π
= π , divida este valor por quatro e desenhe a senóide.
2
Note que nem a imagem, nem o domínio foram alterados,
somente o período.
isto é, p =
π

Exemplo 4: Construa o gráfico da função y = sen  x −  , e
4

dê o domínio, a imagem e o período da função:
b) cos x = 1
c) cos x = 0
02. Determine m para que tenham soluções as equações:
a) sen x = m - 1
c) m² + cos x = 1
b) cos x = 2m² - 3m - 1
03. Determine o período das funções:
a) y = sen 4x
d) y = 2cos x
b) y = sen (3x - n)
e) y = 3 + cos 2x
c) y = cos x/4
f) y = 7sen πx
04. Dê o valor máximo e o mínimo que y pode ter em cada caso:
a) y = 7sen x + 3
b) y = 5 · cos x
c) y = 2 + sen² x
2π 
x
 a 
05. Calcule a sabendo-se que o período da função y = sen 
é igual a
3π
.
2
06. Diga quais das funções abaixo são pares e quais são ímpares.
Observe que d não influi na imagem e nem no período da
função, mas acarreta um deslocamento da senóide no eixo x, da
seguinte maneira: se d > 0 desloca a senóide, d para a esquerda, e
se d < 0 desloca a senóide d para a direita, é o caso do nosso
exemplo:
Resumo:
- O domínio será sempre R, para quaisquer valores de a, b, c e
d.
- O período só será alterado pelo valor de c, p =
a) f(x) = x² + 1
d) f(x) = cos 2x

01.
a) S =  x ∈ R x =


c) S =  x ∈ R x =

02.
01. Determine k de modo que se verifique sen x = 3k + 1.
imagem.
6
05.
06.
π

+ k π, k ∈ Z 
2

a) 0 ≤ m ≤ 2
b) -1/2 ≤ m ≤ 0 ou 3/2 ≤ m ≤ 2
c)
03. Esboçar o gráfico da função y = 2sen x e dar o seu conjunto
3π

+ 2kπ, k ∈ Z 
2

b) S = {x ∈ R | x = 2kπ, k ∈ Z}
03.
04.
02. Dar o domínio, o conjunto imagem e o gráfico de y = 1 + sen x.
c) f(x) = x² + 2x + 1
f) f(x) = log x
Gabarito:
2π
.
c
- A imagem só é alterada pelos valores de a e b.
b) f(x) = 3x
e) f(x) = 3sen x
− 2≤m≤ 2
a) π/2
b) 2π/3
c) 9π
a) máximo: 10, mínimo: -4
b) máximo: 6, mínimo: 4
c) máximo: 3, mínimo: 2
a = 3/2
pares: a, d ímpares: b, e
d) 2π
e) π
f) 4π