Circuitos de corrente alternada e sistema por - dsee

ET720 – Sistemas de Energia Elétrica I
Apêndice
Revisão de circuitos de corrente alternada e sistema por unidade
A.1
Circuitos de corrente alternada
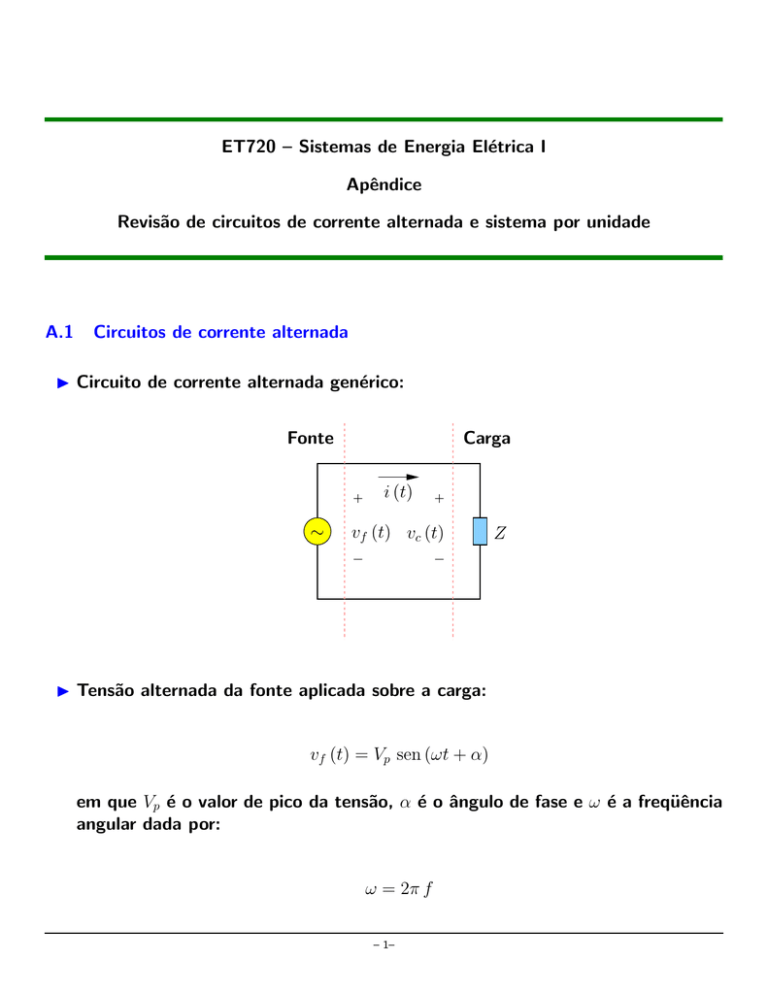
I Circuito de corrente alternada genérico:
Carga
Fonte
PSfrag replacements
+
∼
i (t)
+
vf (t) vc (t)
−
Z
−
I Tensão alternada da fonte aplicada sobre a carga:
vf (t) = Vp sen (ωt + α)
em que Vp é o valor de pico da tensão, α é o ângulo de fase e ω é a freqüência
angular dada por:
ω = 2π f
– 1–
No Brasil, f = 60Hz → ω = 377rad/s. O valor eficaz da tensão é:
√
Vp = 2 Vef
I Corrente elétrica que circula pela fonte e pela carga:
i (t) = Ip sen (ωt + β)
√
em que Ip é o valor de pico da corrente e β é o ângulo de fase. Ief = Ip/ 2 é
o valor eficaz da corrente.
I As formas de onda de tensão e corrente podem ser representadas na forma
fasorial, em que as expressões no tempo são substituı́das por números
complexos (fasores):
√
2 Vef sen (ωt + α)
n√
o
j(ωt+α)
==
2 Vef e





√
jα jωt
2 Vef e e
==
| {z }




v (t) =
V~
em que o fasor V~ é um número complexo com módulo igual ao valor eficaz da
tensão Vef e ângulo igual ao ângulo de fase da tensão α. Pode-se escrever:
~ = Vef ejα = Vef ∠α V
V
Para a corrente:
I~ = Ief ejβ = Ief ∠β A
– 2–
I Diagrama fasorial:
V~
PSfrag replacements
α
β
I~
I A relação entre os fasores de tensão na carga e corrente pela carga é definida
como a impedância da carga:
Z=
~
Vef
V
=
∠ (α − β) =| Z | ∠φ = R + jX Ω
Ief
I~
em que R é a resistência e X é a reatância. Se a carga tiver caracterı́stica
indutiva X e φ serão positivos. Se a carga tiver caracterı́stica capacitiva X e φ
serão negativos.
I A potência entregue à carga pela fonte é:
p (t) = v (t) · i (t)
= Vef Ief cos (φ) [1 − cos (2ωt)] − Vef Ief sen (φ) sen (2ωt)
= P [1 − cos (2ωt)] −Q sen (2ωt)
|
{z
}|
{z
}
A
B
– 3–
Observações:
−π/2 ≤ φ ≤ π/2
A → potência ativa instantânea
P = Vef Ief cos φ = valor médio de p (t) = valor médio de A
P só existe quando há elementos resistivos no circuito (φ 6= ±π/2)
P ≥ 0, para qualquer φ
B → potência reativa instantânea
Q = Vef Ief sen φ = valor de pico de B
Q só existe quando há elementos reativos no circuito (φ 6= 0)
Q ≥ 0 para 0 ≤ φ ≤ π/2 (carga indutiva → consome potência reativa)
Q ≤ 0 para −π/2 ≤ φ ≤ 0 (carga capacitiva → fornece potência reativa)
I Definição – potência complexa:
~ I~∗
S=V
= Vef ∠α Ief ∠ − β
= Vef Ief ∠ (α − β)
= | S | ∠φ
= Vef Ief cos φ + j Vef Ief sen φ
= P + j Q VA
P
– potência ativa (W)
Q
– potência reativa (var)
| S | – potência aparente (VA)
– 4–
Exemplo
Considere o circuito a seguir e mostre que a potência instantânea entregue ao
resistor é igual ao termo A e a potência instantânea entregue ao indutor é igual
ao termo B na expressão da potência instantânea.
i (t)
PSfrag replacements
+
v (t) =
√
2 Vef sen (ωt) V
ir (t)
R
ix (t)
X
−
Fasor de tensão:
~ = Vef ∠0◦ V
V
Corrente pelo resistor:
~
V
Vef ◦
I~r =
=
∠0 = Ir ∠0◦ A
R
R
Corrente pelo indutor:
V~
Vef
=
∠ − 90◦ = Ix ∠ − 90◦ A
I~x =
jωL
X
– 5–
Diagrama fasorial:
PSfrag replacements
I~r
V~
φ
I~x
I~
Formas de onda das correntes no domı́nio do tempo:
√
ir (t) = 2 Ir sen (ωt)
√
ix (t) = 2 Ix sen (ωt − 90◦)
Potência instantânea no resistor:
pr (t) = v (t) ir (t)
= 2 Vef Ir sen2 (ωt)
= Vef Ir [1 − cos (2ωt)]
Pelo diagrama fasorial, Ir é a projeção de I no eixo real:
pr (t) = Vef I cos φ [1 − cos (2ωt)]
que é igual ao termo A da expressão geral da potência instantânea.
– 6–
Para o indutor:
px (t) = v(t) ix(t)
= 2 Vef Ix sen (ωt) sen (ωt − 90◦)
= −2 Vef Ix sen (ωt) cos (ωt)
= −Vef Ix sen (2ωt)
= −Vef I sen φ sen (2ωt)
que é igual ao termo B da expressão geral da potência instantânea.
I Circuitos trifásicos:
em condições normais de operação → equilibrado (fontes e cargas);
cargas monofásicas são distribuı́das de forma a manter o equilı́brio;
tensões têm mesmo valor eficaz e são defasadas de 120◦;
correntes têm mesmo valor eficaz e são defasadas de 120◦;
pode-se calcular as grandezas de interesse somente para uma fase (em
função das observações anteriores) → diagrama unifilar;
I Potências em circuitos trifásicos:
√
P = 3 Vf If cos φ = 3 Vl Il cos φ
√
Q = 3 Vf If sen φ = 3 Vl Il sen φ
em que φ é o ângulo da impedância e os subscritos f e l indicam valores de
fase e de linha, respectivamente. As expressões acima independem da forma
como a carga e a fonte estão conectadas.
– 7–
Exercı́cio
Um motor, modelado como uma carga em Y equilibrada com impedância
10∠20◦ Ω por fase é alimentado por uma fonte cuja tensão de linha é de 173 V.
Calcular a corrente fornecida à carga, o fator de potência da carga e as potências
aparente, ativa e reativa consumidas pela carga.
(Resposta: 10 A; 0,94; 3 kVA; 2,82 kW; 1,03 kvar).
Exercı́cio
Uma tensão de linha de 4,4 kV é aplicada sobre uma carga conectada em Y
consistindo de três impedâncias iguais de 20∠30◦ Ω. A impedância de cada uma
das três linhas que conectam a carga ao barramento da subestação é 1, 4∠75◦ Ω.
Determinar a tensão de linha no barramento da subestação. Determinar também
o fator de potência visto pela fonte e a potência aparente fornecida pela fonte.
(Resposta: 4,62 kV; 0,84; 1,02 MVA).
– 8–
A.2
Sistema por unidade (pu) – revisão
I Quatro grandezas fundamentais: tensão, corrente, potência e impedância.
I Sempre que duas forem definidas, as outras duas podem ser obtidas.
I Idéia básica: exprimir as grandezas fundamentais de forma normalizada, ou
seja, exprimir cada grandeza como uma fração de grandezas fixadas
arbitrariamente, chamadas de grandezas de base:
grandeza em pu =
grandeza na unidade apropriada
valor de base
I Os valores de base são números reais → os módulos de números complexos
são expressos em pu e os ângulos de fase não são alterados.
– 9–
A.2.1
Circuitos monofásicos em pu
Exemplo
Considere
o circuito
a seguir.
PSfrag
replacements
0,024 Ω
0,08 Ω
I
∼
100 kVA
200 V
fp = 80% atrasado
E
Os seguintes valores de base são definidos arbitrariamente:
Sb = 100 kVA
Vb = 200 V
As outras duas grandezas fundamentais (corrente e impedância) ficam
automaticamente determinadas:
Sb
= 500 A
Vb
Vb
Zb =
= 0,4 Ω
Ib
Ib =
– 10–
Basta dividir cada grandeza do circuito pela sua respectiva grandeza de base e
PSfrag replacements
obter o circuito em pu:
0,06 pu
0,2 pu
i
∼
sc = 1 pu
vc = 1 pu
fp = 80% atrasado
e
Os cálculos são realizados em pu. Como a carga tem fator de potência 80%
(atrasado, carga indutiva), a potência complexa em pu é definida como:
sc = 1 ∠36, 87◦ pu
Assumindo a tensão na carga como nominal (200 V) e também como referência
angular do circuito:
vc = 1 ∠0◦ pu
A corrente pelo circuito é dada por:
∗
sc
= 1 ∠ − 36,87◦ pu
i=
vc
A tensão da fonte é dada por:
e = vc + z i = 1,1746 ∠6,06◦ pu
em que z é a impedância que conecta a carga à fonte. A tensão da fonte é
portanto de 234,9127 V (multiplicando o valor em pu pela tensão de base).
– 11–
As grandezas também são normalmente expressas em valores percentuais → a
resistência do circuito vale 0,024 Ω, 0,06 pu ou 6%.
A.2.2
Circuitos trifásicos em pu
I Para circuitos trifásicos equilibrados utiliza-se o modelo por fase
I Componente em Y → tomar uma fase do Y
Componente em ∆ → transformar em um Y equivalente e tomar uma fase do
Y equivalente
I Especialmente em estudos de geração e transmissão → assume-se circuito
equilibrado → modelo por fase → é como se fosse um circuito monofásico
I Em estudos relacionados com sistemas de distribuição, algumas vezes
considera-se como equilibrado. Outras, o desequilı́brio é importante e não
pode ser desprezado
I Escolha das bases → escolher valores adequados de tensão de fase e de linha
de base
– 12–
Exemplo
Uma fonte trifásica equilibrada de 220 V de linha alimenta uma carga conectada
em Y com impedância Z = 32,2 ∠60◦ Ω. Escolha as bases adequadas e calcular a
impedância da carga em pu.
Com relação à potência de base, pode-se arbitrar os valores:
Sbf = 1000 VA
e
Sbl = 3000 VA
em que Sbf é a potência de base por fase e Sbl é a potência de base total (3Sbf ).
Para as tensões, tem-se:
Vbf = 127 V
e
Vbl = 220 V
A escolha destes valores de base fazem com que em pu não haja diferença entre
os valores de fase e de linha, evitando as usuais confusões de cálculo.
A partir dos valores de base arbitrados, pode-se obter os outros valores de base:
Ibf =
=
Sbf
Vbf
Sbl /3
√
Vbl / 3
Sbl
= 7,8740 A
=√
3Vbl
– 13–
Zbf =
Vbf
Ibf
√
Vbl / 3
√
=
Sbl / 3Vbl
Vbl2
=
= 16,13 Ω
Sbl
A impedância da carga em pu fica:
z=
Z
32,2 ∠60◦
=
= 2 ∠60◦ pu
Zbf
16,13
O modelo em pu é idêntico a um circuito monofásico com uma fonte de 1 pu
alimentando uma carga da impedância z, resultando em uma corrente:
i=
1
= 0,5 ∠ − 60◦ pu
z
que transformada em unidades de corrente resulta em:
I = i Ibf = 3,94 ∠ − 60◦ A
– 14–
Referências
[1] C.A. Castro, M.R. Tanaka, Circuitos de corrente alternada: um curso
introdutório, UNICAMP, 1995.
[2] J.J. Grainger, W.D. Stevenson, Power System Analysis, McGraw-Hill, 1994.
[3] A.J. Monticelli, A.V. Garcia, Introdução a sistemas de energia elétrica,
Unicamp, 1999.
– 15–