Accionamento máquinas

Máquinas Eléctricas
Motores assíncronos
Accionamento de máquinas
Estudo do motor eléctrico, quando acoplado a uma máquina. A máquina accionada impõe duas
condicionantes ao arranque:
þ Binário resistente
þ Inércia das massas
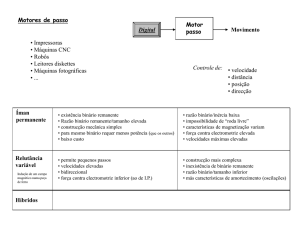
1. Binário resistente
O conhecimento do comportamento do
binário resistente, ao longo do processo de
arranque, é fundamental para o estudo deste
processo e para determinar o ponto de
funcionamento estável – velocidade e
potência nominais.
T
Binário
motor
Binário
resistente
O binário resistente é condicionado
pelas resistências passivas que, vistas do
eixo de accionamento, se traduzem no
binário necessário a ser fornecido, para que
aquelas sejam vencidas. Existem 4
mecanismos de fricção:
„
„
„
„
0
Ponto de
funcionamento
estável
10
% nS
Figura 2.1
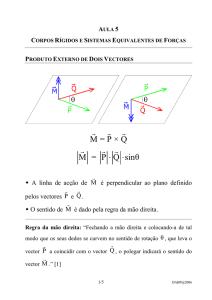
Coulomb – constante, para qualquer velocidade
Estática – importante a velocidade nula
Viscosa – originada por fluidos, é proporcional à velocidade
Fluída – originada por fluidos, cresce mais rapidamente que a velocidade
total
Coulomb
Viscos
a
Fluida
Figura 2.1
As máquinas accionadas reais têm, em maior ou menor grau, estes 4 tipos de fricção. As
figuras 2.3 a 2.6, representam os binários resistentes de vários tipos de máquinas.
1/10
Máquinas Eléctricas
Motores assíncronos
Veículos rápidos
Máquinas ferramentas
Compressor rotativo em carga
Elevação
Compressor alternativo em carga
Veículos lentos
Compressor rotativo em vazio
Calhandras de plásticos
Compressor alternativo em vazio
Extrusoras de plásticos
Figura 2.3
Figura 2.4
Bo
mb
as
/V
ent
ila
do
res
em
car
ga
Moínhos de bolas
s
ore
lad
i
t
en
/ V io
as vaz
b
m em
Bo
de
os
h
oín
M
os
ug
ríf
t
n
ce
Moínhos de martelos
Figura 2.5
Figura 2.6
Outras características de binários resistentes:
Æ Irregularidade do binário – oscilações do binário resistente, referidas ao binário médio, que
acontecem em máquinas com movimento alternado. São fontes potenciais de problemas de
ressonância mecânica no meio de ligação da máquina ao motor.
Æ Frequência de arranques – nº de arranques por unidade de tempo. São fonte de problemas
porquanto aumentam a concentração térmica nos motores.
Æ Inércia
2/10
Máquinas Eléctricas
Motores assíncronos
No anexo A, é fornecida uma tabela com estas características, para vários tipos de máquinas
accionadas.
Algumas máquinas mais usuais:
TM
Æ
Elevadores
Ascensores, montacargas e gruas
O binário é praticamente constante. Possuem um tambor
para converter o movimento rotacional em linear.
Aplicam-se as seguintes expressões:
v=ωr
r
v
m
F
Tr = m g r
Figura 2.7
quando exista um contrapeso (mcp) para compensar a carga
m à qual se adiciona a carga da cabine (mc), vem: mcp = mc + 0,5 m, sendo o
binário:
Tr = (m + mc – mcp) g r
A inércia que o elevador adiciona à inércia do motor é:
J = (m + mc + mcp) r2
Nas gruas eliminar-se-ão os valores de mc e mcp , os quais não existem.
Æ
Bombas e ventiladores
Exceptuando o binário de início (que oscila entre 5 e 20% do nominal), o binário
resistente que opõem ao motor é uma função parabólica de 2º grau da velocidade:
Tr = k n2
[n – rpm]
A potência nominal de ambas as máquinas é:
P = Q p/η
P – potência [kW]
Q – caudal [m3 /s]
p – pressão total na boca (bomba ou do ventilador) [N/m2 ]
η – rendimento (bomba ou ventilador)
A expressão da pressão difere de bombas para ventiladores:
ž Bombas
p=hg π
h – altura total gerada pela bomba com perdas de carga
g – aceleração da gravidade (9,81) [m/s2]
π – densidade do fluido [kg/m3]
ž Ventiladores
p=gh
h – pressão total = estática + dinâmica
3/10
Máquinas Eléctricas
Æ
Motores assíncronos
Bobinadoras e enroladoras
Máquinas diversificadas, embora todas respondendo a um padrão geral, pelo qual
o diâmetro da bobine cresce normalmente, tensionado com uma força constante,
diminuindo a sua velocidade angular – processo de enrolamento. No processo de
desenrolamento acontece o inverso. Assim:
F = cte
Tr
T
v = cte
raio grande:
- baixa velocidade angular
- alto binário
raio pequeno:
- alta velocidade angular
- baixo binário
ω
Tr = F r
ω
ω=v /r
e
Tr ω = F v = cte
r – raio da bobine (num instante
particular)
F – tensão do enrolado
v – velocidade linear do enrolado
Já que a tensão e a velocidade linear de enrolamento são fixas.
2. Inércia das massas
O momento de inércia, ou simplesmente inércia, é um conceito matemático que caracteriza
as propriedades dinâmicas dos volantes. Intuitivamente sabe-se que entre dois volantes com a
mesma massa, mas um deles mais largo axialmente e com menor diâmetro que o outro, se
comportam diferentemente nas acelerações e desacelerações – o de maior diâmetro demora mais a
acelerar e a desacelerar.
De acordo com a figura 2.9, o corpo gira em torno do seu eixo,
com velocidade ω. Sendo um corpo rígido, todos os seus elementos, de
massa dm, se movem com a mesma velocidade angular. Em cada
elemento de massa, verifica-se a equação do binário acelerador:
dT = r ⋅ dF = r ⋅ dm ⋅ dv
M
M
dt
= r ⋅ dm ⋅ r ⋅ d ω
= r ⋅ dm ⋅ d ω
d TM
dF M
r
2
dt
dt
v
dm
obtendo-se o binário total, integrando a todo o volume do sólido:
TM = ∫ dC M = ∫ r 2 ⋅ dm ⋅ dω = dω ⋅ ∫ r 2 ⋅ dm = J ⋅ dω
dt
dt
dt
Figura 2.9
Chamando inércia mássica, ou momento de inércia, de um corpo girante, ao integral:
m
J = ∫ r ⋅ dm
2
J – [kg.m2 ]
0
4/10
Máquinas Eléctricas
Motores assíncronos
Sistema com variação de velocidade
Muitas vezes existe a necessidade de adequar a velocidade da máquina accionada com a
velocidade do motor. Então, há que utilizar engrenagens, correias, polies, etc. Em princípio, não há
escorregamento entre engrenagem motora e engrenagem accionada.
Tal como se pode ver na figura 2.10, no ponto de
f1
contacto, existe equilíbrio de forças – f 1 = f 2 – donde, TM
poderemos igualar os binários motor e accionado:
r
r J
dω
1
TM − r1 f1 = J1
J2
dt
rf =J
2
2
2
dω
dt
f2
v
Também a velocidade linear é idêntica no ponto de
contacto:
Figura 2.10
v = r1ω1 = r2ω 2
Donde, associando estas equações, vem:

r 
T =  J +   ⋅ J

r 
2
1
M
1
2
 dω
⋅
 dt
1
2

ω 
T =  J +   ⋅ J

ω 
2
2
M
1
1
 dω
⋅
 dt
1
2
onde se verifica que a inércia J2 , no eixo de velocidade ω2 , se aproxima à inércia J1 , no eixo
de velocidade ω1 , corrigida, no entanto, pela relação:
r

r
1
2
 ω
 = 
 ω
2

 = i

2
2
1
sendo i, a relação de transmissão do sistema de engrenagens
2
Define-se inércia equivalente, referida ao eixo 1, como:
J = J + J ⋅  ω ω 


2
2
eq
1
2
1
5/10
Máquinas Eléctricas
Motores assíncronos
Arranque de máquinas
No arranque de motores de indução assíncronos, as quantidades que influenciam o
comportamento destas máquinas, são:
þ Tempo de arranque
þ Energia dissipada
þ Frequência dos arranques
Tempo de arranque
Considerando a inércia constante (caso mais frequente):
T − T = J ⋅ dω dt
M
r
integrando, vem:
ta =
ω =ω n
J
∫ T − T ⋅ dω
ω =0 M
r
Nota:
∫ ... ≡ soma
d ... ≡ diferença
embora este integral não seja de cálculo complicado, a dificuldade coloca-se nas funções de
TM(ω) e de Tr(ω), habitualmente complexas.
Por conseguinte, quando as funções de binário referidas são desconhecidas, pode utilizar-se um
método gráfico, explanado seguidamente:
i)
ii )
iii )
iv )
v)
vi )
Dividir o leque de velocidade em intervalos iguais
Ler, para o centro de cada intervalo de velocidade, os valores de TM e Tr
Calcular a diferença de binários (Ta =TM - Tr)
Dividir a inércia total J pelo binário de aceleração (Ta)
Multiplicar pelo incremento1 de velocidade (obtém-se o incremento de tempo, para cada intervalo)
Somar2 todos os incrementos (obtém-se o tempo total de aceleração)
É dado um exemplo no anexo B.
1
2
dω = incremento de velocidade
∫(J/T) x dω
6/10
Máquinas Eléctricas
Motores assíncronos
se Ta é constante num intervalo [1 ; 2], vem:
ta =
%T
J
Tacel
(ω 2 − ω1 )
%T
200
200
Tmotor
150
Taceleração
100
100
Tcarga
50
20
40
60
80
100
%
Figura 2.11
20
40
60
80
100
%
Figura 2.12
A integração da equação que dá o tempo de arranque, tem um caso particular, quando o binário
motor tem a expressão:
TM = Tmax
2
(s
smax
)+(
smax
s
)
o binário resistente, neste caso particular, torna-se Tr =0, vindo a integração do tempo de
arranque:
ta =

J ⋅ ω 0  1 − s2n
⋅
− smax ⋅ Lnep (sn ) 
2 ⋅ Tmax  s ⋅ smax

definindo a constante de tempo de arranque como:
TM = J ⋅
ω0
Tmax
que se interpreta como o tempo necessário para arrancar, aplicando durante todo o tempo o
binário máximo (Tmax), vindo então o tempo de arranque:
TM
ta =
2
2
 1 − sn

 2 ⋅ smax − smax ⋅ Lnep( sn ) 


7/10
Máquinas Eléctricas
Motores assíncronos
para se determinar o tempo t, decorrido até chegar ao ponto de escorregamento s, bastará
substituir ta por t e sn por s.
8/10
Máquinas Eléctricas
Motores assíncronos
Anexo A
9/10
Máquinas Eléctricas
Motores assíncronos
Anexo B
Supondo conhecidas as curvas de binário motor e máquina accionada (fabricantes)
Motor assíncrono, potência – 315 kW
Velocidade da máquina accionada – 992 rpm
Inércia conjunta – 70 kg.m2
TM - Tr
Tmotor
n
0
49,6
99,2
148,8
198,4
248,0
297,6
347,2
396,8
446,4
496,0
545,6
595,2
644,8
694,4
744,0
793,6
843,2
892,8
942,4
992,0
Tmáquina
T aceleração
dω
tacumulado
dt
1.750
350
1.400
10,39
0,52
0,52
1.830
100
1.730
10,39
0,42
0,94
2.010
175
1.835
10,39
0,40
1,34
2.275
340
1.935
10,39
0,38
1,71
2.600
560
2.040
10,39
0,36
2,07
2.965
835
2.130
10,39
0,34
2,41
3.450
1.170
2.280
10,39
0,32
2,73
3.800
1.560
2.240
10,39
0,32
3,05
3.750
2.000
1.750
10,39
0,42
3,47
3.000
2.500
500
10,39
1,45
4,92
4.000
3.500
1.000
900
2.500
800
velocidade [rpm]
3.000
2.000
1.500
1.000
500
700
600
500
400
300
200
100
0
1
2
3
T motor
4
5
6
T carga
7
8
9
10
T aceleração
0
0
1
2
3
4
5
tempo [s]
10/10