Aula 5

AULA 5
CORPOS RÍGIDOS E SISTEMAS EQUIVALENTES DE FORÇAS
PRODUTO EXTERNO DE DOIS VECTORES
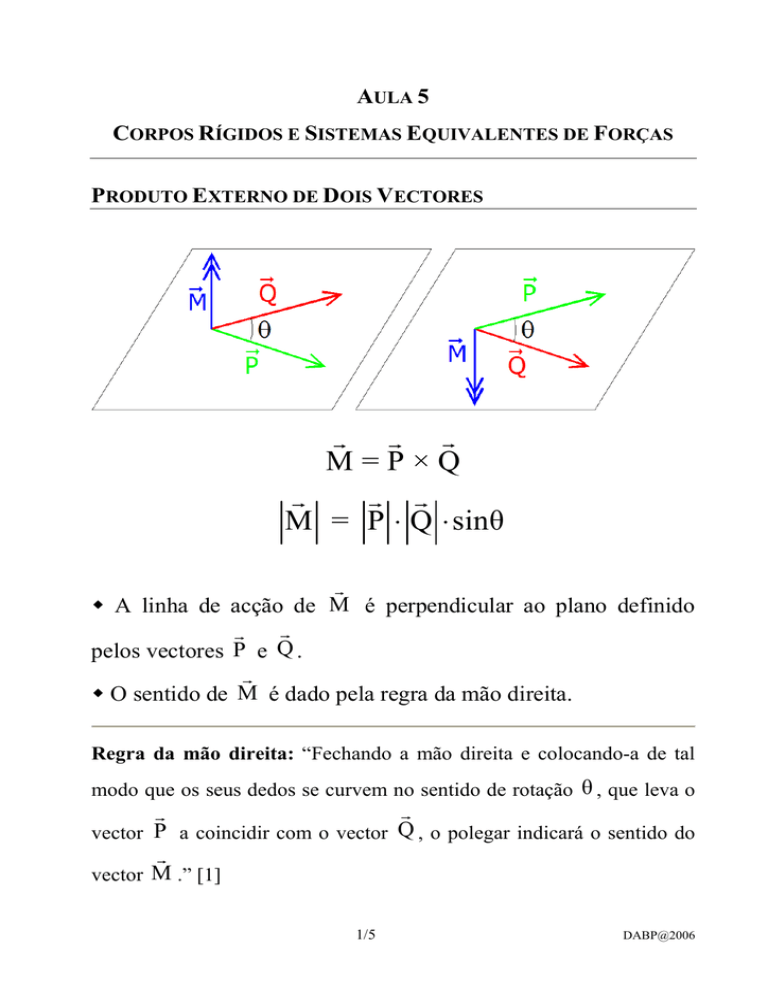
M=P×Q
M = P ⋅ Q ⋅ sinθ
A linha de acção de M é perpendicular ao plano definido
pelos vectores P e Q .
O sentido de M é dado pela regra da mão direita.
Regra da mão direita: “Fechando a mão direita e colocando-a de tal
modo que os seus dedos se curvem no sentido de rotação θ , que leva o
vector P a coincidir com o vector Q , o polegar indicará o sentido do
vector M .” [1]
1/5
DABP@2006
MOMENTO DE UMA FORÇA EM RELAÇÃO A UM PONTO
O momento de uma força define-se como o produto externo de
r por F .
M0 = r × F
M
O vector 0 é normal ao plano que contém os vectores r e F
e o seu sentido é dado pela regra da mão direita.
2/5
DABP@2006
MOMENTO DE UMA FORÇA EM RELAÇÃO A UM DADO EIXO
TEOREMA DE VARIGNON
A soma dos momentos de todas as forças de um sistema de
forças concorrentes em relação a um ponto, é igual ao momento
criado pela resultante do sistema em relação ao mesmo ponto.
M 0 = FX ⋅ d Y + FY ⋅ d X ( N ⋅ m )
ou
M0 = F ⋅ d ( N ⋅ m )
3/5
DABP@2006
BINÁRIO
Duas forças com a mesma intensidade, linhas de acção parale-
las e sentidos opostos formam um binário.
O único movimento que um binário pode provocar num corpo
rígido é a rotação.
SUBSTITUIÇÃO DE UMA FORÇA POR UMA FORÇA APLICADA
NUM PONTO O E UM BINÁRIO
1. colocar duas forças no ponto O, uma igual a F e outra igual a
-F ;
F
-F
2. substituir as forças e por um binário.
4/5
DABP@2006
F
“Qualquer força actuante num corpo rígido pode ser movi-
da para um ponto arbitrário O, desde que seja acrescentado um
binário de momento igual ao momento de F em relação ao ponto O.” [1]
O binário tende a produzir no corpo rígido a mesma rotação
em torno do ponto O que a força F tenderia a provocar antes de
ser deslocada para O.
REDUÇÃO DE UM SISTEMA DE FORÇAS A
UMA FORÇA E A UM BINÁRIO
BIBLIOGRAFIA
[1] Beer, Ferdinand P.; Johnston Jr., E. Russell; "Mecânica Vectorial
para Engenheiros - Estática"; Sexta Edição; McGraw Hill.
5/5
DABP@2006