Capítulo 1 - A PRODUÇÃO COLETIVA DO FRACASSO ESCOLAR

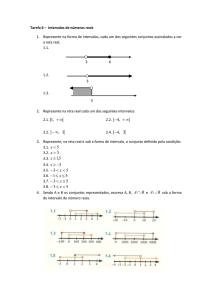
2. DADOS
Os dados são as informações obtidas através de observações, medidas,
respostas de pesquisas ou contagens em geral.
2.1 Classificação dos dados
Os dados podem ser classificados em:
Dados qualitativos: classificação por tipos ou atributos.
Exemplos:
A cor dos olhos (azuis, castanhos, verdes etc.) das modelos de uma determinada
agência.
Qualidade (defeituosa ou não defeituosa) de peças produzidas por uma máquina.
Grupo sanguíneo (A, B, AB ou O) dos alunos doadores de sangue da
Universidade.
Dados quantitativos: quando seus valores são expressos em números.
Exemplos:
O peso líquido de cada um dos sabonetes produzidos por uma empresa.
A altura dos alunos do 1º ano do Ensino Médio.
O diâmetro de parafusos produzidos por uma máquina.
2.2 Representação de dados em tabelas
Os dados podem ser apresentados através de uma tabela.
Dados isolados
No caso de dados qualitativos, a descrição através de uma tabela é muito
simples.
A tabela acima mostra o número de pessoas matriculadas em cada modalidade
de ensino; este número é denominado freqüência (fi).
Podemos também encontrar a freqüência relativa para cada modalidade; para
isso basta dividir a freqüência de cada modalidade pelo total de freqüências (n).
Veja o exemplo:
* arredondamento de duas casas decimais.
2.3 Distribuições de freqüências
Uma distribuição de freqüência é uma tabela de intervalos de classes com o
número total de entradas de dados em cada classe.
A freqüência (fi) de uma classe é o número de entrada de dados na classe.
Veja o exemplo.
A seguir, estão listados os salários, em reais, de cinqüenta funcionários de um
determinado setor de uma empresa automobilística:
2
500
1
800
6
00
7
50
3
000
00
3
3
700
2
650
3
700
2
000
800
2
2
100
1
3
600
2
100
800
200
2
1
800
1
2
900
1
090
600
750
2
1
550
1
2
700
9
80
490
300
2
3
250
2
1
650
1
050
450
880
2
3
100
5
1
900
9
50
20
900
1
3
900
1
2
980
7
00
200
100
9
3
800
1
2
3
6
80
800
800
500
2
200
2
800
3
800
3
100
Para organizar a tabela de salários, em reais, devemos construir uma tabela de
freqüências. Podemos observar que o menor salário é o de 520 e o maior é de 3900;
definimos então intervalos de classes iguais de 500 reais, ou seja, de 500 a 1000,
1000 a 1500 e assim por diante.
Observação: Uma fórmula utilizada para o cálculo do número de classes é:
K=1+3,222. log n, onde k é o número de classes, n é o número de elementos do
conjunto.
No exemplo acima temos: K=1+3,222. log 50 ≅6,47.
Embora exista uma fórmula para o número de intervalos de classe, muitos
pesquisadores determinam o número de intervalos dependendo da situação. Um
número de classes pequeno não é aconselhável, pois há perda de informação. Um
número de classes grande é desnecessário na maioria dos casos.
A freqüência (fi) neste caso é o número de funcionários que estão incluídos na
classe de salários.
Temos que ∑fi n , onde n é o número total de elementos da amostra.
Usamos a notação 500 |—1000, onde o intervalo é fechado à esquerda
(pertencem à classe os valores iguais ao extremo inferior) e aberto à direita (não
pertencem à classe os valores iguais ao extremo superior).
Amplitude do intervalo de uma classe é a diferença entre o limite superior e o
inferior.
Temos no exemplo 1000-500=500; logo, a amplitude do intervalo de classe é de
500 reais.
O Ponto médio de um intervalo de classe é a metade da soma do limite inferior
e o limite superior.
Veja o exemplo:
A freqüência relativa (fr) de uma classe é a freqüência (fi) desta classe dividida
pelo total de elementos da amostra(n).
A Freqüência Acumulada (fa) de uma classe é a soma da freqüência daquela
classe com a de todas as classes anteriores.
Veja o exemplo: