Exercícios sobre intervalos numéricos

Tópicos de Matemática Elementar:
Matemática Básica - Iniciação ao Cálculo
Exercícios sobre intervalos numéricos
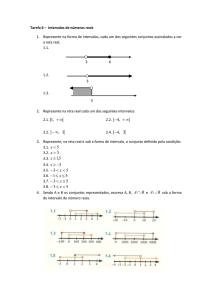
1. Represente gracamente os intervalos a seguir e verique se os números
5; π;
√
5; −0, 2;
5
;
2
pertencem a cada intervalo:
(a) A = [−2, 5)
(b) B = (2, 7)
(c) C = (6, +∞)
2. Sendo: A = [−2, 5), B = (2, 7) e C = (6, +∞). Determine:
(a) A ∩ C
(b) A ∩ B
(c) A − B
(d) A ∪ C
(e) (A ∪ C) ∪ B
(f) (A − C) ∩ B
3. Sendo U = R, represente cada um dos intervalos indicados por compreensão e na reta real:
(a) conjunto dos números maiores que -3 e menores que 1;
(b) conjunto dos números menores ou iguais a -4;
(c) conjunto dos números maiores que -1 ou menores que -3.
Respostas
INTERVALOS NUMÉRICOS
1.
Apresentamos aqui a representação de alguns intervalos numéricos:
(a, b) = {x ∈ R| a < x < b}
[a, b] = {x ∈ R| a ≤ x ≤ b}
√
5
5,−0.2, 2
√ 5
(b) 5,π , 5, 2
(a) π ,
(c) nenhum
2.
(a) ∅
(b) (2, 5)
(a, b] = {x ∈ R| a < x ≤ b}
[a, b) = {x ∈ R| a ≤ x < b}
(c) [−2, 2]
(d) [−2, 5) ∪ (6, +∞)
[a, +∞) = {x ∈ R| a ≤ x}
(e) [−2, +∞)
(−∞, b) = {x ∈ R| x < b}
(f) (2, 5)
3.
(a) {x ∈ R| − 3 < x < 1}
(b) {x ∈ R|x ≤ −4}
(c) {x ∈ R|x < −3 ou x > −1}
1