Viscosidade do Sangue

Viscosidade do sangue
P.J. Oliveira (UBI, Novembro 2009)
O sangue é uma suspensão de células (eritrócitos, leucócitos e trombócitos) em plasma. As
células que existem em maior quantidade são os eritrócitos, ou glóbulos vermelhos, sendo
determinantes para definir as propriedades reológicas do sangue. A sua concentração
volumétrica, o hematócrito H , varia consoante a temperatura e o estado de saúde da pessoa,
mas ronda os H = 42 − 45 % em situação normal. O sangue comporta-se como um fluido não
newtoniano, sobretudo para valores baixos da taxa de deformação ( γ < 100 s-1) e quando
circula em vasos de pequenas dimensões ( d ≤ 1 mm). Neste último caso o cariz bifásico da
suspensão, plasma com 45% de glóbulos vermelhos, torna-se notório. Isto acentua-se ainda
mais quando o diâmetro dos vasos é da mesma ordem de grandeza das dimensões dos
glóbulos vermelhos ( d gv = 8µ m) como acontece nos capilares.
Reofluidificação
Para se contabilizar o efeito de reofluidificação do sangue, ou seja, a diminuição da viscosidade
η com o aumento da taxa de deformação γ , usam-se modelos não newtonianos inelásticos
(sem elasticidade), também designados por modelos GNF (Generalized Newtonian Fluid).
Existem vários modelos empíricos deste tipo, e um deles é o modelo de Carreau-Yasuda,
definido pela equação:
a
η (γ ) = η∞ + (η0 − η∞ ) 1 + ( λγ ) 


n −1
a
Esta equação tem 5 parâmetros independentes que, para o caso do sangue, tomam os valores:
Viscosidade para taxa de corte nula: η0 = 0.056 Pa.s
Viscosidade para taxa de corte infinita: η∞ = 0.00345 Pa.s
Parâmetro Yasuda: a = 2
Tempo característico: λ = 3.313 s
Expoente: n = 0.3568
η(γ) (Ns/m2)
0.1
0.01
.
0.001
0.01
0.1
1
100
. 10
γ (1/s)
1000 10000
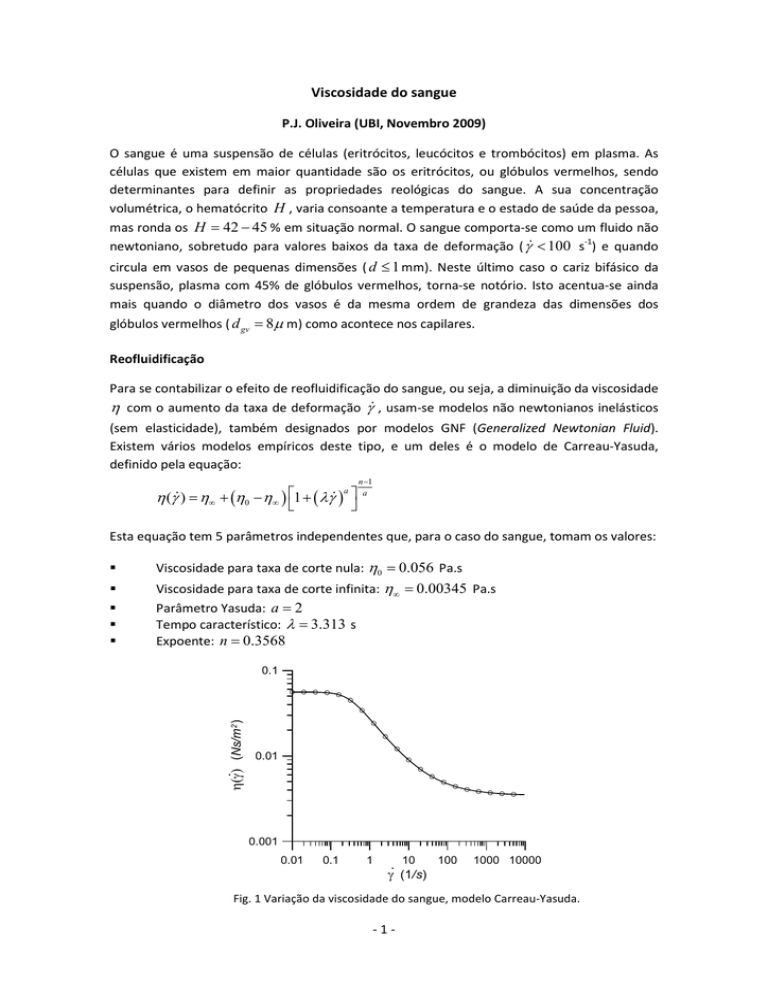
Fig. 1 Variação da viscosidade do sangue, modelo Carreau-Yasuda.
-1-
A Figura 1 mostra a variação da viscosidade em função da taxa de deformação de corte
prevista pelo modelo de Carreau-Yasuda. Para taxas de deformação baixas a viscosidade é
constante e igual ao valor de η0 . A partir de um certo valor de γ , dado aproximadamente
pelo inverso do tempo característico 1/ λ ( 1/ 3.13 = 0.30 1/s), a viscosidade começa a decair
segundo uma taxa determinada pelo expoente n . Quanto menor for n , maior é a inclinação
da variação da viscosidade em função de γ , a qual é dada por −(1 − n) em representação loglog.
Da definição do coeficiente de viscosidade de corte, obtém-se a tensão de corte:
τ = ηγ
A sua variação em escala logarítmíca é mostrada na Figura 2. Observa-se que para valores
elevados da taxa de corte a tensão vai aumentando linearmente, o que é característico do
comportamento newtoniano ( τ = µγ , µ constante).
100
τ(γ) (N/m2)
10
1
0.1
.
0.01
0.001
0.0001
0.01
0.1
1
100
. 10
γ (1/s)
1000 10000
Fig. 2 Tensão de corte em função da taxa de deformação para modelo Carreau-Yasuda.
A reofluidificação é mostrada de forma mais efectiva num gráfico em escala linear, como o da
Figura 3, que dá a tensão de corte do modelo Carreau-Yasuda com os mesmos parâmetros
dados acima. A diminuição do aumento da tensão de corte à medida que a taxa de
deformação aumenta é agora notória, sobretudo para baixos valores de γ . Fica também claro
que este modelo não tem tensão de cedência, uma vez que a tensão de corte tende para zero
quando γ → 0 .
-2-
1
τ(γ) (N/m2)
0.8
.
0.6
0.4
0.2
0
0
40
80.
120
160
200
γ (1/s)
Fig. 3 Tensão de corte versus taxa de corte em escala linear: modelo Carreau-Yasuda. Reofluidificação.
Efeitos de hematócrito e temperatura
Quando as taxas de deformação são elevadas, o sangue pode considerar-se como uma
suspensão de “partículas” num fluido newtoniano. Einstein deduziu uma equação que dá a
viscosidade da suspensão quando as partículas são esféricas e a sua concentração volumétrica
φ é pequena ( φ ≤ 0.05 ) e que, quando aplicada ao sangue, se escreve:

1 

 1 − αφ 
η = ηP 
Aqui η é a viscosidade do sangue, η P é a viscosidade do plasma (η P ≈ (1.2 − 1.8)η agua ;
η P ≅ 1.24 ×10−3 Pa.s a 37ºC) e α é um parâmetro que depende da forma geométrica das
partículas, sendo α = 2.5 para esferas como na lei de Einstein. Para valores mais elevados de
concentração φ , ou seja do hematócrito H = 100φ no caso do sangue, este parâmetro varia
não só com a própria concentração mas também com a temperatura. A seguinte correlação
empírica permite obter α numa gama limitada de concentrações:

α = 0.076 exp  2.49φ +

1107 −1.69φ 
e

T (K )

para 0.05 ≤ φ ≤ 0.6 .
A Figura 4 mostra a variação de viscosidade do sangue prevista com este modelo, onde se usou
para viscosidade do plasma o valor acima indicado (0.00124 Pa.s) e para temperatura o valor
normal do corpo humano, 37ºC, ou seja T = 310 K. Verifica-se que a viscosidade aumenta
exponencialmente com o aumento do hematócrito, até valores de H = 60% ( φ = 0.60 ) que
correspondem já a estados patológicos (policitemia). Na gama normal de valores do
hematócrito, quando H passa de 40 para 50%, a viscosidade aumenta de 28%. Este aumento
de viscosidade implica trabalho adicional para bombear o sangue. Por outro lado, quando a
temperatura sobe de 37ºC para 40ºC, com H = 45% constante, a viscosidade decresce de
2%.
-3-
viscosidade (Ns/m2)
0.005
0.004
0.003
.
0.002
0.001
0
20 .
40
Hematócrito (%)
60
Fig. 4 Variação da viscosidade do sangue em função do hematócrito (concentração volumétrica dos
glóbulos vermelhos), para temperatura de 37ºC.
Tensão de Cedência
Quando o sangue está em repouso, existe tendência para os glóbulos vermelhos se
aglomerarem formando estruturas. Estas estruturas opõem-se ao movimento quando uma
tensão relativamente pequena é aplicada. Por isso o sangue é um fluido que apresenta tensão
de cedência, isto é, uma tensão abaixo da qual o sangue não se deforma. Um modelo GNF
incorporando tensão de cedência e que tem sido muito utilizado para descrever a viscosidade
do sangue é o modelo de Casson, definido pelas equações:
τ = τ 0 + η∞γ
γ = 0
se τ ≥ τ 0
se τ ≤ τ 0
A tensão de cedência τ 0 depende do hematócrito, assim como o coeficiente de viscosidade da
Casson η∞ . Usando os valores τ 0 = 0.0108 Pa e η∞ = 0.00276 Pa.s fornecidos na literatura,
obtém-se a variação da viscosidade apresentada na Figura 5, comparada com a do modelo
Carreau-Yasuda dado acima. Observa-se que para γ ≥ 0.3 s-1, quando a reofluificação do
sangue começa a ser mais acentuada, os valores de viscosidade dados pelos dois modelos são
muito próximos. Para valores mais baixos da taxa de corte a viscosidade prevista pelo modelo
de Casson continua a aumentar enquanto a prevista pelo modelo de Carreau tende para um
patamar definido pela viscosidade a taxa de deformação nula η0 .
-4-
10
Carreau-Yasuda
Casson
η(γ) (Ns/m2)
1
0.1
.
0.01
0.001
0.01
0.1
1
100
. 10
γ (1/s)
1000 10000
Fig. 5 Modelo de Casson, variação da viscosidade.
Nessa altura a tensão é próxima da tensão de cedência e o valor da viscosidade deixa de ter
relevância uma vez que, para essa gama de deformações, se tem aproximadamente γ = 0 . Isto
torna-se claro no gráfico da variação da tensão com a taxa de deformação da Figura 6. Para
γ ≤ 0.1 s-1 tem-se τ ≅ 0.01Pa ≈ τ 0 e o modelo de Casson implica comportamento de sólido
indeformável.
1
Carreau
Casson
τ(γ) (N/m2)
0.1
0.01
.
0.001
0.0001
0.01
0.1
.1
γ (1/s)
10
100
Fig. 6 Modelo de Casson, variação da tensão de corte.
A variação da tensão de cedência com o hematócrito é correlacionada pela seguinte expressão
(Merril et al, Biophysical J., 3 (1963) 199- 213; nota: hematócrito em percentagem):
(τ 0 )
1/ 3
= A ( H − H 0 ) (din/cm2), com H 0 = 5 e A = ( 0.008 ± 0.002 )
-5-
Na verdade o valor do hematócrito H 0 acima do qual começa a haver tensão de cedência
pode variar entre H 0 = 1.3 − 6.5 . Nota 1 din/cm2 = 0.1 Pa (Pa=N/m2.). Para H = 45 e
H 0 = 5 , esta expressão dá uma tensão de cedência de τ 0 = ( 0.008 × 40 ) = 0.033
3
din/cm2 = 0.0033 .Pa = 3.3 mPa. Para um valor normal de hematócrito, H = 45 , a gama de
variação da constante A da correlação conduz a uma variação da tensão de cedência entre
τ 0 = 0.001 Pa e τ 0 = 0.0064 Pa (1 e 6 mPa). A correlação acima pode escrever-se em MKS:
τ 0 = 51.2 (φ − φ0 ) mPa
3
com φ0 = 0.05 . Existem expressões semelhantes a esta na literatura, mas sem utilizar o valor
mínimo do hematócrito abaixo do qual não ocorre tensão de cedência. Por exemplo (Picart et
al., J. Rheol. 42 (1998) 1-12):
τ 0 = 26.87 (φ ) mPa
3
Para φ = 0.45 esta expressão dá τ 0 = 2.4 mPa.
Outra expressão encontrada na literatura (Das et al., Biorheology 37 (2000) 239-258) é:
(τ 0 )
1/ 2
 1 α / 2 
2
= β 
 − 1 din/cm
1
−
φ



com: α = 2.0 e β = 0.3315 para sangue humano; e α = 1.621 e β = 0.627 para sangue de
gato. No caso de sangue humano, para um hematócrito de H = 45 , φ = H /100 = 0.45 , vem
τ 0 = 0.0074 N/m2 = 7.4 mPa.
-6-
ANEXOS
1.
Programa para calcular a viscosidade de corte dos modelos de Carreau-Yasuda e Casson
program GNFVIS
C
C
C
C
PREPARE SHEAR VISCOSITY FOR CARREAU AND CASSON MODELS
in simple shear
OPEN(10,FILE='gnfvis.dat')
C Dados partida para modelo Carreau,
C
vis=visinf+(vis0-visinf)*(1+(al*gam)**a)**((n-1)/a)
AL=3.313
VISINF=0.00345
VIS0=0.056
A=2.0
C Dados partida modelo Casson tau**1/2=tauy**1/2+(Kc*gam)**1/2
TAUY=0.0108
AKC=0.00276
print *,' AN ?'
read(*,*) AN
AN1=AN-1.
C
Gama de texas de corte ...
GAM1=1.E-2
GAM2=1.E4
NGAM=200
gl1=alog10(gam1)
gl2=alog10(gam2)
DGAM=(gl2-gl1)/float(ngam)
GLAM=GL1
DO 10 I=1,NGAM
GAM=10.**(GLAM)
C Modelo Carreau viscosidade e tensao corte
VIS=VISINF+(VIS0-VISINF)*(1.+(AL*GAM)**A)**(AN1/A)
TXY=VIS*GAM
C Modelo Casson: tensao corte e viscosidade
TAUC=(SQRT(TAUY)+SQRT(AKC*GAM))**2
VISC=TAUC/GAM
C Escrever no ficheiro gnfvis.dat
WRITE(10,100) GAM,VIS,TXY,VISC,TAUC
GLAM=GLAM+DGAM
10 CONTINUE
100
FORMAT(20(1PE10.3,3X))
STOP
END
2.
Programa para calcular a viscosidade em função do hematócrito
program GNFVIS2
C
C
C
C
PREPARE SHEAR VISCOSITY FOR BLOOD
in simple shear, FUNCTION OF HEMATOCRIT
OPEN(10,FILE='gnfvis2.dat')
T=310.0
VIS0=1.24E-3
RANGE OF H ...
H1=0.0
H2=0.6
NGAM=200
DH=(H2-H1)/float(ngam)
C
H=H1
DO 10 I=1,NGAM+1
A=0.076*EXP(2.49*H+1107/T*EXP(-1.69*H))
VIS=VIS0*(1.0/(1.-A*H))
WRITE(10,100) H*100,VIS,A
H=H+DH
10 CONTINUE
100
FORMAT(20(1PE10.3,3X))
STOP
END
-7-