Problemas Tensões

PROBLEMA 1
Uma placa rectangular está submetida a duas solicitações (S1 e S2), as quais introduzem
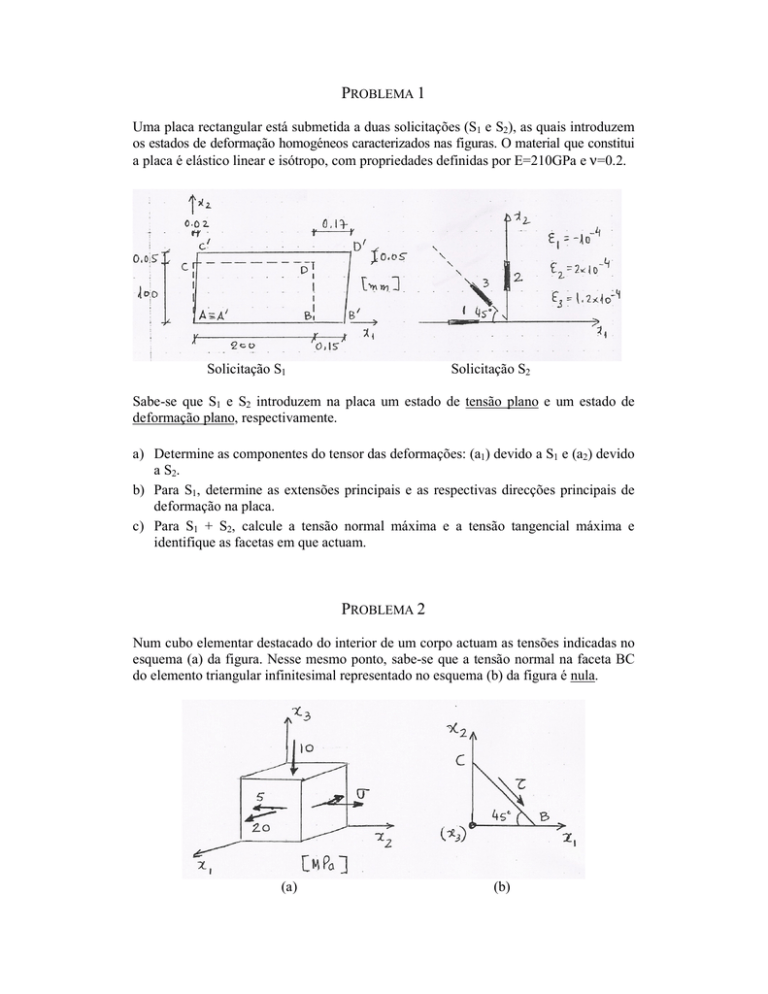
os estados de deformação homogéneos caracterizados nas figuras. O material que constitui
a placa é elástico linear e isótropo, com propriedades definidas por E=210GPa e ν=0.2.
Solicitação S1
Solicitação S2
Sabe-se que S1 e S2 introduzem na placa um estado de tensão plano e um estado de
deformação plano, respectivamente.
a) Determine as componentes do tensor das deformações: (a1) devido a S1 e (a2) devido
a S2.
b) Para S1, determine as extensões principais e as respectivas direcções principais de
deformação na placa.
c) Para S1 + S2, calcule a tensão normal máxima e a tensão tangencial máxima e
identifique as facetas em que actuam.
PROBLEMA 2
Num cubo elementar destacado do interior de um corpo actuam as tensões indicadas no
esquema (a) da figura. Nesse mesmo ponto, sabe-se que a tensão normal na faceta BC
do elemento triangular infinitesimal representado no esquema (b) da figura é nula.
(a)
(b)
a) Defina o tensor das tensões referido ao sistema de eixos (x1, x2, x3).
b) Determine o valor da tensão tangencial τ actuante na faceta BC.
c) Determine o valor da distorção máxima no ponto e indique as direcções das fibras
correspondentes (E=100GPa; ν=0.3).
PROBLEMA 3
Num ponto P de um corpo homogéneo, isotrópico e de comportamento elástico linear
(E=20GPa; ν=0.2), mediram-se as seguintes extensões segundo as direcções indicadas
na figura, as quais estão todas contidas no mesmo plano (estado duplo de deformação
nesse plano).
ε a = 1.5x10 −4
ε b = −3x10 − 4
ε c = 2x10 − 4
a) Calcule as componentes do tensor das tensões no ponto considerado.
Devido à actuação de uma outra solicitação, conhecem-se as componentes do tensor das
tensões correspondentes também a um estado plano de deformação, quando referidas aos
eixos 1’ e 2’:
′ = 9 MPa ; σ ′22 = − 1MPa ; σ 12
′ = −4 MPa .
σ11
b) Para esta segunda solicitação, determine as orientações das normais às facetas para
as quais as componentes normal e tangencial do vector das tensões têm o mesmo
valor absoluto.
c) Para o ponto considerado e para o estado de tensão provocado pela actuação
simultânea das duas solicitações, determine as tensões principais e a orientação das
facetas onde elas actuam.
PROBLEMA 4
Numa placa constituída por um material elástico linear isotrópico, submetida a uma
determinada acção, é conhecido o campo de deslocamentos
(
)
u 1 = x12 − 2 x1 x 2 x10 −3
u 2 = 0.5x10 −3 x 22 + 5
u 3 = 10
−3
(ui e xj em cm)
x3
a) Determine as componentes dos tensores das rotações e das deformações num ponto
de coordenadas (1.5; 1.0; 1.0).
b) Determine entre que direcções ocorre a máxima distorção nesse ponto e qual o seu valor.
c) Sabendo que, no referido ponto, a tensão normal máxima vale 58.33MPa e a tensão
tangencial máxima vale 25MPa, determine o valor do módulo de elasticidade e do
coeficiente de Poisson do material da placa.
PROBLEMA 5
Devido a uma dada solicitação (S1), introduz-se na placa ABCD representada na figura
o seguinte campo de tensões:
σ11 = 2 x 1 x 2
σ12 = − x 12 x 2
σ 22 = x 12 x 2
(MPa )
(MPa )
(MPa )
σ13 = σ 23 = σ 33 = 0
(x1, x2 em cm)
a) Calcule as forças que é necessário aplicar no interior e na fronteira do corpo para
equilibrar o campo de tensões indicado.
Devido à actuação de uma outra solicitação (S2) mediram-se no centro da placa (ponto P)
as seguintes extensões segundo as direcções a, b, e c indicadas na figura:
ε a = 16 x10 −6 ; ε b = 9 x10 −6 ; ε c = 17 x10 −6
Além disso, sabe-se também que a este estado de deformação corresponde um estado
duplo de tensão (a tensão principal nula é segundo a direcção 3).
Para a resolução das alíneas seguintes considere (i) a actuação simultânea das solicitações S1 e
S2 e (ii) o material com um comportamento elástico linear (E=100GPa; ν=0.2).
b) Calcule as componentes principais de tensão no ponto P e indique a orientação das
correspondentes direcções principais.
c) Calcule a extensão volumétrica sofrida por um elemento de volume centrado em P.
PROBLEMA 6
A placa rectangular ABCD, com dimensões 375x250 cm, representada na figura deformou-se
passando a ocupar a posição A´,B´,C´,D´.
Sabendo que (i) o estado de deformação é plano e (ii) o material tem um comportamento
elástico linear isotrópico (E=20GPa; ν=0.25):
a) Calcule as componentes dos tensores das deformações e das rotações referidas ao
sistema de eixos (x1, x2).
b) Determine a extensão da diagonal AC e o ângulo que duas fibras inicialmente alinhadas
com as direcções (x´1, x´2) fazem entre si após a deformação.
c) Determine a variação de temperatura necessária para anular a variação de volume
sofrida pela placa (α=10−5 / ºC).
d) Uma segunda solicitação provocou um estado de tensão plano cujas componentes,
referidas ao sistema (x´1, x´2, x3), valem:
′ = 100 MPa ; σ ′22 = 50 MPa ; σ12
′ = 25 MPa .
σ11
Para a actuação simultânea das duas solicitações, determine:
d1) As componentes do tensor das tensões referidas ao sistema de eixos (x1, x2, x3).
d2) As tensões normal e tangencial máximas, indicando a orientação das facetas nas
quais actuam.