Resposta dos Dispositivos Básicos R, L e C em CA

Centro Federal de Educação
C
ç Tecnológica
g de Santa
S
C
Catarina
Departamento de Eletrônica
Retificadores
Resposta dos Dispositivos Básicos
R, L e C em CA
Prof. Clóvis Antônio Petry.
Florianópolis, agosto de 2007.
Bibliografia para esta aula
Capítulo 14
14:: Os Dispositivos Básicos e os Fasores
1. A derivada;
2. Resposta de R, L e C em CA.
www.cefetsc.edu.br/~petry
Nesta aula
Seqüência
q
de conteúdos:
conteúdos:
1. Revisão;
2. A derivada;
3. Resposta do resistor (R) em CA.
Expressão geral de sinais senoidais
Forma de onda senoidal:
Am ⋅ sen (α )
• Am = valor
l de
d pico;
i
• α = ângulo.
ângulo
O ângulo pode ser dado por:
α = ω ⋅t
Assim:
i ( t ) = I p ⋅ sen (ω ⋅ t )
i (ωt ) = I p ⋅ sen (ωt )
t variando
i d
ωt variando
i d
i (α ) = I p ⋅ sen (α )
α variando
Relações de fase
Forma de onda senoidal:
Am ⋅ sen (ωt ± θ )
• Am = valor de ppico;;
• ω = freqüência angular;
• t = tempo;
• θ = ângulo de deslocamento.
Am ⋅ sen (ωt − θ )
Atraso (θ negativo)
Adiantamento (θ positivo)
Am ⋅ sen (ωt + θ )
Relações de fase
cos (α ) = sen (α + 90
)
sen (α ) = cos (α − 90 )
o
o
Valor médio
t2
f med
Emed
1
=
2π
Emed
Emed
1
= ∫ f ( t ) ⋅ dt
T t1
2π
∫E
m
⋅ sen (α ) ⋅ dα
o
2π
Em
=
⎡⎣ −cos (α ) ⎦⎤ 0
2π
Em
=
⎡⎣ −cos ( 2π ) + cos ( o ) ⎤⎦
2π
Emed = 0
Valor eficaz
t2
f RMS
ERMS
1
=
2π
1
2
=
f ( t ) ⋅ dt
∫
T t1
2π
∫ (E
m
2
⋅ sen (α ) ) ⋅ dα
o
ERMS =
Em
2
A derivada
A derivada de uma senóide é uma co-senóide
co-senóide.
A derivada
A derivada de uma senóide tem o mesmo período e a mesma
Freqüência que a função original.
A derivada
Efeito da freqüência:
A derivada
Para uma tensão senoidal:
e ( t ) = Em ⋅ sen (ωt ± θ )
A li
Aplicando
d ad
derivada:
i d
d (e (t ))
dt
d (e (t ))
dt
d (e (t ))
dt
=
d ( Em ⋅ sen (ωt ± θ ) )
dt
= ω ⋅ Em ⋅ cos (ωt ± θ )
= 2π ⋅ f ⋅ Em ⋅ cos (ωt ± θ )
Resposta do resistor em CA
Para uma dada tensão:
v ( t ) = Vm ⋅ sen (ωt )
i (t ) =
i (t ) =
v (t )
R
Lei de Ohm
v (t )
R
=
Vm ⋅ sen (ωt )
R
Vm
Im =
R
i ( t ) = I m ⋅ sen (ωt )
Resposta do resistor em CA
No caso de um dispositivo
p
p
puramente resistivo,, a tensão e a corrente
no dispositivo estão em fase, sendo a relação entre os seus valores de
pico dada pela lei de ohm.
Resposta do resistor em CA
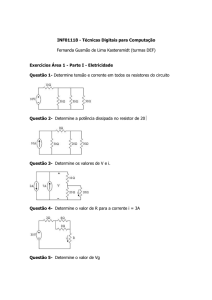
Exercício: Considere que o resistor do circuito abaixo esteja submetido
à tensão com forma de onda senoidal conforme a figura. Determine:
a) Esboce a forma de onda da corrente no resistor;
b) Determine a corrente de pico;
c)) Determine
D t
i a corrente
t média
édi no resistor;
i t
d) Determine a corrente eficaz no circuito.
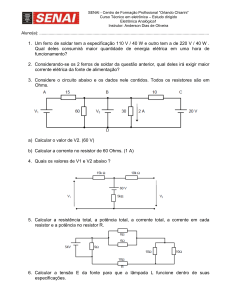
Resposta do resistor em CA
Exercício: Considere que o resistor do circuito abaixo esteja submetido
à tensão com forma de onda senoidal conforme a figura. Determine:
a) Esboce a forma de onda da corrente no resistor;
b) Determine a corrente de pico;
c)) Determine
D t
i a corrente
t média
édi no resistor;
i t
d) Determine a corrente eficaz no circuito.
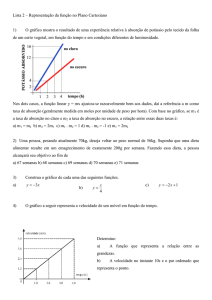
Resposta do resistor em CA
Exercício: Considere que um resistor esteja submetido às formas de onda
de tensão das figuras abaixo. Determine:
a) Esboce a forma de onda da corrente no resistor;
b) Determine a corrente de pico máxima positiva e negativa em R;
c)) Determine
D t
i a corrente
t média
édi no resistor;
i t
d) Determine a corrente eficaz no circuito.
Na próxima aula
Capítulo 14
14:: Os Dispositivos Básicos e os Fasores
1. Resposta de R, L e C em CA.
www.cefetsc.edu.br/~petry