np - sisne.org

Probabilidade e Estatística I – Antonio Roque – Aula 24
Aproximação da Distribuição Binomial pela Distribuição Normal
Uma das utilidades da distribuição normal é que ela pode ser usada para
fornecer aproximações para algumas distribuições de probabilidade
discretas. Vamos considerar aqui a aproximação de uma distribuição
binomial por uma distribuição normal.
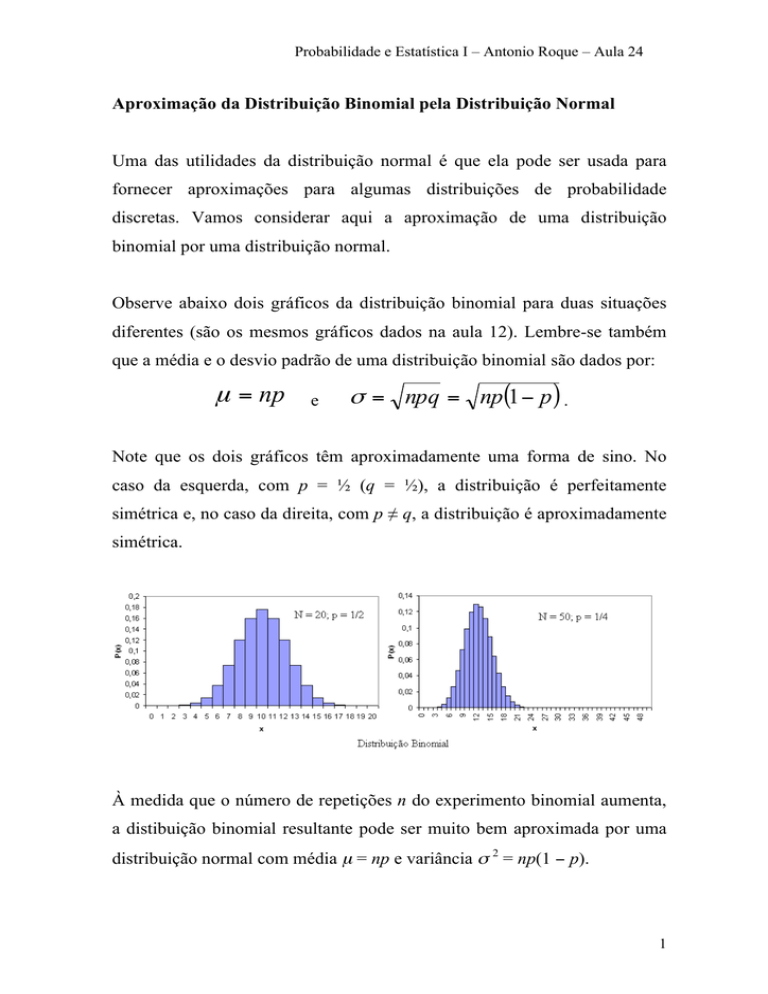
Observe abaixo dois gráficos da distribuição binomial para duas situações
diferentes (são os mesmos gráficos dados na aula 12). Lembre-se também
que a média e o desvio padrão de uma distribuição binomial são dados por:
µ = np
e
σ = npq = np(1 − p ) .
Note que os dois gráficos têm aproximadamente uma forma de sino. No
caso da esquerda, com p = ½ (q = ½), a distribuição é perfeitamente
simétrica e, no caso da direita, com p ≠ q, a distribuição é aproximadamente
simétrica.
À medida que o número de repetições n do experimento binomial aumenta,
a distibuição binomial resultante pode ser muito bem aproximada por uma
distribuição normal com média µ = np e variância σ 2 = np(1 − p).
1
Probabilidade e Estatística I – Antonio Roque – Aula 24
Esta é uma observação empírica (observe os gráficos acima ou gere novos
gráficos para distribuições binomiais com n grande). Também podemos ver
empiricamente que, quanto mais próximo o valor de p for de 0 ou 1, maior
terá que ser o valor de n para que a aproximação fique boa.
A justificativa matemática para a observação empírica de que quanto maior
é o n de uma distribuição binomial, melhor ela pode ser aproximada por
uma distribuição normal com média µ = np e desvio padrão σ = np(1 − p)
é dada por um teorema muito importante em estatística, chamado de
teorema central do limite, e que será visto mais tarde.
Uma das conseqüências do teorema central do limite é a seguinte:
Se uma distribuição binomial satisfizer as condições,
np ≥ 5 e n(1 – p) ≥ 5,
então ela pode ser aproximada por uma distribuição normal com média e
desvio padrão dados por:
µ = np e σ = np(1 − p) .
Exemplo:
Seja um experimento binomial com p = ¼ e q = ¾. Se o experimento for
repetido n = 30 vezes, qual a probabilidade de que haja 9 sucessos?
Pela fórmula da distribuição binomial, a probabilidade pedida é,
P(9 | 30, p = 0,25) =
30!
(0,25)9 (0,75)21 = 0,1298.
9!21!
2
Probabilidade e Estatística I – Antonio Roque – Aula 24
Vejamos agora o que uma distribuição normal com média µ = np = 7,5 e
desvio padrão σ = npq = 2,37 nos dá. Sabemos que ela deve fornecer uma
boa aproximação para o valor calculado acima, pois np = 30.0,25 = 7,5 > 5 e
nq = 30.0,75 = 22,5 > 5.
No entanto, temos um problema: a distribuição normal é uma distribuição
contínua, de maneira que não se define o valor de p(x = 9). A convenção
neste caso é calcular o valor de p(x = 9) como p(8,5 ≤ x ≤ 9,5). Isto é
chamado de correção de continuidade (veja abaixo).
A distribuição binomial é discreta. Então, a probabilidade de x = 9 pode ser
vista como a área de um retângulo centrado em 9 e com largura de 1
unidade. Esta área pode ser aproximada pela área abaixo da função contínua
da distribuição normal entre 8,5 e 9,5.
Para calcular a área entre 8,5 e 9,5, devemos transformar a distribuição
normal acima para a distribuição normal padrão e obter a área entre os
escores-z associados a 8,5 e 9,5, respectivamente. Esses escores-z valem:
z1 =
8,5 − 7,5
9,5 − 7,5
= 0,42 e z 2 =
= 0,84.
2,37
2,37
3
Probabilidade e Estatística I – Antonio Roque – Aula 24
Portanto, a área desejada vale 0,2995 – 0,1628 = 0,1367. Este valor é uma
aproximação razoável para 0,1298. Se o valor de n fosse maior do que 30
(tente em casa para n = 40 e 50), teríamos uma aproximação ainda melhor.
Em geral, se y for uma variável que satisfaça a uma distribuição binomial
com parâmetros n e p, e x for uma variável que satisfaça a uma distribuição
normal com parâmetros µ = np e σ = np(1 − p) tais que np ≥ 5 e n(1 – p) ≥
5, então, para inteiros a e b com a < b, pode-se usar a aproximação:
1
1 ⎞
⎛
P(a ≤ y ≤ b ) ≈ P⎜ a − ≤ x ≤ b + ⎟ .
2
2 ⎠
⎝
Os fatores ½ que aparecem na fórmula acima são devidos à correção de
continuidade.
O exemplo dado deve ter deixado claro que a fórmula acima não é exata,
mas constitui uma aproximação. Ela deve ser usada para o cálculo de uma
probabilidade binomial apenas quando não se tiver à disposição um
computador ou uma tabela conveniente para a distribuição binomial (por
exemplo, quando n for muito grande).
Nas aulas anteriores, vimos que uma distribuição binomial com parâmetros
n e p pode ser aproximada por uma distribuição de Poisson com parâmetro
µ = np quando n for grande e p for pequeno. Isto sugere que uma
distribuição de Poisson também pode ser aproximada por uma distribuição
normal. Observe, por exemplo, os gráficos da distribuição de Poisson a
seguir, retirados da aula 12:
4
Probabilidade e Estatística I – Antonio Roque – Aula 24
À medida que µ cresce, a forma da distribuição de Poisson se aproxima da
forma típica de sino da distribuição normal. Isto também é uma
conseqüência do teorema central do limite.
Para as aplicações práticas, a aproximação de uma distribuição de Poisson
por uma distribuição normal é razoável para µ ≥ 20.
5