Aula 06 | Geometria plana

AULA
ÂNGULOS EM RETAS PARALELAS
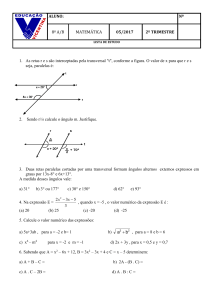
1. Na figura abaixo as retas m e n são paralelas. Os ângulos de medidas x e 40º são:
a) congruentes, pois são colaterais internos.
b) congruentes, pois são correspondentes.
c) congruentes, pois são alternos internos.
d) suplementares, pois são colaterais internos.
e) suplementares, pois são correspondentes.
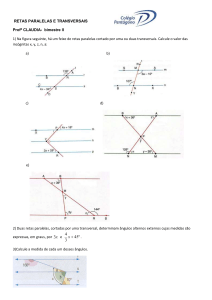
2. Na figura abaixo as retas m e n são paralelas. A diferença entre as medidas dos ângulos indicados por n e m é
igual a:
a) 5º
b) 10º
c) 12º
d) 15º
e) 18º
3. Se duas retas paralelas são cortadas por uma transversal, então a afirmativa falsa é:
a) Os ângulos colaterais internos são congruentes.
b) Os ângulos correspondentes são congruentes.
c) Os ângulos alternos internos são congruentes.
d) Os ângulos alternos externos são congruentes.
e) Os ângulos opostos pelo vértice são congruentes.
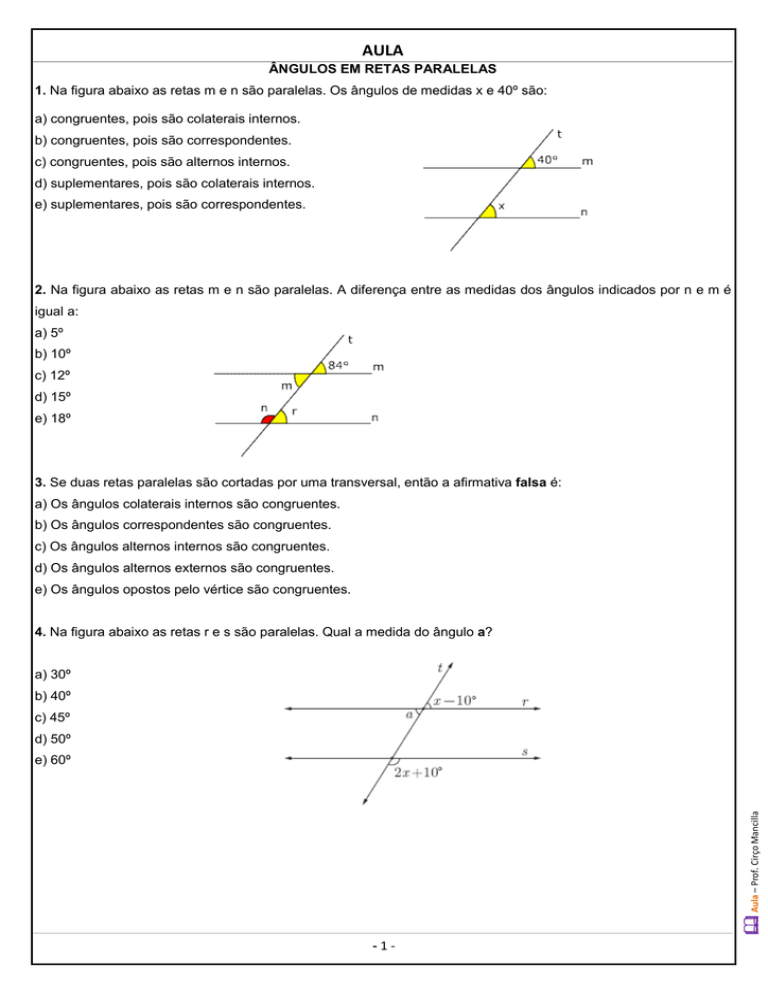
4. Na figura abaixo as retas r e s são paralelas. Qual a medida do ângulo a?
a) 30º
b) 40º
c) 45º
d) 50º
 Aula – Prof. Cirço Mancilla
e) 60º
-1-
AULA
5. Na figura abaixo há duas retas paralelas. Nestas condições, a medida de θ é:
a) 30°
b) 40°
c) 45°
d) 50°
e) 60°
6. Duas paralelas cortadas por uma transversal formam ângulos colaterais internos em que a medida de um deles é
a quarta parte da medida do outro. Quanto mede cada ângulo obtuso formado pelas paralelas com a transversal?
a) 95º
b) 108º
c) 120º
d) 135º
e) 144º
7. Duas retas paralelas cortadas por uma transversal, determinam dois ângulos colaterais internos, em que a
medida de um deles é o triplo da medida do outro. A diferença entre as medidas dos ângulos obtuso e agudo é
igual a:
a) 45º
b) 60º
c) 75º
d) 80º
e) 90º
8. Uma reta transversal corta duas paralelas formando ângulos correspondentes cujas medidas são expressas
por (5x – 48º) e (3x + 12º). A medida de cada ângulo agudo formado é igual a:
a) 83º
b) 78º
c) 72º
d) 65º
 Aula – Prof. Cirço Mancilla
e) 54º
-2-
AULA
9. A soma dos quatro ângulos agudos formados por duas retas paralelas cortadas por uma reta transversal é igual
o
a 80 . Nestas condições, podemos concluir que cada ângulo obtuso mede:
a) 150º
b) 155º
c) 160º
d) 165º
e) 170º
10. Na figura abaixo as duas retas são paralelas. Conclui-se que x+y é igual a:
a) 180o
b) 230o
c) 250o
d) 280o
e) 300o
11. Duas retas paralelas, cortadas por uma transversal, determinam dois ângulos colaterais internos em que a
medida de um deles é o triplo da medida do outro. Faça uma figura representativa dessa situação e determine as
medidas dos oito ângulos formados entre as paralelas e a transversal.
 Aula – Prof. Cirço Mancilla
12. Determine as medidas de x e y, em grau, para cada caso. Considere r // s.
-3-
AULA
13. Na figura, r e s são retas paralelas, e t e u são retas transversais. Determine o valor dos ângulos a, b, c e d
B=
14. Duas retas paralelas cortadas por uma transversal determinam dois ângulos alternos externos cujas medidas
são
3x
+ 15º e 135º. Qual é o valor de x ?
2
15. (CARLOS CHAGAS-SP) Na figura abaixo tem-se r//s; t e u são transversais. O valor de x + y é:
a)
b)
c)
d)
e)
100°
120°
130°
140°
150°
16. (UF-ES) Uma transversal intercepta duas paralelas formando ângulos alternos internos expressos em graus
por (5x + 8) e (7x – 12). A soma das medidas desses ângulos é:
a) 40°
b) 58°
c) 80°
d) 116°
e) 150°
17. As retas t e s são paralelas. A medida do ângulo x, em graus, é:
 Aula – Prof. Cirço Mancilla
a) 30
b) 40
c) 50
d) 60
e) 70
-4-
AULA
18. Na figura abaixo, as circunferências de centros A e B têm raios 9 cm e 6 cm,respectivamente, e a distância
entre os centros é 25 cm. A reta t é uma tangente interior às circunferências nos pontos C e D. Calcule, em
centímetros, a medida do segmento CD
19. Por um ponto A de uma circunferência, traça-se o segmento AH perpendicular a um diâmetro BC , conforme a
figura abaixo. Se o ponto H determina no diâmetro segmentos de 4 cm e 9 cm, calcule a medida x do segmento
AH , a medida y da corda AB e a medida z da corda AC .
20. (FUVEST) Na figura, a circunferência de centro O é tangente à reta CD no ponto D, o qual pertence à reta
AO . Além disso, A e B são pontos da circunferência, AB = 6 3 e BC = 2 3 . Nessas, condições, determie:
a) A medida do segmento CD ;
b) O raio da circunferência;
c) A área do triângulo AOB;
 Aula – Prof. Cirço Mancilla
d) A área da região hachurada na figura.
-5-
AULA
21. (UNIFOR) Na figura a seguir, as retas r e s são paralelas entre si e AB = 2cm.
A medida do segmento AC ,em centímetros, é:
a) 4
b) 2 3
c) 3
d) 2 2
e) 2
22. Na figura a seguir, AB = AC, AD é bissetriz do ângulo BÂC e AE é bissetriz do ângulo BÂD.
A medida do ângulo x, em graus, é
a) 110º.
b) 112º.
c) 116º.
d) 120º.
e) 122º.
23. Num triângulo ABC, o ângulo interno de vértice A mede 60°. O maior ângulo formado pelas bissetrizes dos
ângulos internos de vértices B e C mede:
a) 45º.
b) 60º.
 Aula – Prof. Cirço Mancilla
c) 90º.
d) 120º.
e) 150º.
-6-
AULA
24. Na figura, AB é paralelo a CD . O valor de sen x é:
2
2
3
b)
2
1
c)
2
d) 1
e) 0
a)
25. As retas r e s da figura são paralelas cortadas pela transversal t. Se o ângulo B é o triplo de A, então B - A
vale:
a) 90º.
b) 85º.
c) 80º.
d) 75º
e) 60º.
26. (UNIRIO) As retas r 1 e r 2 ‚ são paralelas. O valor do ângulo α , apresentado na figura a seguir, é:
a) 40º
b) 45º
c) 50º
d) 65º
 Aula – Prof. Cirço Mancilla
e) 130º
-7-
AULA
27. Sabendo que as retas r e s da figura ao lado são paralelas, o valor, em graus, de α - β é:
a) 12º.
b) 15º.
c) 20º.
d) 30º.
e) 40º.
28. Um triângulo equilátero RSV foi construído tendo como base um lado de um quadrado RSTU, como na figura
abaixo.
Como o triângulo é equilátero, todos os seus lados são iguais e todos seus ângulos internos medem 60º. Os lados
do quadrado tem a mesma medida do lado do triângulo. Com base nessas informações, determine o valor do
ângulo α .
01. Um giro de um quarto de volta corresponde a um ângulo de 45º.
02. Um giro de meia-volta corresponde a um ângulo de 180º.
04. Retas perpendiculares se cruzam a um ângulo de 90º..
08. Um giro de uma volta e meia corresponde a 450º..
16. Retas paralelas se interceptam formando um ângulo de 0º.
-8-
 Aula – Prof. Cirço Mancilla
29. Assinale a alternativa que representa a soma das sentenças corretas:
AULA
a) 15
b) 23
c) 7
d) 6
e) 14
30. Na figura abaixo, as retas r e s são paralelas. Calcule a.
 Aula – Prof. Cirço Mancilla
 excede o ângulo A
 e C
 em
31. Num triângulo ABC, o ângulo obtuso formado pelas bissetrizes dos ângulos B
.
76°. Determine A
-9-
AULA
GABARITO
1. Alternativa B
2. n – m = 12º
3. Alternativa A
4. a = 50º
5. θ = 50º
6. α = 144º
7. β - α = 90º
8. α = 78º
9. α = 160º
10. x + y = 230º
11. quatro ângulos: α = 135º e quatro ângulos: β = 45º
12.
a) x = 45º e y = 40º
b) x = 130º e y = 88º
c) x = 50º e y = 130º
d) x = 26º e y = 42º
13. a = 70º
b = 70º
c = 40º
d = 140º
14. x = 80º
15. x + y = 130º
16. A soma é 116º
17. x = 70º
18. CD = FB = 20 cm
19. x = 6 cm
y = 2 13 cm
z = 3 13 cm
20.
a) CD = 4 3 cm
b) r = 6 cm
c) A = 9 3 cm2
d) 12π - 9 3 cm2
21. AC = 2 3 cm
22. x = 116º
23. α = 120º
1
2
 Aula – Prof. Cirço Mancilla
24. sen 30º =
25. B - A = 90º
26. α = 40º
27. α - β = 30º
28. α = 75º
29. soma: 02 + 04 = 06
- 10 -
AULA
30. a = 52º
 Aula – Prof. Cirço Mancilla
31. x = 28º
- 11 -