IV Tensão e Equilíbrio

TENSÃO E EQUILÍBRIO
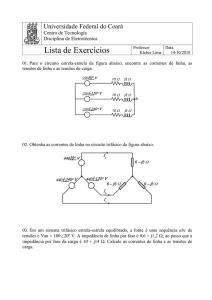
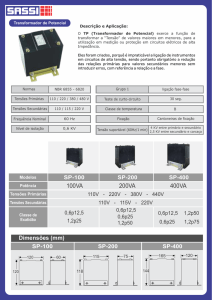
----------------------------------Prof. Dr. Julio
Almeida
ELASTICIDADE LINEAR
CLÁSSICA
1
TENSÃO E EQUILÍBRIO
Quando uma estrutura é submetida à cargas
externas, forças internas são induzidas no interior
do elemento em análise. Tais forças são, ainda,
distribuídas continuamente ao longo de todo o
sólido.
Existem duas categorias de forças internas na
mecânica do contínuo: forças de corpo
(eletromagnéticas, gravitacionais) e forças de
superfície (forças de contato).
2
1
FORÇAS DE CORPO
As forças de corpo são proporcionais à massa do
corpo e normalmente são definidas como forças
por unidade de volume, podendo ser descritas na
forma:
r
r
FR = ∫ F ( x) dV
V
3
FORÇAS DE SUPERFÍCIE
As forças de superfície são forças por unidade de
área, sendo que a resultante das mesmas ao longo
de uma superfície S é função do chamado vetor
tração (Tn(x)).
r
rn
FS = ∫ T ( x) dS
S
4
2
VETOR TRAÇÃO
P3
P2
∆F
n
∆A
p
P1
(Sectioned Body)
(Externally Loaded Body)
∆F = força de superfície resultante atuante em ∆A
5
VETOR TRAÇÃO
∆F
n
O vetor tração ou tensão é
definido por:
∆A
(Sectioned Body)
rn
∆F
T ( x ,n ) = lim
∆A→0 ∆A
notar que o vetor tração depende da localização
espacial e do vetor unitário normal à superfície
em estudo!!
6
3
VETOR TRAÇÃO
Supondo agora o caso especial no qual ∆A
coincida com cada um dos três planos
coordenados e tenha os vetores unitários
normais direcionados no sentido positivo dos
eixos coordenados, na forma:
7
VETOR TRAÇÃO
as componentes normais necessitam de apenas um
subscrito, sempre normal à superfície em análise;
as componentes tangenciais necessitam de dois
subscritos, sendo que o primeiro representa o plano
de ação e o segundo representa a direção da
8
tensão.
4
TENSOR TENSÃO DE CAUCHY
Supondo agora um tetraedro
(tetraedro de Cauchy) na forma:
infinitesimal
y
n
Tn
x
z
9
TENSORES DE TENSÃO:
CAUCHY x PIOLA-KIRCHOFF
Pela teoria das pequenas deformações, o tensor
tensão e o vetor tração podem ser aplicados de
forma indiferente à configuração original ou à
configuração deformada do elemento
Por outro lado, para a teoria das grandes
deformações, tal condição não é válida sendo a
configuração original a frequentemente utilizada na
formulação do problema.
10
5
TRANSFORMAÇÃO DE TENSÃO
Por se tratar de um tensor de segunda ordem,
valem
as
mesmas
regras
anteriormente
estabelecidas para a transformação de eixos.
Assim:
σ ij ' = Qip Q jqσ pq
Qij = cos( xi ' , x j )
l1
m1
n1
Qij = l2
m2
n2
l3
m3
n3
11
TRANSFORMAÇÃO DE TENSÃO
resultando em:
σ ij ' = Qip Q jqσ pq
σ 11 ' σ 12 ' σ 13 ' l1 m1 n1 σ 11 σ 12 σ 13 l1 m1 n1
σ 21 ' σ 22 ' σ 23 ' = l2 m2 n2 σ 21 σ 22 σ 23 l2 m2 n2
σ 31 ' σ 32 ' σ 33 ' l3 m3 n3 σ 31 σ 32 σ 33 l3 m3 n3
T
12
6
TRANSFORMAÇÃO DE TENSÃO
resultando em:
σ x ' = σ x l12 + σ y m12 + σ z n12 + 2(τ xy l1m1 + τ yz m1n1 + τ zx n1l1 )
σ y ' = σ x l2 2 + σ y m2 2 + σ z n2 2 + 2(τ xy l2 m2 + τ yz m2 n2 + τ zx n2l2 )
σ z ' = σ x l3 2 + σ y m3 2 + σ z n3 2 + 2(τ xy l3 m3 + τ yz m3n3 + τ zx n3l3 )
τ xy ' = σ xl1l2 + σ y m1m2 + σ z n1n2 + τ xy (l1m2 + m1l2 ) + τ yz (m1n2 + n1m2 ) + τ zx (n1l2 + l1n2 )
τ yz ' = σ xl2l3 + σ y m2 m3 + σ z n2 n3 + τ xy (l2 m3 + m2l3 ) + τ yz (m2 n3 + n2 m3 ) + τ zx (n2l3 + l2 n3 )
τ zx ' = σ xl3l1 + σ y m3m1 + σ z n3n1 + τ xy (l3m1 + m3l1 ) + τ yz (m3 n1 + n3m1 ) + τ zx (n3l1 + l3 n1 )
13
TRANSFORMAÇÃO DE TENSÃO
Particularizando para 2D:
l1
m1
n1
Qij = l2
m2
n2
l3
m3
n3
cosθ
Qij = − senθ
0
senθ
0
cosθ
0
0
1
14
7
EXEMPLO 01
Dado o tensor de tensão [σ
σ] atuante num ponto P,
determinar o vetor tensão passando por P e
simultaneamente paralelo ao plano ABC, sendo A
(4,0,0), B(0,2,0) e C(0,0,6).
7
[σ ] = − 5
0
−5 0
3
1
1
2
15
TENSÕES PRINCIPAIS
Plano no espaço no qual as tensões tangenciais
desaparecem, permanecendo apenas tensões
normais, as quais, nessas circunstâncias, são
designadas por tensões principais.
16
8
TENSÕES PRINCIPAIS
Adaptando-se a equação característica:
[
]
det σ ij − σδ ij = −σ 3 + I1σ 2 − I 2σ + I 3 = 0
e os invariantes:
I1 = σ ii = tr [σ ] = σ 11 + σ 22 + σ 33
I2 =
1
(σ iiσ jj − σ ijσ ji ) = σσ 11 σσ 12 + σσ 22 σσ 23 + σσ 11 σσ 13
2
32
33
31
33
21
22
[ ]
I 3 = det σ ij
17
DECOMPOSIÇÃO DO VETOR TRAÇÃO
N
∆A
n
Tn
S
N = componente normal
S = componente tangencial
18
9
DECOMPOSIÇÃO DO VETOR TRAÇÃO
S 2 + (N − σ 2 )( N − σ 3 ) ≥ 0
S 2 + (N − σ 3 )( N − σ 1 ) ≥ 0
S 2 + (N − σ 1 )( N − σ 2 ) ≥ 0
S
S 2 + ( N − σ 2 )( N − σ 3 ) = 0
N
σ3
σ2
σ1
S 2 + ( N − σ1 )( N − σ 2 ) = 0
com : S max =
S + ( N − σ 3 )( N − σ1 ) = 0
2
σ1 − σ 3
2
resultados obtidos por Otto Mohr
19
TENSÕES ESFÉRICA E DESVIATÓRIA
O tensor esférico ou hidrostático corresponde ao
caso em que cada tensão normal é igual a (-p) e as
tensões tangenciais correspondentes são nulas.
Esse tensor produz assim apenas mudança de
volume, sem mudança de forma, no corpo em
análise.
1
3
σ hid = σ med = − p = σ ii =
I1
3
20
10
TENSÕES ESFÉRICA E DESVIATÓRIA
O tensor desviatório é aquele responsável pela
mudança de forma, além de ser também o
responsável pela plastificação do material.
σ D = σ ij − σ hid
21
PLANO OCTAÉDRICO E TENSÕES
OCTAÉDRICAS
Suponha agora um plano especial cuja normal faz
ângulos idênticos com os 3 eixos principais:
22
11
PLANO OCTAÉDRICO E TENSÕES
OCTAÉDRICAS
ni = ±
(1,1,1)
3
23
TENSÃO DE MISES
A tensão tangencial octaédrica é diretamente
relacionada com a energia de distorção de
deformação, critério convencionalmente utilizado
como teoria de falha para materiais dúcteis.
Tal critério de falha é também conhecido como
critério de Mises, cuja tensão efetiva vale:
σ '= σ e =
1
2
(σ − σ ) + (σ − σ ) + (σ
2
1
2
2
1
3
−σ3)
2
2
24
12
EXEMPLO 02
Dado o tensor de tensões num ponto genérico,
determinar as tensões principais e suas
correspondentes direções.
3 1 1
[σ ] = 1
0 2
1 2 0
Verificar, ao final, que a transformação do tensor
tensões original resulta nas tensões principais
mediante a matriz de transformação dos cossenos
diretores principais.
25
EQUAÇÕES DE EQUILÍBRIO
Considerando, assim, uma região com uma
distribuição geral de forças de superfície e forças
de corpo na forma:
Tn
S
V
F
σ
ji , j
+ Fi = 0
26
13
EQUAÇÕES DE EQUILÍBRIO
qualquer campo de tensões elástico deve,
obrigatoriamente, atender as relações de equilíbrio
no contexto de garantir o equilíbrio estático.
27
SIMETRIA DAS TENSÕES TANGENCIAIS
Pelo princípio do momentum angular deve-se
garantir que o momento de todas as forças
atuantes em qualquer porção do corpo deva ser
nulo. Mediante tal condição, pode-se demonstrar
que:
σ ij = σ ji
comprovando-se a simetria do tensor tensões.
28
14
EXEMPLO 03
As tensões principais em um ponto P pertencente
a um sólido elástico, referidos a um sistema
cartesiano ortogonal Oxyz, são:
r r
r 50 r
σ 1 = (2i + 2 j + k )
3
r
r 30 r r
σ 2 = (2i − j − 2k ) ( MPa )
3
r
r
20 r
r
σ 3 = − (i − 2 j + 2k )
3
Calcular a tensão correspondente a um plano cuja
normal exterior forma ângulos agudos iguais com
os semi-eixos positivos do triedro Oxyz.
29
EXEMPLO 04
A matriz de tensões nos pontos de um sólido
elástico vale:
− 6( x + y + z )
 4x + 3y

[T] = − 6( x + y + z ) 10( y − z )

y+z
3x
y + z
3 x 
5 z 
com tensões em kgf/mm2 e coordenadas em
metros.
a) Determinar as forças de volume (N/m3)
correspondentes
b) Determinar, em forma matricial, as tensões
esférica e desviadora no ponto P(0,1,-1)
30
15
EXEMPLO 05
Para o caso de cisalhamento
é dada por:
0 τ
σ ij = τ 0
0 0
puro, a matriz tensão
0
0
0
Determine as tensões e direções principais e
defina as tensões normal e cisalhante no plano
octaédrico.
31
BIBLIOGRAFIA DE REFERÊNCIA
Boresi, A. P. & Chong, K. P., Elasticity in Engineering Mechanics,
Prentice Hall, Inc. (2000).
Saad, M. H., Elasticity – Theory, Applications and Numerics, Elsevier
(2005).
Prof. Julio Almeida
32
16