1 Ângulo é a região de um plano concebida pela abertura de

CURSO: ASTRONOMIA APLICADA À NAVEGAÇÃO
PROFESSOR: ALEXANDRE RIBEIRO ANDRADE
MÓDULO 1:
MATEMÁTICA APLICADA NA ASTRONOMIA NÁUTICA
Lista de exercícios 3:
Ângulos e Arcos
Ângulo é a região de um plano concebida
pela abertura de duas semirretas que possuem uma
origem em comum, chamada vértice do ângulo. A
abertura do ângulo é uma propriedade invariante e
é medida em radianos ou graus.
comum e este modo foi o primeiro passo para
medir um ângulo, objeto este que se tornou
importantísimo no contexto científico.
Na verdade, não se sabe quando o homem
começou a medir ângulos, mas se sabe que estes
eram medidos na Mesopotâmia e eram muito bem
conhecidos quando Stonehenge foi construída,
2000 a.C.
Quanto ao conceito de ângulo, temos
algumas definições:
Grécia antiga: "Um ângulo é uma
deflexão ou quebra em uma linha reta".
Euclides: "Um ângulo plano é a inclinação
recíproca de duas retas que num plano têm um
extremo comum e não estão em prolongamento".
Em 1893, H.Schotten resumiu as
definições de ângulo em três tipos:
1. A diferença de direção entre duas retas;
2. A medida de rotação necessária para
trazer um lado de sua posição original
para a posição do outro, permanecendo
entrementes no outro lado do ângulo;
3. A porção do plano contida entre as duas
retas que definem o ângulo.
Em 1634, P.Henrigone definiu ângulo como
um conjunto de pontos, definição esta que tem
sido usada com mais frequência. Neste trabalho,
aparece pela primeira vez o símbolo "<" para
representar ângulo.
Ângulos consecutivos: Dois ângulos são
consecutivos se um dos lados de um deles
coincide com um dos lados do outro ângulo.
O
conceito
de
ângulo
aparece
primeiramente em papiros gregos no estudo de
relações envolvendo elementos de um círculo
junto com o estudo de arcos e cordas. As
propriedades das cordas, como medidas de
ângulos centrais ou inscritas em círculos, eram
conhecidas desde o tempo de Hipócrates e talvez
Eudoxo tenha usado razões e medidas de ângulos
na determinação das dimensões do planeta Terra e
no cálculo de distâncias relativas entre o Sol e a
Terra. Eratóstenes de Cirene (276 a.C.-194 a.C) já
tratava de problemas relacionados com métodos
sistemáticos de uso de ângulos e cordas.
Desde os tempos mais antigos, os povos
vêm olhando para o céu na tentativa de encontrar
respostas para a vida tanto na Terra assim como
entender os corpos celestes que aparecem à nossa
vista. Assim, a Astronomia talvez tenha sido a
primeira ciência a incorporar o estudo de ângulos
como uma aplicação da Matemática.
Na determinação de um calendário ou de
uma hora do dia, havia a necessidade de realizar
contagens
e
medidas
de
distâncias.
Frequentemente, o Sol servia como referência e a
determinação da hora dependia da inclinação do
Sol e da relativa sombra projetada sobre um certo
indicador (relógio de Sol).
Para obter a distância que a Lua estava
acima do horizonte, dever-se-ia calcular uma
distância que nunca poderia ser medida por um ser
humano comum. Para resolver este problema,
esticava-se o braço e se calculava quantos dedos
comportava o espaço entre a Lua e o horizonte ou
então, segurava-se um fio entre as mãos afastadas
do corpo e se media a distância.
Os braços deveriam permanecer bem
esticados para que a resposta fosse a mais fiel
possível. A medida era diferente de uma medida
AÔC e BÔC são consecutivos OC é o lado
comum
1
AÔB e BÔC são consecutivos OB é o lado
comum
circunferência (não importa a medida do raio).
Indicamos o ponto A como uma das interseções
da circunferência com a reta horizontal. Tomamos
um barbante com a mesma medida que o raio OA
da circunferência. Fixamos uma das extremidades
do barbante sobre o ponto A e esticamos o
barbante sobre a circunferência. O ponto B
coincidirá com a outra extremidade do barbante.
Traçamos então o segmento de reta OB, que
representa o outro lado do ângulo AOB. A medida
do ângulo AOB é 1 radiano.
Ângulos adjacentes: Dois ângulos
consecutivos são adjacentes se, não têm pontos
internos comuns.
AÔB e BÔC são ângulos adjacentes.
Consideremos duas retas concorrentes cuja
interseção seja o ponto O. Estas retas determinam
quatro ângulos. Os ângulos que não são adjacentes
são opostos pelo vértice.
Outra unidade é muito utilizada nos
primeiros níveis educacionais é o grau. Ela é
obtida pela divisão da circunferência em 360
partes iguais, obtendo-se assim um ângulo de um
grau, sendo que a notação desta medida usa um
pequeno o colocado como expoente do número,
como 1º.
Acerca de elementos geométricos
relacionados com a Astronomia pouco se conhece.
Sabe-se que Aristarco propôs um sistema que
tinha o Sol como centro pelo menos 1500 antes de
Copérnico, no entanto este material histórico se
perdeu na noite do tempo. O que ficou, do ponto
de vista histórico foi um tratado escrito por volta
de 260 a.C. envolvendo tamanhos e distância do
Sol e da Lua.
A congruência entre ângulos é uma noção
primitiva. Dizemos que dois ângulos são
congruentes se, superpostos um sobre o outro,
todos os seus elementos coincidem.
A divisão do círculo em 360 partes iguais
aparece mais tarde e não existe qualquer razão
científica. Talvez exista uma razão histórica que
justifique a existência de tal número no contexto
de estudos do povo babilônio, que viveu entre
4000 a.C. e 3000 a.C. Este povo realizava muitos
estudos no trato de terrenos pantanosos e
construções de cidades e tinha interesse pela
Astronomia assim como pela sua relação com
conceitos religiosos (eram politeistas) e para
viabilizar tais procedimentos, criaram um sistema
de numeração com base 60 (sistema hexagesimal).
Na figura acima, temos que ABC e DEF
são ângulos congruentes. Usamos a notação
para denotar ângulos congruentes. Dois ângulos
opostos pelo vértice são sempre congruentes.
A unidade de medida de ângulo no
Sistema Internacional é o radiano e o processo
para obter um radiano é o seguinte:
Tomamos um segmento de reta OA. Com um
compasso centrado no ponto O e abertura OA,
traçamos um arco de circunferência AB, sendo
que B deve pertencer ao outro lado do ângulo
AOB. Se o comprimento do arco for igual ao
comprimento do segmento OA, diremos que este
ângulo tem medida igual a 1 radiano (1 rad).
Não se sabe ao certo quais as razões pelas quais,
foi escolhido o número 360 para se dividir a
circunferência, sabe-se apenas que o número 60 é
um dos menores números menores do que 100 que
possui uma grande quantidade de divisores
distintos, a saber: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20,
Uma forma prática de visualizar isto é tomar uma
reta horizontal passando pelo centro de uma
2
30, 60, razão forte pela qual este número tenha
sido adotado.
----A LUA MOSTRA A POSIÇÃO DO SOL
O primeiro astrônomo grego a dividir o
círculo em 360 partes foi Hipsicles (180 a. C.),
seguido pelos caldeus. Por volta de 150 a. C.
encontramos uma generalização de Hiparco para
este procedimento.
Olhe para a Lua a noite ou durante o dia. Se
ela não estiver muito cheia nem toda escura, você vai
poder notar as cúspides, que são aquelas pontas da
parte iluminada do disco lunar, principalmente na
semana que antecede e na que sucede a Lua Nova.
Imagine que o limbo (bordo) iluminado do
disco lunar é um arco indígena, com as cúspides sendo
as extremidades.
Ligue-as por uma linha reta e você terá a
corda. Agora, calcule para onde uma flecha vai, se for
disparada por esse arco.
Dividir um círculo em 6 partes iguais era
algo muito simples para os especialistas daquela
época e é possível que se tenha usado o número
60 para representar 1/6 do total que passou a ser
360.
Outro fato que pode ter influenciado na
escolha do número 360 é que o movimento de
translação da Terra em volta do Sol se realizava
em um período de aproximadamente 360 dias, o
que era uma estimativa razoável para a época.
Hiparco mediu a duração do ano com grande
exatidão ao obter 365,2467 dias, sendo que
atualmente esta medida corresponde a 365,2222
dias.
Tipos de Ângulos
Com relação às suas medidas, os ângulos podem
ser classificados como: reto, agudo, obtuso e raso.
Texto e imagem do livro: BARROS, G. M.
“Astronomia sem mistérios : uma introdução à
astronomia náutica”.
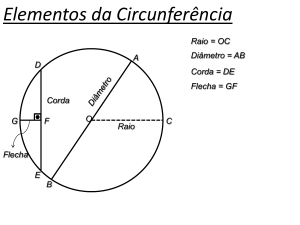
ARCO
É a porção compreendida entre dois pontos (os
extremos) de uma curva. Existem, por exemplo, o arco
de circunferência (também chamado de arco de
círculo), o arco de elipse, etc. O arco que corresponde à
metade
de
uma
circunferência
é
uma
semicircunferência; a quarta parte é um quadrante.
Designa-se como amplitude de um arco (de
circunferência) a medida do ângulo com vértice no
centro da circunferência correspondente e definido
pelos extremos do arco.
Designa-se como corda o segmento de reta
que une os extremos de um arco de circunferência.
Quando dois arcos de circunferência compartilham a
mesma corda (têm os mesmos extremos), diz-se que
são arcos suplementares.
Designa-se como flecha o segmento de reta
perpendicular a uma corda cujas extremidades são o
ponto médio da corda e o ponto correspondente no
arco.
A unidade de medida de arco do Sistema
Internacional de Unidades (SI) é o radiano, mas
existem outras medidas utilizadas pelos técnicos que
são o grau e o grado. Este último não é muito usado.
Radiano: Medida de um arco que tem o
mesmo comprimento que o raio da circunferência na
Em problemas reais, os ângulos nem sempre
possuem medidas associadas a números inteiros, assim
precisamos usar outras unidades menores como
minutos e segundos. A notação para 1 minuto é 1' e a
notação para 1 segundo é 1".
Subdivisões do grau
Assim
1 grau = 1 ângulo reto dividido por 90.
1 minuto = 1 grau dividido por 60.
1 segundo = 1 minuto dividido por 60.
Exemplo: Expressar a medida do ângulo 35º 48' 36"
como fração decimal do grau.
35º48'36" = 35º + 48' + 36" = 35º + (48/60)º +
(36/3600)º = 35º + 0,80º + 0,01º= 35,81º
3
qual estamos medindo o arco. Assim o arco tomado
como unidade tem comprimento igual ao comprimento
do raio ou um radiano, que denotaremos por "1 rad".
Grau: Medida de um arco que corresponde a
1/360 do arco completo da circunferência na qual
estamos medindo o arco.
Grado: É a medida de um arco igual a 1/400
do arco completo da circunferência na qual estamos
medindo o arco.
REFERÊNCIAS BIBLIOGRAFICAS
BARROS, G. M. “Astronomia sem mistérios : uma
introdução à astronomia náutica”. 4ª Ed. - Porto Alegre:
FormaDiagramação, 2009.
http://pessoal.sercomtel.com.br/matematica/fundam/geo
metria/geo-ang.htm#m112b02
http://pt.wikipedia.org/wiki/%C3%82ngulo
Exemplo: Para determinar a medida em
radianos de um arco de comprimento igual a 12 cm, em
uma circunferência de raio medindo 8 cm:
Para converter em grau, basta aplicar uma
regra de três:

Exercícios
1) Use a regra de três para converter ângulos em
graus em radiano:
a)
d)
g)
j)
m)
360º
280º
175º
95º
32º
b) 330º
e) 245º
h) 160º
k) 80º
n) 15º
c) 300º
f) 200º
i) 115º
l) 46º
2) Converta o ângulo fracionário decimal em
minuto e segundos, se possível.
a)
d)
g)
j)
m)
36,34º
280,45º
165,4º
93,1º
321,4º
b) 330,5º
e) 24,5º
h) 160,9º
k) 82,4º
n) 25,6º
c) 3,6º
f) 20,33º
i) 105,76º
l) 48,8º
3) Converta o ângulo em minuto e segundos em
ângulo decimal, se possível.
a)35º 34’ 32”
d)28º 21’ 21”
g)16º 54’02”
j) 91º 57’ 21”
m) 224º 44’ 12”
4)
5)
b) 330º 40’ 12”
e) 23º 59’ 50’
h)183º 44’ 32”
k) 8º 12’ 25”
n) 216º 32’ 17”
c) 13º 33’
f) 2º 22’ 2”
i)11º 11’ 3”
l) 4º 23’ 34”
Escreva os ângulos obtidos do exercício (3) em
radianos.
Em uma circunferência de raio igual a 10, calcular
as medidas dos arcos subtendidos pelos ângulos
dados pelo exercício (3):
4