Circunferência e Círculo II

Elementos da Circunferência
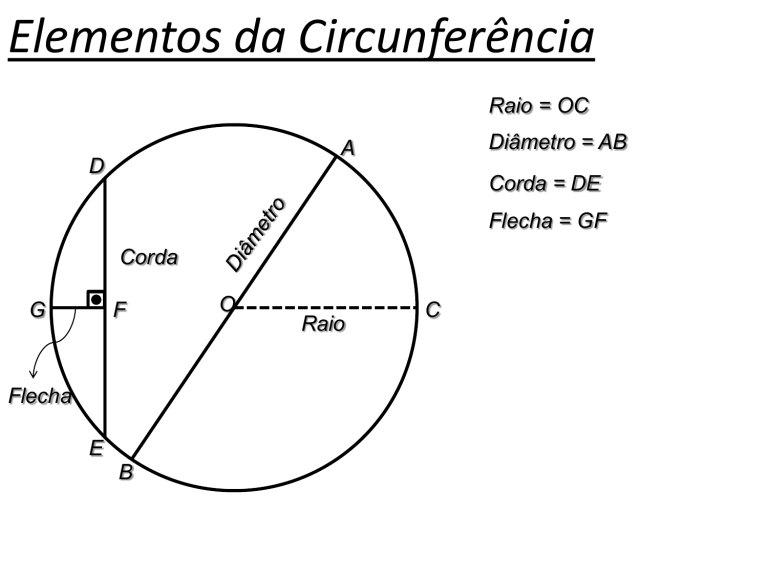
Raio = OC
Diâmetro = AB
A
D
Corda = DE
Flecha = GF
Corda
G
F
Flecha
E
B
O
Raio
C
P
s
s é reta tangente
r é reta secante
Q
PQ = arco
r
O
Comprimento da
Circunferência
Comprimento de um arco de
Circunferência

R
graus :
C  2. .R
2. .R  360

 

radianos :
2. .R  2 rad


  rad
Ângulos na circunferência
Ângulo Central:
A
  arco  AB 

B
Ângulo Inscrito:
A
B


arco  AB 
2
Ângulo de Segmento:
A


B
arco  AB 
2
Ângulo Excêntrico Interior:
A
C


B
D

arco  AB   arco  CD 
2
Ângulo Excêntrico Exterior:
A
C
B

D

arco  AB   arco  CD 
2
Propriedades da Circunferência
P
B
P
Q
A
A e B são pontos de
tangência, então
PA = PB
A e B são extremos do
diâmetro, os pontos P e Q
são pontos da
semicircunferência, que
unidos aos extremos do
diâmetro determinam
ângulos retos
P
A
B
Q
Teorema de Pitot:
B
2
1
C
A
3
4
D

1
3

2

4
Teorema de Ptolomeu:
d1
4
A
B
1
A
B
C
C
3

2
d2
D

D
    180
Ângulos opostos de
quadriláteros inscritíveis são
suplementares
Relações Métricas na Circunferência
D
B
A
A
B
E
P
C
D
C
(AE).(EB) = (CE).(ED)
(PA).(PB) = (PC).(PD)
A
P
C
D
(PA)² = (PC).(PD)
Círculo
R
A   .R²
Setor Circular
360   .R



A
setor

2
R

R
2. .R   .R


A
setor

2
Segmento Circular
Asegmento  Asetor  Atriângulo
R

R
1

 Atriângulo  2 .R.R.sena

R ².sena
A
triângulo 

2
Coroa Circular
R
r
 Acoroa   .R ²   .r ²

 Acoroa   .( R ²  r ²)
A
 coroa   .( R  r ).( R  r )