MOSFET: Revisão
EIII
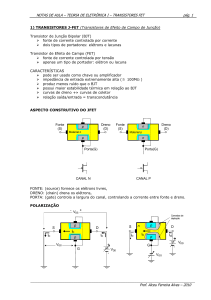
Contacto de dreno/fonte
(drain/source)
Contacto da Porta
(gate)
Polisilício
Contacto de fonte/dreno
(source/drain)
Contacto de
substrato
SiO2
Metalização
Tox
n+
p-
Oxido fino
n+
Lmin
p+
LD
Substrato
• Não há diferença física entre o dreno e a fonte. A
menor tensão dos dois define a fonte.
•O polisilício permite o fabrico de MOSFETs com o
canal bem alinhado com a porta (processo autoalinhado).
Lmin< 90nm
Tox< 2nm
FEUP
VGT
1
MOSFET
MOSFET: Revisão
EIII
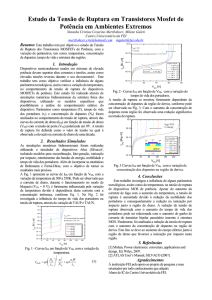
G
• Símbolos
D/S
S/D
n+
p-
A corrente de porta é diminuta
(~10-17A), no entanto as capacidades
parasitas acoplam o sinal da porta aos
sinais de dreno e/ou fonte.
FEUP
n+
B
O substrato (B) normalmente é ligado à tensão mais baixa do
circuito. Desta forma, o transístor estará rodeado de junções
inversamente polarizadas que o isolam electricamente de outros
MOSs, prevenindo que surjam correntes entre transístores através
do substrato .
VGT
MOSFET
2
1
EIII
MOSFET: Modos de operação básicos
1. Região de acumulação:
Vg<<0
- Com Vg<<0 há acumulação de
lacunas na região de substrato por
baixo do oxido fino da porta.
- Na região de acumulação forma-se
um canal com densidade de lacunas
p+.
+ + + +
n+
n+
p-
- Mesmo que as tensões de dreno
e/ou fonte cresçam, não há condução
possível (à parte as correntes de
fugas, e para níveis de tensão abaixo
da tensão de breakdown).
(Nota: Há também
região de depleção em
n+, mas como ND>>
NA, em p- a sua
extensão é muito
menor)
Vs>0
IDS≅0
Região de depleção
(iões-, não disponíveis
para condução)
Vg<<0
VD>0
FEUP
VGT
3
MOSFET
EIII
MOSFET: Modos de operação básicos
Vg> 0
2. Região de Depleção/Inversão
- Um Vg positivo actua de uma forma
capacitiva para colocar uma igual
variação de carga, Q+ e Q-, na porta e à
superfície do substrato, respectivamente.
As lacunas serão repelidas, sendo
possível encontrar um Vg que induza uma
situação de depleção (ausência de cargas
móveis na região de substrato por baixo
da porta). Portanto, a corrente será nula
nesta circunstância.
- Com Vg a aumentar, o campo eléctrico
nas regiões de dreno e fonte faz deslocar
cargas destas regiões para o substrato,
fazendo inverter a polaridade do canal
tornando-se assim do tipo n.
FEUP
n+
-
-
-
-
n+
pCanal invertido
Região de depleção (iões-,
não
disponíveis
para
condução)
- Se Vg é tal que a concentração de electrões no
canal é inferior à de p-: transístor opera na região
de inversão fraca ou sublimiar. Se Vg é tal que a
concentração do canal (n) iguala ou se torna
superior a p-: transístor opera na inversão forte.
À tensão Vgs, para o qual se torna verdade a
inversão forte, chama-se tensão de limiar (Vt).
VGT
MOSFET
4
2
EIII
MOSFET: modelo eléctrico simples – Inversão forte
• As tensões no MOSFET são sempre referenciadas ao
substrato.
VS≡VSB
VD≡VDB
VG≡VGB
VGS≡VGB-VSB
VDS≡VDB-VSB
VGD≡VGB-VDB
D
VGD
IDS
G
B
VGS
VDS
S
• O modelo é representado por um conjunto de equações que relacionam IDS
com as restantes tensões no transístor. São portanto relações formais que
pretendem prever o comportamento físico do dispositivo.
FEUP
VGT
5
MOSFET
Modelo de carga laminar
EIII
• Este é o modelo mais simples e corresponde à assunção de que o canal de
inversão tem uma profundidade infinitesimal.
dR
L e W são o comprimento e largura do
canal, respectivamente
• A corrente é devida a duas
componentes: difusão e deriva. Embora
neste modelo se considerem campos
eléctricos fracos, na inversão forte são
suficientemente elevados para que só se
considere a componente de deriva.
• Condutividade do canal por quadrado:
1
σ s = µ nQn (x) =
ρs
Mobilidade dos electrões
(lacunas no canal de tipo p)
FEUP
IDS
D
S
w
dx
→0
L
• Notar que: R = ρ L
, então RL=W =ρ/h. Ou
W ⋅h
seja, a resistência de um quadrado é independente
do valor de L e W (h é constante para cada
material.
Isto é válido para o polisilício, regiões n+(p-)...
MOSFET
VGT
6
3
Modelo de carga laminar: Tríodo
EIII
VGS
• Considerando o canal uniforme entre
o dreno e a fonte, podemos definir
uma capacidade total Cgb, entre a
porta e o canal de inversão, como:
ε (L − LD )W
Cgb = ox
tox
• É mais comum designar-se esta
capacidade por Cox, e o seu valor por
unidade de àrea é:
ε ox
⇒ Cox = Cox' ⋅ W ⋅ L
tox
• Carga por unidade de área no canal:
Cox' =
Vch(x)
V(x) dx
x
L
x
VDS
• Resistência e tensão incrementais:
dR = ρ s
dx
I
⇔ dV (x ) = I DS ⋅ dR = DS dx
W
Wµ nQn
2
VDS
' W
I DS = µn Cox (VGS − VT )VDS −
L
2
• Manipulando e integrando: VGS ≥ VT
Região linear ou de tríodo (VGS − VT ) ≥ VDS
Qn (x ) = −C 'ox (VG − VCH ( x ) − VT ) = −C 'ox (VGS − V ( x) − VT )
FEUP
VGT
7
MOSFET
Modelo de carga laminar: Saturação
EIII
• Conforme VDS aumenta, a densidade de carga junto ao
dreno diminui, de facto:
Qn (L ) = Cox' (VG − VD − VT ) = Cox' (VGS − VDS − VT ) = Cox' ((VGS − VT ) − VDS )
Vch(L)
• Se VDS=VGS-VT então Qn(L)=0, ocorre o pinch-off. A partir daqui pode-se,
numa aproximação de primeiro grau, afirmar que a carga total no canal é
constante. Portanto basta substituir VDS=VGS-VT na equação de IDS em tríodo,
resultando na seguinte equação:
Região de saturação
FEUP
MOSFET
1
2
' W
I DS = 2 µ nCox L (VGS − VT )
VGS ≥ VT
(V − V ) ≤ V
T
DS
GS
VGT
8
4
EIII
I DS = µ nCox'
Modelo de carga laminar: Modulação de canal
VDS
W
(V − VT )2
Lelect GS
Lelect = L − ∆L
(VGS − VT )
∆L
(Largura da região de
depleção.)
• Variação de IDS com VDS?
∂I DS
1 ∂∆L
I DS
Lelect ∂VDS
∂VDS
∆L ≅
2ε si
2ε si
V
V − (VGS − VT ) + φ0
+φ =
qN A Dcanal 0
qN A DS
λ - Modulação de canal
I DS = µ nCox'
λ=
(
(
W
(V − VT )2 1 + λ VDS − VDSsat
L GS
2ε si
qN A
2 L VDS − (VGS − VT ) + φ 0
))
Implante
Substrato
N N
φ0 = Vt ln A 2 D
ni
Potencial de contacto da junção PN
Nota: Considera-se ∆L como sendo a extensão correspondente à
depleção na região p- pois ND>>N A
FEUP
VGT
9
MOSFET
EIII
Modelo de carga laminar: Efeito de corpo
• O aumento da tensão de fonte em
relação ao substrato faz alargar a
região de depleção, encurtando a
profundidade do canal, e portanto
menor será a carga total no canal.
Quer isto dizer que IDS diminui
com o aumento de VSB.
• A diminuição de corrente é
reflectida por uma alteração na
tensão de limiar.
VT = VTo + γ
γ =
( VSB + 2φ
F
− 2φ F
)
2qN Aε si
Cox'
φF – Potencial de Fermi: Definese como o potencial de contacto
entre o material extrínseco e o
intrínseco.
N
φ F = Vt ln
FEUP
MOSFET
A ou D
ni
VGT
10
5
MOSFET: Capacidades Parasitas
EIII
Óxido
fino
Óxido
Grosso (FOX)
até 40.tox
CGB/2
CGB|ov=2C’oxW dLef=CGBO.Lef
L
Lef
W S
Lef=L-2Ld
Ld
D
Channel
Stop – NA+
Wef
CSB|ov=Cbottom + Csw =
Cj LS.Wef +CJSW(2 LS+ Wef)
CGS|ov=C’oxWefLd=CGSO.Wef
CGD|ov=C’oxW efLd=CGDO.Wef
Em princípio CSB=CDB
FEUP
VGT
11
MOSFET
MOSFET: Capacidades
EIII
G
S
D
Cgd
Cgso
Cox
CBC
Cjsb
Cgdo
Cdb
Cgs
Csb
Cgb
Cjdb
Sobreposição nos extremos da porta
Capacidade
Corte
Cgd
CGDO.W
Cdb
Cjdep
Cgb
Linear / Tríodo
1
Saturação / Pêntodo
W.L.C’ox+CGDOW
CGDO.W
2
Cjdep
Cjdep
C’ox.W.Lef+CGBO.L CGBO.L
Cgs
CGSO.W
Csb
Cjdep
1
W.L.C’ox+CGSOW
2
Cjdep
FEUP
MOSFET
CGBO.L
2
W.L.C’ox+CGSOW
3
Cjdep
VGT
12
6
MOSFET: Capacidades
EIII
.MODEL CMOSN NMOS LEVEL=3 TOX=3.0500E-08 [m] LD=1.0000E-07 [m] UO=670.9 [cm2/V]
+ CGDO=1.6983E-10 [F/m] CGSO=1.6983E-10 [F/m] CGBO=2.0013E-10 [F/m]
+ CJ=2.9258E-04 [F/m2] MJ=5.2218E-01 CJSW=1.2774E-10 [F/m] MJSW=1.0000E-01
+ PB=9.7901E-01 [V]
C jdep =
cj. AD
V DB
1 +
PB
MJ
+
CJSW .PD
V
1 + DB
PBSW
'
C ox
=
MJSW
ε ox 3,97 × 8,85.aF / µm
=
TOX
TOX
FEUP
VGT
13
MOSFET
EIII
MOSFET: Capacidades
Acumulação
C
Depleção
Capacidade de
má qualidade
Inversão forte
Capacidade de
razoável qualidade
VT
VGS
C = Cox' ⋅ W ⋅ L
FEUP
MOSFET
VGT
14
7
Modelos: Sumário
EIII
O transístor MOS –
região linear
Vgs> Vt
Vds < Vgs - Vt
- +
Óxido da porta
L
Vd
porta
-
fonte
corrente
+
Lef
β – factor de ganho do transístor
+I
dreno
d
Substracto p
Em SPICE
KP
UO
VTO
TOX
Kn(p) – transcondutância intrínseca do processo
mn(p) – mobilidade superficial
VT – tensão de limiar de condução (VSB=0)
C’ ox – capacidade unitária do óxido ( = eox / tox)
eox = 3.97 x 8,85 aF/µm
FEUP
VGT
15
MOSFET
Modelos: Sumário
EIII
O transístor MOS – região de saturação
1
I D = β (VGS − VT )2 (1 + λVDS )
2
Vds = tensão de pintch-off
Vgs> Vt
Vds = Vgs - Vt
- +
Vd
porta
fonte
corrente
dreno
Id
fonte
dreno
Id
saturação
FEUP
Vds > Vgs - Vt
porta
Óhmica,
linear
λ – coeficiente de modulação do canal
MOSFET
Em SPICE
LAMBDA
VGT
16
8
SPICE – modelo nível 1
EIII
Na região linear:
I DS = KP.
Vgs > Vt e Vds < Vgs - Vt
W
Vds
. Vgs - Vt .Vds(1 + λ.Vds )
L ef
2
Na região de Saturação
IDS =
Vgs > Vt e Vds > Vgs - Vt
KP W
2
.
.(Vgs - Vt ) .(1 + λ .Vds )
2 Leff
KP = µ.C'ox
Vt = Vt 0 + γ ( (2φp - Vbs ) − 2φp )
Leff = L - 2Xjl
γ=
2ε s Na
C'ox
C'ox =
φp =
kT Na
ln
q ni
εox
tox
FEUP
VGT
17
MOSFET
SPICE – modelo nível 1
EIII
SíMBOLO
Vt
KP
γ
2φf
λ
tox
Nb
Xjl
µo
SPICE
VTO
KP
GAMMA
PHI
LAMBDA
TOX
NSUB
LD
UO
DESCRIÇÃO
UNIDADES
Vt para vbs=0
Transcondutância
Efeito de corpo
Potencial de superfície em inversão
Modulação de canal
Espessura de Óxido
Dopagem de Substrato
Difusão lateral
Mobilidade de superfície
V
A/V2
V1/2
V
V-1
m
cm-3
m
cm2/V.s
Parâmetros de efeitos parasitas
Is
Js
φJ
FEUP
Cj
Mj
Cjsw
Mjsw
FC
Ccbo
Cgdo
Cgso
Rd
Rs
Rsh
IS
JS
PB
CJ
MJ
CJSW
MJSW
FC
CGBO
CGDO
CGSO
RD
RS
RSH
Corrente de Saturação da Junção
Densidade de Corrente de Saturação da Junção
Potencial da junção
Capacidade por área para Vbs=0
Coeficiente de graduação da junção
Capacidade de perímetro por metro para Vbs=0
Coeficiente de graduação da junção no perímetro
Coeficiente de junção polarizada directamente
Capacidade entre Porta e corpo
Capacidade entre Porta e Dreno
Capacidade entre Porta e Fonte
Resistência do Dreno
Resistência da Fonte
Resistência superficial entre fonte e dreno
MOSFET
A
A/m2
V
F/m2
-F/m
--F/m
F/m
F/m
Ω
Ω
Ω
VGT
18
9
SPICE – modelo nível 2
EIII
Na região linear:
IDS =
3
3
KP
W
Vds
2
.
. Vgs - Vfb - 2φf .Vds − γ (Vds - Vbs + 2φf )2 − (− Vbs + 2φf )2
1 − λ.Vds Leff
2
3
A tensão de limiar pode ser calculada a partir dos parâmetros físicos através da equação:
Vt0 = φ ms -
q.Nss
+ 2φf + γ
C'ox
2φ f
onde: φms = −
N D, poly Potencial de contacto
kT Na
entre porta e substrato
+ ln
ln
q ni
ni
Na região de Saturação:
1
1 − λ Vds
IDS = I D,sat
ID,sat é calculado pela expressão de IDS na região linear fazendo Vds=Vd,sat
2
VD, sat = Vgs - Vfb - 2φp + γ 2 1 - 1 + 2 ( Vgs - Vfb)
γ
Na região de Inversão fraca:
VON = V t +
Ids = Ion.e
nkT
q
n =1+
q
nkT
(Vgs - Von ).
qNfs
Cd
+
C'ox C'ox
φp=φf
Cd = Capacidade de depleção
Efeito da redução da mobilidade com o aumento de Vg
εs
Uc .tox
KP'= KP
ox
.
Vgs
Vt
Ut
Vds
ε
−
−
Ion=Ids em inversão forte, para Vgs=Von
Ue
O termo em parêntesis é limitado a 1
FEUP
VGT
19
MOSFET
SPICE – modelo nível 2
EIII
SÍMBOLO
Vt
KP
γ
2 φf
λ
tox
Nb
Nss
Nfs
Neff
Xj
Xjl
Tpg
µo
Uc
Ue
Ut
vmax
Xqc
δ
SPICE
VTO
KP
GAMMA
PHI
LAMBDA
TOX
NSUB
NSS
NFS
NEFF
XJ
LD
TPG
UO
UCRIT
UEXP
UTRA
VMAX
XQC
DELTA
DESCRIÇÃO
UNIDADES
Vt para vbs=0
Transcondutância
Efeito de corpo
Potencial de superfície em inversão
Modulação de canal
Espessura de Óxido
Dopagem de Substrato
Densidade de estados de superfície
Densidade de estados rápidos de superfície
Coeficiente de carga total de depleção
Profundidade da junção metalúrgica
Difusão lateral
Tipo do material do gate*
Mobilidade
Campo eléctrico crítico para mobilidade
Coeficiente exponencial para mobilidade
Coeficiente do campo transversal
Máxima velocidade de deriva de portadores
Fração de carga no canal atribuída ao dreno
Efeito da largura na tensão de limiar
FEUP
MOSFET
V
A/V2
V1/2
V
V-1
m
cm-3
cm-2
cm-2
--
m
m
-cm2/V.s
V/cm
--m/s
---
VGT
20
10
SPICE – modelo nível 3
EIII
Na região linear:
IDS = KP.
Fb =
W
1 + Fb
. Vgs - Vt -
.Vds .Vds
Leff
2
γ .Fs
+ Fn
2 2φp - Vbs
Fn =
εs.δ .π
4.C'ox.W
Efeito de canal curto (W)
σ representa empiricamente a dependência
de Vt com Vds
Vt = Vfb + 2φp - σ .Vds + γ .Fs 2φp - Vbs + Fn(2φp - Vbs)
σ =η
8.15x1021
C'ox.L3eff
Fs = 1 -
η - parâmetro ETA
Xj
Leff
Xjl + Wc
Wp
Xjl
. 1 −
Xj
Xj
Wp
Xj
+
No caso de não ser dado o valor de Kp
µeff =
µs
µs.Vds
1+
vmax.Leff
µs =
µ
1 + θ (Vgs - Vt) + θVbs
É usado o mesmo modelo do nível 2 para inversão fraca
FEUP
MOSFET
VGT
21
11