GEOMETRIA BÁSICA 2010-1
GGM00161-TURMA M1
Dirce Uesu Pesco
Geometria Espacial
15/06/2010
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução:
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
8 (V 2)
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
8 (V 2) V 10
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
2880o (V 2)360o
8 (V 2) V 10
Logo o prisma é pentagonal.
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
Lembre que:
2880 (V 2)360
8 (V 2) V 10
o
o
Logo o prisma é pentagonal.
Si (n 2).180o
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
Lembre que:
2880 (V 2)360
8 (V 2) V 10
o
o
Logo o prisma é pentagonal.
Si (n 2).180o
Si (5 2).180o 540o
Base pentagonal
PROPRIEDADE DE POLIEDROS CONVEXOS
A soma dos ângulos de todas as faces de um poliedro convexo
é:
S (V 2) 4r
onde V é o número de vértices e r é o ângulo reto.
Exercício: Determine a natureza de um prisma sabendo que a
o
soma dos ângulos internos de todas as suas faces vale 2880 .
Solução: 2880o (V 2)4.90o
Lembre que:
2880 (V 2)360
8 (V 2) V 10
o
o
Logo o prisma é pentagonal.
Si (n 2).180o
Si (5 2).180o 540o
Base pentagonal
S 2 540o 5 360o 2880o
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução:
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais,
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60o
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
5 3
2
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
Al 4 Aparalelogramo
5 3
2
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
5 3
2
Al 4 Aparalelogramo Al 4 3. 5 3 30 3 cm 2
2
PROPRIEDADE DE POLIEDROS CONVEXOS
Exercício2 : Calcule a área lateral do prisma obliquo de base
quadrada, cujas medidas estão indicadas na figura.
Unidade : centímetros.
Solução: São quatro paralelogramos que
compõem as arestas laterais, cuja base é:
3 cm, a altura corresponde a
h 5 sen 60
o
h
5 3
2
Al 4 Aparalelogramo Al 4 3. 5 3 30 3 cm 2
2
Exercício: encontre a área total e o volume do prisma
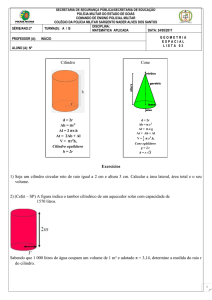
CILINDRO
Definição:
Considere α e β dois planos paralelos,
um círculo Г contido em α e uma
reta s que corta α e β.
CILINDRO
Definição:
Considere α e β dois planos paralelos,
um círculo Г contido em α e uma
reta s que corta α e β.
Para cada ponto X de Г, trace uma
reta paralela a s e seja X’ tal ponto
de interseção com β.
CILINDRO
Definição:
Considere α e β dois planos paralelos,
um círculo Г contido em α e uma
reta s que corta α e β.
Para cada ponto X de Г, trace uma
reta paralela a s e seja X’ tal ponto
de interseção com β.
Chama-se cilindro circular ou cilindro
a reunião de todos os segmentos XX’,
onde X pertence a Г(região circular).
CILINDRO
Elementos:
i) 2 bases: círculos congruentes situados em planos paralelos.
CILINDRO
Elementos:
i) 2 bases: círculos congruentes situados em planos paralelos.
ii) geratrizes:
segmentos com uma das extremidades
em um ponto da circunferência de centro O e raio r e outra no ponto correspondente da circunferência de centro
O’ e raio r.
CILINDRO
Elementos:
i) 2 bases: círculos congruentes situados em planos paralelos.
ii) geratrizes:
segmentos com uma das extremidades
em um ponto da circunferência de centro O e raio r e outra no ponto correspondente da circunferência de centro
O’ e raio r.
iii) O eixo do cilindro é a reta determinada pelos centros das
bases.
CILINDRO
Elementos:
i) 2 bases: círculos congruentes situados em planos paralelos.
ii) geratrizes:
segmentos com uma das extremidades
em um ponto da circunferência de centro O e raio r e outra no ponto correspondente da circunferência de centro
O’ e raio r.
iii) O eixo do cilindro é a reta determinada pelos centros das
bases.
- r é o raio da base.
CILINDRO
Elementos:
i) 2 bases: círculos congruentes situados em planos paralelos.
ii) geratrizes:
segmentos com uma das extremidades
em um ponto da circunferência de centro O e raio r e outra no ponto correspondente da circunferência de centro
O’ e raio r.
iii) O eixo do cilindro é a reta determinada pelos centros das
bases.
- r é o raio da base.
- a altura de um cilindro é a distância h entre os planos das bases.
CILINDRO
Superfícies:
CILINDRO
Superfícies:
Superfície lateral:
Superfície total:
CILINDRO
Superfícies:
Superfície lateral:
é a reunião das geratrizes.
Superfície total:
CILINDRO
Superfícies:
Superfície lateral:
é a reunião das geratrizes.
Superfície total:
é a reunião da superfície lateral com os círculos das bases.
CILINDRO
Classificação:
CILINDRO
Classificação:
Cilindro circular obliquo:
CILINDRO
Classificação:
Cilindro circular obliquo: se as geratrizes são obliquas aos planos
das bases.
CILINDRO
Classificação:
Cilindro circular obliquo: se as geratrizes são obliquas aos planos
das bases.
Cilindro circular reto:
CILINDRO
Classificação:
Cilindro circular obliquo: se as geratrizes são obliquas aos planos
das bases.
Cilindro circular reto: se as geratrizes são perpendiculares aos
planos das bases.
CILINDRO
Classificação:
Cilindro circular obliquo: se as geratrizes são obliquas aos planos
das bases.
Cilindro circular reto: se as geratrizes são perpendiculares aos
planos das bases.
Cilindro de revolução :
CILINDRO
Classificação:
Cilindro circular obliquo: se as geratrizes são obliquas aos planos
das bases.
Cilindro circular reto: se as geratrizes são perpendiculares aos
planos das bases.
Cilindro de revolução : é o cilindro circular reto e é gerado pela rotação de um retângulo em torno de um eixo, que contém um dos seus
lados.
CILINDRO
Seção Meridiana :
CILINDRO
Seção Meridiana :
É a interseção do cilindro com um plano que contém a reta OO’,
denominada pelos centros das bases.
CILINDRO
Seção Meridiana :
É a interseção do cilindro com um plano que contém a reta OO’,
denominada pelos centros das bases.
A seção meridiana de um cilindro obliquo é um paralelogramo.
(Faça um desenho que represente esta seção).
CILINDRO
Seção Meridiana :
É a interseção do cilindro com um plano que contém a reta OO’,
denominada pelos centros das bases.
A seção meridiana de um cilindro obliquo é um paralelogramo.
(Faça um desenho que represente esta seção).
CILINDRO
Seção Meridiana :
É a interseção do cilindro com um plano que contém a reta OO’,
denominada pelos centros das bases.
A seção meridiana de um cilindro obliquo é um paralelogramo.
(Faça um desenho que represente esta seção).
A seção meridiana de um cilindro
reto é um retângulo. Veja figura
ao lado .
CILINDRO
Cilindro equilátero:
CILINDRO
Cilindro equilátero:
É um cilindro cuja seção meridiana é um quadrado.
CILINDRO
Cilindro equilátero:
É um cilindro cuja seção meridiana é um quadrado.
Portanto
CILINDRO
Cilindro equilátero:
É um cilindro cuja seção meridiana é um quadrado.
Portanto
g = h =2r
CILINDRO
Área Lateral de um Cilindro circular reto
CILINDRO
Área Lateral de um Cilindro circular reto
A área lateral de um cilindro circular reto ou cilindro de revolução
é equivalente a um retângulo de dimensões 2 r (comprimento
da circunferência da base) e h (altura do cilindro)
CILINDRO
Área Lateral de um Cilindro circular reto
A área lateral de um cilindro circular reto ou cilindro de revolução
é equivalente a um retângulo de dimensões 2 r (comprimento
da circunferência da base) e h (altura do cilindro)
CILINDRO
Área Lateral de um Cilindro circular reto
A área lateral de um cilindro circular reto ou cilindro de revolução
é equivalente a um retângulo de dimensões 2 r (comprimento
da circunferência da base) e h (altura do cilindro)
Ou seja, a área lateral do cilindro circular reto é:
2 r h
CILINDRO
Área Total de um Cilindro circular reto
CILINDRO
Área Total de um Cilindro circular reto
É a soma da área lateral Al com as áreas das duas bases
B r2
CILINDRO
Área Total de um Cilindro circular reto
É a soma da área lateral Al com as áreas das duas bases
B r2
CILINDRO
Área Total de um Cilindro circular reto
É a soma da área lateral Al com as áreas das duas bases
B r2
A área total do cilindro circular reto é:
CILINDRO
Área Total de um Cilindro circular reto
É a soma da área lateral Al com as áreas das duas bases
B r2
A área total do cilindro circular reto é:
At 2 r (h r )
CILINDRO
Volume do Cilindro
CILINDRO
Volume do Cilindro
O volume de um Cilindro é o produto da área da base pela medida da
altura.
CILINDRO
Volume do Cilindro
O volume de um Cilindro é o produto da área da base pela medida da
altura.
Prova: Considere
- um cilindro S1 de altura h e área da base B1 B e um prisma S 2
de altura h e área da base B2 B .
CILINDRO
Volume do Cilindro
O volume de um Cilindro é o produto da área da base pela medida da
altura.
Prova: Considere
- um cilindro S1 de altura h e área da base B1 B e um prisma S 2
de altura h e área da base B2 B .
CILINDRO
Volume do Cilindro
-
Suponha que os dois sólidos têm as bases num mesmo plano, α e
estão num dos semi-espaços determinados por α.
CILINDRO
Volume do Cilindro
-
-
Suponha que os dois sólidos têm as bases num mesmo plano, α e
estão num dos semi-espaços determinados por α.
Qualquer plano β paralelo a α, que secciona o cilindro também
secciona o prisma e as seções têm áreas iguais.
CILINDRO
Volume do Cilindro
-
-
Suponha que os dois sólidos têm as bases num mesmo plano, α e
estão num dos semi-espaços determinados por α.
Qualquer plano β paralelo a α, que secciona o cilindro também
secciona o prisma e as seções têm áreas iguais.
B1' B1 , B2' B2 , B1 B2 B B1' B2'
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri,
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro VPrisma
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro VPrisma
Como VPrisma B2 h B h
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro VPrisma
Como VPrisma B2 h B h VCilindro B h
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro VPrisma
Como VPrisma B2 h B h VCilindro B h
V B h
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro VPrisma
Como VPrisma B2 h B h VCilindro B h
Se B r 2
V B h
CILINDRO
Volume do Cilindro
Então, pelo Princípio de Cavalieri, o cilindro e o prisma têm volumes
iguais.
VCilindro VPrisma
Como VPrisma B2 h B h VCilindro B h
Se B r 2
VCilindro r 2 h
V B h
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
Solução: Tudo de tinta é um cilindro cujo diâmetro da base é 2 mm e
altura 10 cm = 100 mm.
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
Solução: Tudo de tinta é um cilindro cujo diâmetro da base é 2 mm e
altura 10 cm = 100 mm.
V .12.100 100 mm3
O volume de tinta é:
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
Solução: Tudo de tinta é um cilindro cujo diâmetro da base é 2 mm e
altura 10 cm = 100 mm.
V .12.100 100 mm3
O volume de tinta é:
3
Em um dia gasto 2 mm de tinta, então:
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
Solução: Tudo de tinta é um cilindro cujo diâmetro da base é 2 mm e
altura 10 cm = 100 mm.
V .12.100 100 mm3
O volume de tinta é:
3
Em um dia gasto 2 mm de tinta, então:
1 dia x
2 mm 3
- 100 mm 3
CILINDRO
Volume do Cilindro
Exercício:
Um tubo de tinta de uma caneta esferográfica tem 2 mm de diâmetro
e 10 cm de comprimento. Vamos supor que você gasta 2 mm3 de tinta
por dia. Nessas condições a tinta de sua caneta esferográfica durará
quantos dias?
Solução: Tudo de tinta é um cilindro cujo diâmetro da base é 2 mm e
altura 10 cm = 100 mm.
V .12.100 100 mm3
O volume de tinta é:
3
Em um dia gasto 2 mm de tinta, então:
1 dia x
2 mm 3
- 100 mm 3
x
1.100
50 dias
2
CONE
Definição:
CONE
Definição:
CONE
Definição:
Considere um círculo Г contido no plano α e seja V um ponto fora do
plano α. Para cada ponto X pertencente a α, trace o segmento VX.
CONE
Definição:
Considere um círculo Г contido no plano α e seja V um ponto fora do
plano α. Para cada ponto X pertencente a α, trace o segmento VX.
Chama-se cone circular ou cone à reunião dos segmentos VX.
CONE
Elementos
CONE
Elementos
uma base : círculo de centro O e raio r,
CONE
Elementos
uma base : círculo de centro O e raio r,
vértice: o ponto V.
CONE
Elementos
uma base : círculo de centro O e raio r,
vértice: o ponto V.
geratrizes : segmentos ligando o vértice V a um ponto da circunferência da base.
CONE
Elementos
uma base : círculo de centro O e raio r,
vértice: o ponto V.
geratrizes : segmentos ligando o vértice V a um ponto da circunferência da base.
A altura de um cone é a distância entre o
Vértice e o plano da base.
CONE
Elementos
uma base : círculo de centro O e raio r,
vértice: o ponto V.
geratrizes : segmentos ligando o vértice V a um ponto da circunferência da base.
A altura de um cone é a distância entre o
Vértice e o plano da base.
Superfície lateral: reunião das geratrizes.
CONE
Elementos
uma base : círculo de centro O e raio r,
vértice: o ponto V.
geratrizes : segmentos ligando o vértice V a um ponto da circunferência da base.
A altura de um cone é a distância entre o
Vértice e o plano da base.
Superfície lateral: reunião das geratrizes.
Superfície total : reunião da superfície
lateral com o círculo da base.
CONE
Classificação
CONE
Classificação
Pela posição de VO em relação ao plano da base.
CONE
Classificação
Pela posição de VO em relação ao plano da base.
CONE
Classificação
Pela posição de VO em relação ao plano da base.
Cone circular obliquo – Se VO é obliqua ao plano da base.
CONE
Classificação
Pela posição de VO em relação ao plano da base.
Cone circular obliquo – Se VO é obliqua ao plano da base.
Cone circular reto ou cone de revolução - se VO é perpendicular ao
plano da base.
CONE
Seção meridiana
CONE
Seção meridiana
Interseção do cone com um plano que contém VO.
CONE
Seção meridiana
Interseção do cone com um plano que contém VO.
CONE
Seção meridiana
Interseção do cone com um plano que contém VO.
A seção meridiana de um cone circular reto ou cone de revolução é um
Triângulo isósceles.
CONE
Cone equilátero
CONE
Cone equilátero
CONE
Cone equilátero
Cone cuja seção meridiana é um triângulo equilátero.
CONE
Áreas Lateral e Total de um cone circular reto
CONE
Áreas Lateral e Total de um cone circular reto
A superfície lateral de um cone circular reto (cone de revolução) de raio
da base r e geratriz g é equivalente a um setor circular de raio g e
comprimento do arco 2 r.
CONE
Áreas Lateral e Total de um cone circular reto
A superfície lateral de um cone circular reto (cone de revolução) de raio
da base r e geratriz g é equivalente a um setor circular de raio g e
comprimento do arco 2 r.
CONE
Áreas Lateral e Total de um cone circular reto
A superfície lateral de um cone circular reto (cone de revolução) de raio
da base r e geratriz g é equivalente a um setor circular de raio g e
comprimento do arco 2 r.
Sendo θ o ângulo do setor, temos que :
2 r
360 r
rad ou
graus
g
g
CONE
Áreas Lateral e Total de um cone circular reto
A superfície lateral de um cone circular reto (cone de revolução) de raio
da base r e geratriz g é equivalente a um setor circular de raio g e
comprimento do arco 2 r.
Sendo θ o ângulo do setor, temos que :
2 r
360 r
rad ou
graus
g
g
CONE
Áreas Lateral e Total de um cone circular reto
A superfície lateral de um cone circular reto (cone de revolução) de raio
da base r e geratriz g é equivalente a um setor circular de raio g e
comprimento do arco 2 r.
Asetor
Sendo θ o ângulo do setor, temos que :
2 r
360 r
rad ou
graus
g
g
2 r.g g 2
2
2
CONE
Áreas Lateral e Total de um cone circular reto
Área lateral do cone:
Comprimento do arco
2 g
2 r
área do setor
________
________
g2
Al
Al r g
2 r g 2
Al
2 g
CONE
Áreas Lateral e Total de um cone circular reto
Área lateral do cone:
Comprimento do arco
2 g
2 r
área do setor
________
________
g2
Al
Al r g
2 r g 2
Al
2 g
CONE
Áreas Lateral e Total de um cone circular reto
Área lateral do cone:
Comprimento do arco
2 g
2 r
área do setor
________
________
g2
Al
Al r g
Ou ainda, a área do setor circular é
Asetor
2 r.g
r g Al
2
2 r g 2
Al
2 g
CONE
Áreas Lateral e Total de um cone circular reto
Área total :
At Al B
CONE
Áreas Lateral e Total de um cone circular reto
Área total :
At Al B
onde a área da base é
B r2
CONE
Áreas Lateral e Total de um cone circular reto
Área total :
At Al B
onde a área da base é
B r2
Logo
At r g r 2
CONE
Áreas Lateral e Total de um cone circular reto
Área total :
At Al B
onde a área da base é
B r2
Logo
At r g r 2 At r ( g r )
CONE
O volume do Cone
CONE
O volume do Cone
O volume do cone é um terço do produto da área da base pela medida
da altura.
CONE
O volume do Cone
O volume do cone é um terço do produto da área da base pela medida
da altura.
2
B
r
, temos que V 1 r 2 h,
Se
3
CONE
O volume do Cone
O volume do cone é um terço do produto da área da base pela medida
da altura.
2
B
r
, temos que V 1 r 2 h,
Se
3
Exercício:
Use o Princípio de Cavalieri para demonstrar o resultado acima.
ESFERA
Definição
ESFERA
Definição
Considere um ponto O e r um número real positivo. Denominamos
esfera de centro O e raio r o conjunto dos pontos P do espaço cuja
distância OP é menor ou igual a r.
ESFERA
Definição
Considere um ponto O e r um número real positivo. Denominamos
esfera de centro O e raio r o conjunto dos pontos P do espaço cuja
distância OP é menor ou igual a r.
ESFERA
Definição
Considere um ponto O e r um número real positivo. Denominamos
esfera de centro O e raio r o conjunto dos pontos P do espaço cuja
distância OP é menor ou igual a r.
Superfície da esfera de raio r e centro O:
ESFERA
Definição
Considere um ponto O e r um número real positivo. Denominamos
esfera de centro O e raio r o conjunto dos pontos P do espaço cuja
distância OP é menor ou igual a r.
Superfície da esfera de raio r e centro O:
ao conjunto dos pontos do espaço cuja distância
OP seja igual a r.
ESFERA
Definição
Considere um ponto O e r um número real positivo. Denominamos
esfera de centro O e raio r o conjunto dos pontos P do espaço cuja
distância OP é menor ou igual a r.
Superfície da esfera de raio r e centro O:
ao conjunto dos pontos do espaço cuja distância
OP seja igual a r.
OBS:
A superfície da esfera é também superfície de revolução gerada pela
rotação de uma semicircunferência com extremidades no eixo.
ESFERA
Seção plana de uma esfera:
ESFERA
Seção plana de uma esfera:
ESFERA
Seção plana de uma esfera: é um círculo.
ESFERA
Seção plana de uma esfera: é um círculo.
Se o plano secante passa pelo centro da esfera,
ESFERA
Seção plana de uma esfera: é um círculo.
Se o plano secante passa pelo centro da esfera, temos como
seção um círculo máximo da esfera.
ESFERA
Seção plana de uma esfera: é um círculo.
Se o plano secante passa pelo centro da esfera, temos como
seção um círculo máximo da esfera.
Se r é o raio da esfera,d a distância do
plano secante ao centro e s=O’A é o
raio da seção, vale :
ESFERA
Seção plana de uma esfera: é um círculo.
Se o plano secante passa pelo centro da esfera, temos como
seção um círculo máximo da esfera.
Se r é o raio da esfera,d a distância do
plano secante ao centro e s=O’A é o
raio da seção, vale :
s2 r 2 d 2
ESFERA
Área e Volume
A área da superfície de uma esfera de raio r é
A 4 r 2
Exercício: Deduza a fórmula acima. (pagina 231)
O volume da esfera de raio r é:
4
V r3
3
´