ficha áreas e volumes de sólidos de revolução

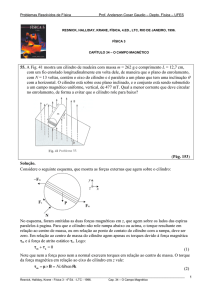
Sólidos de revolução
Cilindro de revolução é o
sólido gerado pela rotação
de um retângulo [ABCD]
numa volta completa em
torno de um dos seus lados.
Vcilindro = área da base * altura
Vcilindro = p * r * h
2
1.
GEOMETRIA DO CÍRCULO
Cone de revolução é o
sólido gerado pela rotação
de um triângulo retângulo
[ABC] numa volta completa
em torno de um dos catetos.
Esfera é o sólido gerado pela
rotação de um semicírculo
numa volta completa em
torno do diâmetro.
t
11
ÁREAS E VOLUMES DE SÓLIDOS DE REVOLUÇÃO
2.
Que quantidade de ouro (em mililitros) é necessária para o fabrico de 1000 bolinhas esféricas e maciças com 1 cm de diâmetro? (Considera p = 3,14.)
3.
Uma lata com a forma cilíndrica tem diâmetro interno igual a 8,4 cm. Sabendo que 1 ’ = 1 dm3,
qual deve ser a altura para que possa conter 1 ’ de água? Apresenta o resultado aproximado
às unidades.
4.
Para construir a cafeteira da figura ao lado efetuou-se um corte num
cone oco (de espessura desprezável), de 60 cm de altura, por um plano
paralelo ao plano da base e que interseta a altura no seu ponto médio.
Sabendo que d = 10 cm e que 1 ’ = 1000 cm3, determina quantos litros
de água são necessários para encher a cafeteira. (Considera p = 3,14.)
©
FICHA
4
1
Vcone = * área da base *altura Vesfera = * p * r3
3
3
1
Vcone = p * r2 * h
3
A figura representa dois cones de revolução, iguais, inscritos num cilindro oco, de espessura desprezável, de bases
coincidentes com as bases dos cones.
MÓDULO 14
AD = 2 * AB = 4 cm
A reta r, eixo do cilindro, contém a sua altura [AD].
1.1. Qual é a posição relativa das retas r e DC? Justifica.
Exames oficiais (adaptado)
5.
1.2. Determina o comprimento da geratriz de cada um dos cones.
Para construir a caixa de madeira representada na figura, fez-se num cilindro maciço uma
cavidade semiesférica cujo raio é igual à altura do cilindro. Considerando p = 3,14 e sabendo
que a altura do cilindro é 10 cm, determina:
5.1. a capacidade da caixa, em cm3.
1.3. Determina o volume do espaço não preenchido pelos cones de revolução dentro do cilindro.
(Considera p = 3,14.) Sempre que, nos cálculos intermédios, procederes a arredondamentos, conserva duas casas decimais. Indica o resultado arredondado às unidades.
26
t
©
Exames oficiais (adaptado)
5.2. o volume da madeira da caixa, em dm3.
Exames oficiais (adaptado)
27