Correção atividade Trigonometria Básica – 2os. anos

Correção atividade Trigonometria Básica – 2os. anos
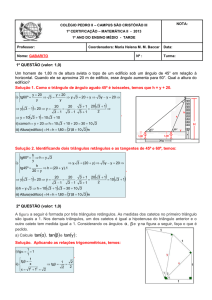
1) No triângulo da figura o lado AB mede 3 unidades, o
lado AC mede 4 unidades. Mategildo concluiu que o
seno do ângulo β é igual a:
O seno de um ângulo, no
triângulo retângulo, é igual a razão :
. Na figura a hipotenusa (lado
BC) não foi dada a sua dimensão. É
necessário calcular com o teorema de
Pitágoras:
logo:
Resposta correta: alternativa que continha 4/5.
2) Em um triângulo retângulo qualquer, podemos calcular o cosseno
de um ângulo usando a razão:
R:
cos(ângulo) = lado adjacente / hipotenusa
Correção atividade Trigonometria Básica – 2os. anos
3) A soma dos três ângulos internos de um triângulo
qualquer é sempre igual a:
R: A soma Si dos ângulos internos de um polígono convexo de n lados
é
o
dada por: Si = (n – 2) . 180 . Como o triângulo possui 3 lados, isto é, n= 3, temos:
Si = (3-2).180o
Si = 180o
4) A soma dos ângulos internos de um hexágono, polígono de seis
lados (vide imagem), é sempre igual a:
R: Caso semelhante ao exercício anterior.
Si = (6-2).180o
Si = 720o
Correção atividade Trigonometria Básica – 2os. anos
5) Uma torre vertical de altura 12 metros é vista sob
um ângulo de 30° por uma pessoa que se encontra a
uma distância X da sua base e cujos olhos estão no mesmo plano
horizontal dessa base
(passe o mouse na figura
para vê-la ampliada), Ao
calcular a distância X
encontramos um valor
entre:
R:
Logo a distância X está entre 20 m e 21 m.
Correção atividade Trigonometria Básica – 2os. anos
6) A dona Matematilda precisa calcular o
perímetro do triângulo retângulo ABC da
figura. Ela sabe que a medida do lado BC = 10
m e o cosseno do ângulo alfa = 0,6. Com esses
dados dona Matematilda calculou o perímetro do triângulo
ABC como
sendo igual a:
R: O lado BC = 10m é a hipotenusa do triângulo retângulo ABC. Podemos
calcular o lado AB usando a relação:
=6
O lado AC pode ser calculado com o teorema de Pitágoras, pois o triângulo
é retângulo e conhecemos a medida dos outros dois lados:
O perímetro é igual a soma da medida de todos os lados:
10 m + 6 m + 8 m = 24
m
Correção atividade Trigonometria Básica – 2os. anos
7) Uma empresa de fornecimento de energia, ao
instalar a rede elétrica numa fazenda, precisou
colocar dois postes em lados opostos de um lago
para permitir a passagem da fiação. Com isso surgiu um pequeno
problema: para fazer o projeto da rede, seria necessário saber a
distância entre os postes A e C, e a presença do lago impedia a
medição direta desta distância. Um dos engenheiros posicionou-se
em um local B onde era possível visualizar os dois postes e medir a
distância entre eles. Com um aparelho apropriado ele mediu o
ângulo entre a linha de visão dele e os postes, obtendo 120° . Um
auxiliar mediu a distância do poste mais afastado do engenheiro o
obteve 100 m; um outro auxiliar mediu o ângulo entre a linha do
poste mais próximo do engenheiro e a linha entre os postes,
obtendo 45° . Com estas informações, o engenheiro sorriu. Ele já
consegueria calcular a distÂncia entre os postes.A distância,
aproximada,
encontrada pelo
engenheiro entre
os postes foi de:
R: O triângulo não
é retângulo.
Conhecemos o
lado BC e seu
ângulo oposto.
Queremos calcular a medida do lado AC que, também, conhecemos o
ângulo oposto. Vamos utilizar a lei dos senos para descobrir a medida d.
Obs.: sen 45o =
Correção atividade Trigonometria Básica – 2os. anos
Substituindo os valores dos senos nas razões, temos:
Logo a distância, aproximada, encontrada pelo engenheiro foi 122
m.
8) O ângulo agudo de um losango mede 20° e seus lados medem 5 cm. As
medidas das diagonais maior e menor do losango serão,
respectivamente:
(considere cos 20° = 0,94)
R: Vamos calcular a medida da diagonal menor
recorrendo à lei dos cossenos:
A diagonal menor divide o losango em dois triângulos
semelhantes e isósceles. A diagonal maior intercepta
a diagonal menor no centro.
A medida h é metade da diagonal maior.
Recorrendo ao teorema de Pitágoras, temos:
D = 2.h
D = 2. 4,9
D = 9,8 cm
retorna página principal