Lista de Questões para a RECUPERAÇÃO FINAL

3ª série EM - Lista de Questões para a RECUPERAÇÃO FINAL - FÍSICA
01. Um edifício projeta no solo uma sombra de 40 m. No mesmo instante, um observador toma uma haste vertical de
20 cm e nota que sua sombra mede 80 cm.
a) Qual a altura do edifício?
b) Por que a sombra do prédio pode ser formada? Explique o princípio Físico que permite a formação de sombras e
penumbras.
02. Mediu-se o módulo da velocidade da luz amarela de sódio propagando-se num sólido e obteve-se o valor
8
2,00. 10 m/s. Qual o índice de refração absoluto desse sólido, para a luz de sódio?
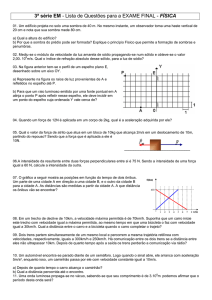
03. Na figura anterior tem-se o perfil de um espelho plano E,
desenhado sobre um eixo OY.
a) Represente na figura os raios de luz provenientes de A e
refletidos no espelho até P.
b) Para que um raio luminoso emitido por uma fonte pontual em A
atinja o ponto P após refletir nesse espelho, ele deve incidir em
um ponto do espelho cuja ordenada Y vale cerca de?
04. Quando um força de 12N é aplicada em um corpo de 2kg, qual é a aceleração adquirida por ele?
05. Qual o valor da força de atrito que atua em um bloco de 10kg que alcança 2m/s em um deslocamento de 10m,
partindo do repouso? Sendo que a força que é aplicada a ele é
10N.
06.A intensidade da resultante entre duas forças perpendiculares entre si é 75 N. Sendo a intensidade de uma força
igual a 60 N, calcule a intensidade da outra.
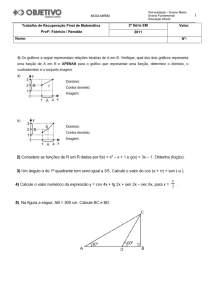
07. O gráfico a seguir mostra as posições em função do tempo de dois ônibus.
Um parte de uma cidade A em direção a uma cidade B, e o outro da cidade B
para a cidade A. As distâncias são medidas a partir da cidade A. A que distância
os ônibus vão se encontrar?
08. Em um trecho de declive de 10km, a velocidade máxima permitida é de 70km/h. Suponha que um carro inicie
este trecho com velocidade igual a máxima permitida, ao mesmo tempo em que uma bicicleta o faz com velocidade
igual a 30km/h. Qual a distância entre o carro e a bicicleta quando o carro completar o trajeto?
09. Dois trens partem simultaneamente de um mesmo local e percorrem a mesma trajetória retilínea com
velocidades, respectivamente, iguais a 300km/h e 250km/h. Há comunicação entre os dois trens se a distância entre
eles não ultrapassar 10km. Depois de quanto tempo após a saída os trens perderão a comunicação via rádio?
10. Um automóvel encontra-se parado diante de um semáforo. Logo quando o sinal abre, ele arranca com aceleração
5m/s², enquanto isso, um caminhão passa por ele com velocidade constante igual a 10m/s.
a) Depois de quanto tempo o carro alcança o caminhão?
b) Qual a distância percorrida até o encontro.
8
11. Uma onda luminosa propaga-se no vácuo, sabendo-se que seu comprimento é de 3.10 m podemos afirmar que o
período desta onda será?
12. Em filmes de ficção científica é muito comum observarmos naves espaciais que, durante combates em pleno
cosmo (onde reina o vácuo), disparam umas contra as outras, produzindo estrondos emocionantes. Esse fato é uma
realidade? Explique?
13. A propagação da luz envolve, necessariamente:
a) movimento de matéria.
b) Produção de energia.
c) Transporte de matéria.
d) Transporte de energia.
e) Transformação de energia.
14. Qual a potência média que um corpo desenvolve quando aplicada a ele uma força horizontal com intensidade
igual a 12N, por um percurso de 30m, sendo que o tempo gasto para percorrê-lo foi 10s?
15. Qual o trabalho realizado por um corpo de massa 10kg que inicia um percurso com velocidade 10m/s² até parar?
16. Uma bola de pingue-pongue rola sobre uma mesa com velocidade constante de 2m/s. Após sair da mesa, cai,
atingindo o chão a uma distância de 0,80m dos pés da mesa. Adote g= 10 m/s², despreze a resistência do ar e
determine:
a) a altura da mesa.
b) o tempo gasto para atingir o solo.
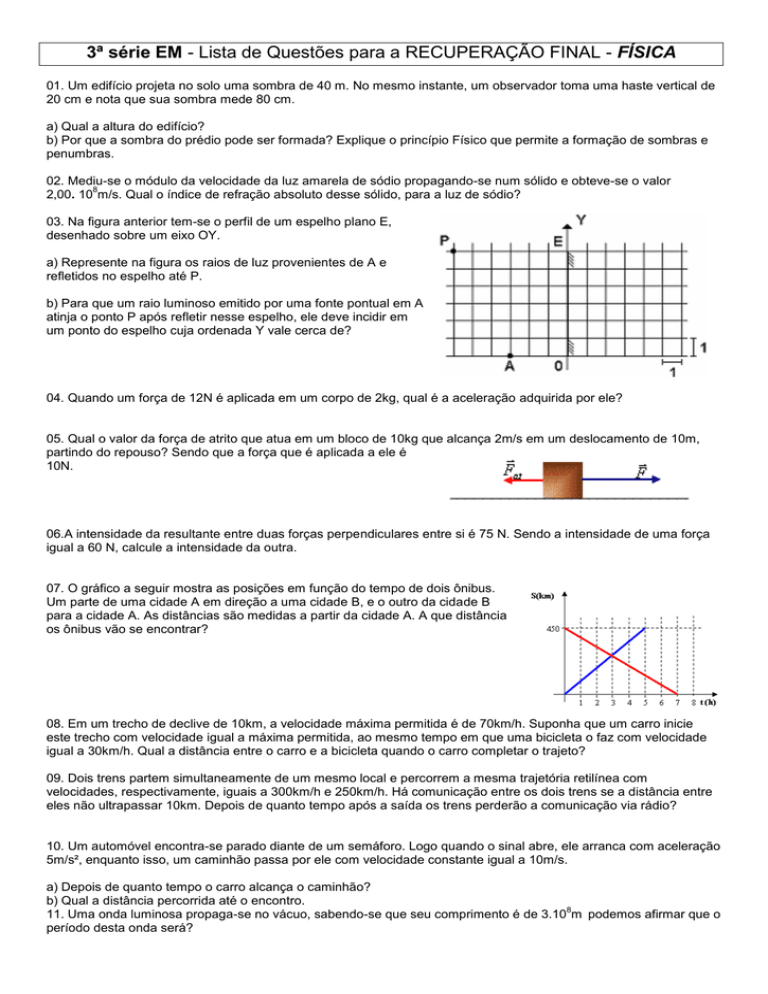
17. Uma barra (20 m) de massa 200 kg é apoiada nas suas
extremidades por suportes A e B. Uma pessoa começa a
andar pela barra. Sabendo que a pessoa possui massa de
55 kg, determine a força no suporte A para manter a barra
em equilíbrio quando a pessoa está a 5 m da extremidade A.
2
Adote g = 10m/s .
18. Um corpo é lançado horizontalmente do alto de um prédio de 20 m de altura e atinge o solo a uma distância de 60
2
medidos na horizontal a partir do ponto de lançamento. Adotando-se g= 10 m/s .
Determine a velocidade inicial de lançamento. Desprezando-se a resistência do ar.
19. Calcular o alcance de um projétil lançado por um morteiro com velocidade inicial de 100 m/s, sabendo-se que o
ângulo formado entre o morteiro e a horizontal é de 30º. Adotar g = 10 m/s2 .
Dado sen30º = 0,50 e cos 30º = 0,87
20. A barra da figura é um corpo rígido de peso desprezível,
apoiada no ponto P. Qual o módulo da força que mantém a barra
em equilíbrio mecânico na posição horizontal?
21. Um bloco de ferro de 10cm³ é resfriado de 300°C para 0°C. Quantas calorias o bloco perde para o ambiente?
Dados: densidade do ferro=7,85g/cm³ e calor específico do ferro=0,11cal/g.°C
22. Qual a quantidade de calor absorvida para que 1L d'água congelado e à -20°C vaporize e chegue a temperatura
de 130°C.
Dados:
Calor latente de fusão da água: L=80cal/g
Calor latente de vaporização da água: L=540cal/g
Calor específico do gelo: c=0,5cal/g.°C
Calor específico da água: c=1cal/g.°C
Calor específico da água: c=0,48cal/g.°C
Densidade da água: d:1g/cm³
1L=1dm³=1000cm³
23. As cargas Q e q estão separadas pela distância (2d) e se repelem com força (F). Calcule a intensidade da nova
força de repulsão (F') se a distância for reduzida à metade e dobrada a carga Q.
24. Duas cargas elétricas positivas Q1 e Q2 interagem-se, no vácuo, através de
uma força elétrica cuja intensidade varia com a distância entre elas, de acordo
9
2
2
com o gráfico abaixo. Considerando K=9.10 N.m /C e que o valor da carga Q2
é quatro vezes maior do que Q1, determine o valor de Q2.
25. Duas esferas igualmente carregadas, no vácuo, repelem-se mutuamente quando separadas a uma certa
distância. Triplicando a distância entre as esferas, a força de repulsão entre elas torna-se:
a) 3 vezes menor
b) 6 vezes menor
c) 9 vezes menor
d) 12 vezes menor
e) 9 vezes maior
Justifique a sua escolha.
26. O campo elétrico gerado em P, por uma carga puntiforme positiva de valor +Q a uma distância d, tem valor
absoluto E. Determinar o valor absoluto do campo gerado em P por outra carga pontual positiva de valor +2Q a uma
distância 3d, em função de E.
27. A velocidade da Terra ao passar pelo periélio em torno do sol é:
a) Máxima
b) Diminuída
c) Constante como em toda trajetória
d) O movimento da Terra é desacelerado
e) o quádruplo do valor de sua distancia
28. Um satélite da Terra move-se numa órbita circular, cujo raio é 4 vezes maior que o raio da órbita circular de outro
satélite. Qual a relação T1/T2, entre os períodos do primeiro e do segundo satélite?
a) 1/4
b) 4
c) 8
d) 64
e) não podemos calcular a razão T 1/T2, por insuficiência de dados.
29. Considere um corpo A de massa 20kg. Para que este corpo atraia o planeta Terra com uma força de 50N, sua
distância à superfície terrestre deve ser aproximadamente igual:
a) ao raio da Terra;
b) ao dobro do raio da Terra;
c) ao quádruplo do raio da Terra;
d) à metade do raio da Terra;
e) a um quarto do raio da Terra.
o
o
30. O calor específico de uma substancia é 0,5 cal/g C. Se a temperatura de 4 g dessa substancia se eleva de 10 C,
a) pode-se afirmar que ela absorveu uma quantidade de calor, em calorias, de?
b) A Capacidade térmica do corpo em cal/ºC é?
31. Se R é o raio médio da órbita de um planeta X, e T é o seu período de revolução em torno do Sol, a 3º lei de
2
3
Kepler estabelece que T =C.R , onde C é uma constante de proporcionalidade, válida para todos os planetas de
nosso sistema solar. Suponha que a distância média do planeta X ao Sol é 4 vezes a distância média da Terra ao
Sol. Determine o período do planeta X em anos.
32. Observe o circuito, representado abaixo, onde encontramos três lâmpadas
idênticas ligadas a uma pilha comum, por meio de fios ideais. Responda as
questões que seguem:
a) Se a lâmpada B se queimar o que acontecerá com as lâmpadas A e C? Por
quê?
b) Com as três lâmpadas acesas, o que acontecerá com o brilho das lâmpadas B e
C, se provocarmos um curto-circuito na lâmpada A? Por quê?
33. Considere um planeta que tenha raio e massa duas vezes maiores que os da Terra. Sendo a aceleração da
2
gravidade na superfície da Terra igual a 10m/s , qual será a gravidade na superfície deste planeta?
34. Um corpo de massa m=4 kg encontra-se em um planeta cujo raio é metade do valor do raio da Terra. Qual o
valor da força entre esse corpo e o planeta?
35. Determine a resistência elétrica equivalente do circuito ao
lado.
20Ω
10Ω
4Ω
4Ω
8Ω
36. A ddp entre os pontos A e B do trecho do circuito elétrico
abaixo é 80 V. Determine a corrente elétrica que atravessa o
resistor de resistência elétrica igual a 7Ω.
37. Temos três resistores elétricos de intensidade 4Ω, 6Ω e 2Ω e uma fonte de tensão que pode fornecer uma ddp de
36V. Determine:
a) A corrente elétrica que passa pelo resistor de 6Ω quando os três resistores estão em paralelo, ligados a fonte de
tensão.
b) A corrente elétrica que passa pelo resistor de 2Ω quando os três resistores estão em série e ligados à fonte de
tensão.
38. Devido à resistência do ar, as gotas de chuva caem com velocidade constante a partir de certa altura. O módulo
2
-6
2
da força resistiva do ar é dado por F= k.v , onde k é uma constante de valor 8 x 10 N/(m/s) e v é o módulo da
-7
velocidade. Nessas circunstâncias, uma gota cujo módulo do peso vale 3,2x10 N atinge o solo com velocidade de
módulo, em m/s, de?
39. Abandona-se, de uma altura muito grande, um objeto de massa m, que então cai verticalmente. O atrito com o ar
não é desprezível; sobre o objeto atua uma força resistiva proporcional ao quadrado da velocidade, que em módulo
2
2
vale Fr=K.V . Dados: m=4,0kg; K=2,5kg/m; g=10m/s .
Depois de um longo tempo o objeto atinge velocidade constante. Calcule o valor dessa velocidade.
40. Em um salto de paraquedismo, identificam-se duas fases no movimento de queda do paraquedista. Nos primeiros
instantes do movimento, ele é acelerado. Mas devido à força de resistência do ar, o seu movimento passa
rapidamente a ser uniforme com velocidade v1, com o paraquedas ainda fechado. A segunda fase tem início no
momento em que o paraquedas é aberto. Rapidamente, ele entra novamente em um regime de movimento uniforme,
com velocidade v2. Supondo que a densidade do ar é constante, a força de resistência do ar sobre um corpo é
2
proporcional à área sobre a qual atua a força e ao quadrado de sua velocidade F= k.v . Determine a razão V2/V1
sabendo que a área efetiva aumenta 100 vezes no momento em que o paraquedas se abre.