G3 – FIS1026 – 14/06/2012 MECÂNICA NEWTONIANA B NOME

G3 – FIS1026 – 14/06/2012
MECÂNICA NEWTONIANA B
NOME:___________________________________________________
Matrícula: ___________________
QUESTÃO
VALOR
1
3,5
2
3,5
3
3,0
Total
10,0
TURMA:_______
GRAU
REVISÃO
Sistema de
coordenadas
y
Dados:
g = 10 m/s2;
α constante: Δω = αt; Δθ = ω0 t + ½ αt2; ω2= ω02 + 2αΔθ;
z
τ = r × F; Στ = Iα;
x
I = Σ miri2; at = αr; vt = ωr; Ip = Icm + Md2;
Icm = β MR2; βaro = 1; βcilindro/disco = 1/2; βesfera sólida= 2/5; Icm haste = 1/12 ML2;
L = r × p; L = I ω ; Στ ext = dL/dt ;
sen 30o = 0,50 ; cos 30o = 0,86.
A duração da prova é de 1 hora e 50 minutos.
NÃO SERÃO ACEITAS RESPOSTAS SEM JUSTIFICATIVAS E CÁLCULOS
EXPLÍCITOS
Não é permitido destacar folhas deste caderno de respostas.
A prova só poderá ser feita a lápis, caneta azul ou preta
É permitido o uso de calculadoras científicas simples.
Não é permitido o uso de aparelhos celulares.
G3 – FIS1026 – 14/06/2012
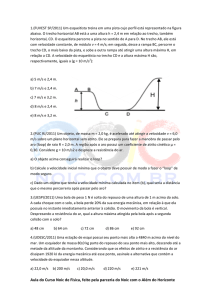
1ª QUESTÃO (3,5 pontos)
Considere o sistema ao lado,
onde um cilindro maciço de
massa 2M e raio 2R pode girar
sem atrito em torno de um eixo
vertical fixo à superfície, que
passa pelo seu centro de massa.
Uma corda ideal e de massa
desprezível está enrolada em
torno do cilindro, passa por
uma polia em forma de aro
com massa M e raio R e está
presa a um bloco de massa desconhecida. Não há atrito nos eixos da rotação da polia e do
cilindro e não ocorre escorregamento da corda no cilindro ou na polia. Tampouco há atrito
entre o bloco e a superfície do plano inclinado. O raio R da polia (aro) vale 10 cm e o ângulo
θ é 30o . Observa-se que o bloco desce com uma aceleração linear a = 0,1 m/s2.
(a) [1,0] Havendo o sistema partido do repouso, observa-se que a polia sofre um
deslocamento angular total de 50 radianos até que o bloco chegue à base da rampa.
Determine o tempo de queda do bloco, Δt, e a velocidade angular final do cilindro
maciço, ωcil.
(b) [0,6] Faça o diagrama do corpo livre para cada componente do sistema, representando
claramente as forças que agem em cada um dos componentes e o sentido de seus
movimentos (de translação ou rotação).
(c) [0,9] Escreva as equações resultantes das Leis de Newton (rotacional e translacional) para
os três corpos.
(d) [1,0] A partir das equações da letra (c), determine o valor da massa do bloco, em termos
de M.
2ª QUESTÃO (3,5 pontos)
Um disco de raio r e massa M desce
sem deslizar, a partir do repouso, a
rampa inclinada conforme a figura.
Após chegar à base da rampa AB, ele
segue na horizontal para a pista em
forma de circunferência com raio R e
sobe essa pista rolando sem deslizar.
O ângulo entre a rampa e a horizontal é θ = 30º. O raio do disco r vale r = R/10 e o
comprimento (D) da rampa, do ponto A ao ponto B, vale D = 8R, onde R é o raio da pista
circular. A aceleração da gravidade local é g. A linha tracejada corresponde a uma possível
trajetória do centro de massa (CM) do disco.
(a) [1,0] Faça o diagrama de forças para o disco durante o percurso de A até B. A partir das
leis sobre torque e força, obtenha uma expressão literal, em função de g, para o valor da
aceleração do CM (aCM) do disco entre A e B. Use o sistema de coordenadas desenhado na
figura.
(b) [0,7] Indique claramente o sentido da força de atrito estática (fE) feita pela superfície da
rampa sobre o disco. Determine uma expressão literal para fE, em função de M e g. Resolva
através da segunda lei de Newton aplicada ao centro de massa do disco.
(c) [1,0] Encontre uma expressão literal para o valor da velocidade angular do disco (ωB) em
torno de um eixo horizontal que passe em seu CM, quando o disco chega ao ponto B, em
função de g e R. Resolva através do uso de leis físicas referentes à energia mecânica.
(d) [0,8] O valor mínimo da velocidade do CM do disco para passar no ponto mais alto da
!"#
pista circular (C), sem perder o contato com a pista, é !!"
= ! ! − ! =
!
!"
!".
Obtenha uma expressão literal para a velocidade do CM do disco no ponto C, vCM, em
função de g e R através de leis físicas sobre a energia mecânica. Compare com o valor
mínimo dado e diga se o disco passará pelo ponto C em contato com a pista ou se descolará
dela antes de chegar a C.
3ª QUESTÃO (3,0 pontos)
Um aro uniforme de raio r = 0,2m e massa M =1,0 kg está preso
a um fio de massa desprezível e está girando em uma superfície
horizontal. Na figura ao lado, a trajetória do centro de massa do
aro está indicada pela circunferência tracejada. A trajetória tem
raio R1 =1,0 m e a velocidade angular do aro é ω1 = 2 rad/s.
Suponha inicialmente que não há atrito entre o aro e a superfície.
(a) [0,5] Escreva o modulo do momento angular L1 do aro em
relação ao centro da trajetória.
(b) [1,0] Um dispositivo oculto no centro da trajetória diminui o raio para R2 = 80 cm. Neste
novo raio, qual é o novo valor da velocidade angular ω2? Justifique claramente o conceito
físico utilizado.
(c) [0,5] Encontre o trabalho realizado pelo dispositivo oculto da letra (b).
(d) [1,0] Suponha agora que há atrito entre o aro e a superfície. Se no instante t = 0 o aro
está girando na circunferência de raio R1 (original) e com velocidade angular ω3 = 4 rad/s, e
que o coeficiente de atrito estático é 0,4 e o de atrito cinético é 0,3, calcule o intervalo de
tempo que o aro demora em parar totalmente.
1ª QUESTÃO
(a)
(b)
(c)
(d)
2ª QUESTÃO
(a)
!!" = !! !

!!" + !!" + !!" = !! ! ,
onde escolhemos um ponto G de contato entre o disco e a rampa como o ponto de referência para o cálculo dos
torques. Como os pontos de aplicação das forças normal ! e de atrito estático !! coincidem com o ponto G,
seus torques valem zero e temos:
!!" = !! ! onde !!" e ! apontam para dentro da folha ao longo do eixo z. Como !!" = !"#$%&, vem:
!"#$%& = !! !
(1).
!
!
!!"
!
!
!
Substituindo ! = !", !! = !!" + !! ! = !! ! + !! ! = !! ! e ! = !
!
!
!
em (1) temos:
!"#!"#$ = !! ! !"  !!" = !"#$% = !.
!
!
!
!
Obs: o problema pode ser resolvido também escolhendo o CM do disco como referência para o torque. O
resultado para fE será o mesmo.
(b)
!! = !!!"
 !"#$% − f! = !!!"  f! = !"#$% − !!!" 
!
!
!
!
!
!
f! = !"#$%& − ! !"#$%  !! = !"#$%& = !".
(c) As forças não conservativas (Normal e Força de Atrito Estática) não realizam trabalho ao
longo da descida da rampa. Vale a conservação da energia mecânica:
!!" = !!"
!! + !! = !! + !!

!
!
!
!
!"#$%&' = !!!" ! + !!" !! ! ,

!
onde !"#$% é a altura entre as posições do CM do disco nos pontos A e B. Usando !!" = !! ! , !!" = !!!
!
na expressão anterior vem:
!
!
!
!
!"#$%&' = !! ! (!! ! + !! ! )
!
!
!
!! !
 2!"#$%& = ! ! ! !  !! ! = !! = !
!!!
!"!"#$ ou !! = !"
!
!"
!"!"#$ 
.
(d) As forças não conservativas (Normal e Força de Atrito Estática) não realizam trabalho entre
os pontos A e C. Vale a conservação da energia mecânica:
!
!
!!" = !!"  !! + !! = !! + !!  !"#$%&' = !" 2! − 2! + !!!" ! + !!" !! ! ,
!
!
!
!
!"
onde !!" = !! ! . Usando !!" = !!! , ! = 8!, ! =
!
!
! !
!
!
! !
!"#4 = !"# + !!!" ! + !!
!
!! !
!
!
, !"#$ = , temos:
!!" !
!!
!

!
!!
!
!"
!" = !!" !  !!" ! (!) = 4−
!
!
!
!
!
!
!"# = !!" ! ! + !
!" > !!"#í! ! =
!
!"

!".
Conclui-se que o disco passará pelo ponto mais alto da pista circular sem descolar dela.
3ª QUESTÃO
(a) Neste caso, L = Iω. O momento de inércia tem que ser calculado usando o teorema dos
eixos paralelos I = ICM + MR2 = Mr2 + MR12 = M(r2 + R12). Assim,
L1 = M(r2 + R12)ω1 = 1 (0,22 + 12)*2 = 2,08 kg*m2/s
b) Neste caso, as forças fazendo torque são o peso e a normal, porem a soma destes dois
torques é nula. Assim, o momento angular é conservado durante todo o processo:
L1 = L2  M(r2 + R12) ω = M (r2 + R22) ω2  ω2 = ω1 (r2 + R12) / (r2 + R22) = 2*(0,22 +
12)/(0,22 + 0,82) = 2 * 1,04/0,68 = 3,06 rad/s
1
c) A única força que faz trabalho neste processo é a força de tração no arame. Assim, pelo
teorema trabalho-energia:
WT = KF – KI = ½ IFωF2 - ½ IIωI2 = 0,5*0,68*3,062 – 0,5*1,04*22 = 3,18 – 2,08 = 1,1 J
d) Como a força de atrito que age é o atrito cinético, ele é constante e vai produzir um torque
constante. Assim: τ= dL/dt = ΔL/Δt = (Lf - Li) /Δt  Δt = (Lf – Li)/τ.
Como o aro vai parar no final  Lf = 0. A força de atrito cinética vai produzir um torque
contrario ao movimento de giro do aro, pelo qual o torque dele é negativo  τ= -R1*Fat = R1µcinMg; e Li = M(r2 + R12)ω3
Assim: Δt = - M(r2 + R12)ω3 / (-R1µcinMg) = 1*(0,22 + 12)*4/(1*0,3*1*9,8)=4,16/2,94 = 1,41