cap1.

Introdução
A teoria das probabilidades é um ramo da matemática que lida modelos de fenômenos aleatórios. Intimamente relacionado com a teoria de probabilidade está a Estatística, que se preocupa com a criação de princípios, métodos e critérios a fim de tratar dados relativos fenômenos
aleatórios ou dados experimentais e outras observações do mundo real.
A teoria de probabilidade teve inicio com os jogos de azar no seculo XVI, mas sua teoria
axiomática, só veio em 1930 com o matemático soviético Kolmogorov. A teoria elementar da
probabilidade é baseada na teoria de conjuntos.
Na natureza é comum encontrarmos situações que envolvem um elemento de incerteza, ou
aleatoriedade. Essas situações são denominadas fenômenos ou experimentos aleatórios. Os
modelos de probabilidade, visam descrever experimentos aleatórios, isto é, experimentos que
podem ser repetidos (indefinidamente) e onde os resultados futuros não pode ser exatamente
previsto, devido à aleatoriedade, mesmo que o experimento seja totalmente controlado.
A fundação de estatísticas encontra-se na ideia de um experimento aleatório. Um experimento é chamado aleatório se seu resultado não pode ser predito precisamente porque as
condições em que é realizado não podem ser predeterminadas com precisão suficiente.
Exemplos:
Joga-se um dado e observa-se o número obtido na face superior. Resultados possíveis
1, 2, 3, 4, 5, 6
Um lote de 10 peças contém 3 defeituosas. As peças são retiradas uma a uma (sem reposição) até que a última defeituosa seja encontrada. Conta-se o número de peças retiradas.
Resultados possíveis 3, 4, 5, 6, 7, 8, 9, 10
Uma lâmpada nova é ligada e observa-se o tempo gasto até queimar. Resultados possíveis
[0, ∞)
1
TEORIA DE CONJUNTOS
Um conjunto é qualquer coleção bem definida de objetos, chamados elementos. São exemplos de conjuntos:
• O conjunto de todos os números inteiros,
• O conjunto de todos os alunos da UFMT
• O conjunto de todos os seres humanos vivos atualmente,
• O conjunto de todos os números reais maiores que zero e menores que 1,
• O conjunto de todos os jogadores da atual seleção
• O conjunto de todas as letras do alfabeto romano.
Conjuntos são representados por letras maiúsculas: A, B, C, S, e os elementos de um conjunto são representados por letras minúsculas: a, b, x, y.. Em geral, podemos especificar um
conjunto descrevendo os seus elementos por meio de uma condição ou então enumerando os
seus elementos.
Exemplo 1.1: Seja A o conjunto de todos o números inteiros maior que 5. Este conjunto
pode ser representado por:
A = {x ∈ N|x > 5}
onde se lê: x pertence ao conjunto dos numero naturais tal que x seja maior que 5.
Exemplo 1.2: Seja B o conjunto de todos as cores da bandeira do Brasil.
B = {verde, amarelo, azul, branco}
Podemos definir um conjunto de diversas formas. Se um conjunto tem poucos elementos,
podemos listá-los, um a um, em qualquer ordem, entre chaves. Por exemplo, o conjunto cujos
elementos são os números inteiros 2, 3 e 5 pode ser escrito A = {2, 3, 5}. Assim, por exemplo,
temos que 3 ∈ A, mas 4 6∈ A.
Existem alguns conjuntos de números que são muito usados em matemática, e tem notações
convencionais bem estabelecidas:
Teoria de Conjuntos
3
• o conjunto dos números naturais N = {0, 1, 2, 3, 4, ...}
• o conjunto dos números inteiros Z = {..., −4, −3, −2, −1, 0, 1, 2, 3, 4, ...}
• o conjunto dos números racionais Q = {x = ab /a, b ∈ Z e b > 0}
• o conjunto dos números irracionais I = {x|x 6∈ Q}
• o conjunto dos números reais R = {x|x ∈ Q ou x ∈ I}
Definição 1.1: O Espaço Amostral, representado por Ω, é o conjunto de todos os resultados
possíveis de um experimento aleatório.
Exemplo 1.3: Joga-se uma moeda 4 vezes e o observa-se o número de caras obtido. Ω =
(0, 1, 2, 3, 4).
• 0 - 1 possibilidade (Co,Co,Co,Co);
• 1 - 4 possibilidades (Co,Co,Co,Ca); (Co,Co,Ca,Co); (Co,Ca,Co,Co); (Ca,Co,Co,Co);
• 2 - 6 possibilidades (Co,Co,Ca,Ca); (Co,Ca,Co,Ca); (Co,Ca,Ca,Co); (Ca,Co,Co,Ca); (Ca,Co,Ca,Co);
(Ca,Ca,Co,Co)
• 3 - 4 possibilidades (Co,Ca,Ca,Ca); (Ca,Co,Ca,Ca); (Ca,Ca,Co,Ca); (Ca,Ca,Ca,Co);
• 4 - 1 possibilidades (Ca,Ca,Ca,Ca)
Exemplo 1.4: Se o experimento consiste em medir a vida útil de um carro, então um possível espaço amostral consiste de todos os números reais não-negativos, isto é, Ω = [0, ∞)
Definição 1.2: Conjunto vazio, representado por ∅ é o único conjunto que não possui
elementos.
Definição 1.3: Sejam A e B conjuntos. Se todo elemento de A é elemento de B, então A é
chamado um subconjunto de B, ou seja, A ⊂ B, essa representação pode se escrita da seguinte
forma:
A ⊂ B ≡ ∀x[(x ∈ A) → (x ∈ B)]
Definição 1.4: Qualquer subconjunto A do espaço amostral Ω, isto é A ⊂ Ω, ao qual
atribuímos uma probabilidade, é dito um evento aleatório.
1.1
OPERAÇÕES DE CONJUNTOS
Definição 1.5: A união de dois conjuntos quaisquer A e B, denotada por A ∪ B, é o
conjunto dos elementos x tais que x pertence a pelo menos um dos dois conjuntos A e B. Ou
seja:
A ∪ B ⇔ x ∈ A ou x ∈ B
Teoria de Conjuntos
4
Teorema 1.1: Propriedade da União. Sejam X um conjunto e A, B e C subconjuntos de
X. Então temos:
a) O elementos neutro A ∪ ∅ = A
Demonstração. Seja x ∈ A ∪ ∅ ⇔ x ∈ A ou x ∈ ∅ ⇔ x ∈ A. Logo A ∪ ∅ = A
b) Lei de idempotência A ∪ A = A
Demonstração. Seja x ∈ A ∪ A ⇔ x ∈ A ou x ∈ A ⇔ x ∈ A. Logo A ∪ A = A
c) Lei comutativa A ∪ B = B ∪ A
Demonstração. Seja x ∈ A ∪ B. Então por definição de união x ∈ A ou x ∈ B,o que é
equivalente a x ∈ B ou x ∈ A, assim, A ∪ B = B ∪ A
d) Lei associativa A ∪ (B ∪ C) = (A ∪ B) ∪ C
Demonstração. Seja x ∈ A∪(B ∪C) ⇔ x ∈ A ou x ∈ (B ∪C), e x ∈ (B ∪C) ⇔ x ∈ B
ou x ∈ C. Assim
x ∈ A ∪ (B ∪ C) ⇔ x ∈ A ou (x ∈ B ou x ∈ C)
x ∈ A ∪ (B ∪ C) ⇔ (x ∈ A ou x ∈ B) ou x ∈ C
x ∈ A ∪ (B ∪ C) ⇔ (x ∈ A ∪ B)ou x ∈ C
x ∈ A ∪ (B ∪ C) ⇔ (x ∈ A ∪ B) ∪ C
Logo A ∪ (B ∪ C) = (A ∪ B) ∪ C
Definição 1.6: A interseção de dois conjuntos quaisquer A e B, denotada por A ∩ B, é o
conjunto dos elementos x tais que x pertence a ambos os conjuntos A e B. Ou seja:
A∩B ⇔x∈A e x∈B
dizemos que A e B são conjuntos disjuntos, se
A∩B =∅
Teorema 1.2: Propriedade da Intersecção Sejam X um conjunto e A, B e C subconjuntos
de X. Então temos:
a) O elementos neutro A ∩ X = A
b) Lei de idempotência A ∩ A = A
c) Lei comutativa A ∩ B = B ∩ A
Teoria de Conjuntos
5
d) Lei associativa A ∩ (B ∩ C) = (A ∩ B) ∩ C
As demonstrações das propriedades da intersecção são análogas a da união.
Teorema 1.3: Leis distributivas. Sejam X um conjunto e A, B e C subconjuntos de X.
Então temos:
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Demonstração. Seja x ∈ A ∩ (B ∪ C) ⇔ x ∈ A e x ∈ (B ∪ C). Assim
x ∈ A ∩ (B ∪ C) ⇔ x ∈ A e (x ∈ B ou x ∈ C)
x ∈ A ∩ (B ∪ C) ⇔ (x ∈ A e x ∈ B) ou (x ∈ A e x ∈ C)
x ∈ A ∩ (B ∪ C) ⇔ (x ∈ A ∩ B) ou (x ∈ A ∩ C)
x ∈ A ∩ (B ∪ C) ⇔ (x ∈ (A ∩ B) ∪ (A ∩ C)
Logo A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
A demostração da segunda parte é análoga.
Definição 1.7: Seja A um de subconjunto Ω o seu complementar, é o conjunto Ac , dos
elementos que não pertencem a A.
Ac = {x ∈ Ω|x 6∈ A}
Teorema 1.4: Seja A um subconjunto de Ω, e Ac o seu complementar. Então temos:
• A ∩ Ac = ∅
Demonstração. Seja x ∈ Ω, tal que x ∈ A, por definição se x ∈ A então x 6∈ Ac , logo
não existe um elemento x, tal que x ∈ A e x ∈ Ac , ou seja A ∩ Ac não possui elementos,
e assim A ∩ Ac = ∅.
• A ∪ Ac = Ω
Demonstração. Por definição temos que se A ⊂ Ω então Ac ⊂ Ω, assim Ω contém todos
os elementos de A e Ac , então não existe um elemento de Ω que não pertença a A ou Ac ,
logo A ∪ Ac = Ω.
Teoria de Conjuntos
6
Definição 1.8: Sejam dois conjuntos quaisquer A e B,a diferença de A \ B ou A − B,é o
conjunto dos elementos que pertencem a A e que não pertencem a B.
A − B = {x ∈ A|x 6∈ B} = A ∩ B c
Exemplo 1.5: Seja Ω = {(x, y) ∈ R|0 ≤ x ≤ 1, e 0 ≤ y ≤ 1}
Sejam os subconjuntos de Ω
• A1 = {(x, y) ∈ R|0 ≤ x ≤ 1, e 0 ≤ y ≤ 12 }
• A2 = {(x, y) ∈ R|0 ≤ x ≤ 12 , e 0 ≤ y ≤ 1}
• A3 = {(x, y) ∈ R|0 ≤ x ≤ 21 , e 0 ≤ y ≤ 21 }
• A4 = {(x, y) ∈ R|0 ≤ x ≤ y ≤ 1}
Pode-se verificar as relações nos subconjuntos:
• A3 ⊂ A1
• A3 ⊂ A2
Teoria de Conjuntos
7
• A3 ⊂ A4
• A1 ∩ A2 = A3
• Ac3 = {(x, y) ∈ R|0 ≤ x ≤ 1 se
1
2
<y≤1e
1
2
≤ x ≤ 1 se 0 < y ≤ 12 }
• A1 ∪ Ac3 = Ω
• Ac1 = {(x, y)|0 ≤ x ≤ 1, e
1
2
< y ≤ 1}
Teorema 1.5 (Lei de De Morgan Generalizada): Teorema de De Morgan: Seja {A1 , A2 , ..., An }
uma coleção de subconjuntos de Ωu. Então
!c
n
n
[
\
a)
Ai =
Aci
i
n
\
b)
i
!c
Ai
=
n
[
i
Aci
i
n
[
Demonstração. Prova parte a) (⇒) Seja x ∈
Assim, x ∈ Aci , ∀i, logo x ∈
(⇐) Seja x ∈
assim, x ∈
n
[
n
\
n
\
i
!c
Ai
. Então x 6∈
n
[
Ai , ou seja, x 6∈ Ai , ∀i.
i
Aci .
i
Aci . Então x ∈ Aci , ∀i, e ainda x 6∈ Ai , ∀i. Dessa forma x 6∈
n
[
Ai , e
i
!i c
Ai
i
Demonstração. Prova parte!b)
c
n
n
\
\
(⇒) Seja x ∈
Ai . Então x 6∈
Ai , ou seja, para algum i x 6∈ Ai , isto é, x 6∈
i
i
A1 ou x 6∈ A2 ou , ..., ou x 6∈ An , então x ∈ Ac1 ou x ∈ Ac2 ou , ..., ou x ∈ Acn . Dessa forma
n
[
x∈
Aci
i
(⇐) Seja x ∈
n
[
Aci . Então para algum i x ∈ Aci , isto é, x ∈ Ac1 ou x ∈ Ac2 ou , ..., ou x ∈
i
Acn ,
então, x 6∈ A1 ou x 6∈ A2 ou , ..., ou x 6∈ An . Dessa forma, x 6∈
!c
n
\
Ai .
n
\
Ai , logo, x ∈
i
i
Vale ressaltar que as Leis de Morgan também são válidas para o caso em que n = ∞
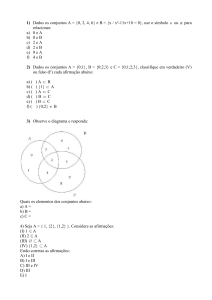
Exemplo 1.6: Seja A1 , A2 , A3 subconjuntos de Ω, podemos indicar as operações como pelo
diagram de Venn.
Teoria de Conjuntos
1.2
8
CLASSES DE CONJUNTOS
Definição 1.9: Uma classe de conjuntos ou coleção de conjuntos é um conjunto cujos elementos são subconjuntos de um dado espaço. São usados geralmente quando queremos tratar
de alguns subconjuntos de um dado conjunto. Uma coleção de conjuntos pode ser denotada
por letras caligráficas maiúsculas A; B; C
Definição 1.10: Uma classe A de subconjuntos de Ω é chamada de álgebra se
1. Ω ∈ A
2. Se A ∈ A então Ac ∈ A (a classe é fechada pela complementariedade)
3. Se A1 , A2 , ..., An ∈ A então
n
[
Ai ∈ A (a classe é fechada pela união finita)
i
Definição 1.11: Uma classe A de subconjuntos de Ω é chamada de σ-álgebra se
1. Ω ∈ A
2. Se A ∈ A então Ac ∈ A
3. Se A1 , A2 , ... ∈ A então
∞
[
Ai ∈ A
i
Proposição 1.1: Se A é uma σ-álgebra de subconjuntos de Ω. Então:
Teoria de Conjuntos
9
1. ∅ ∈ A
2. Se A1 , A2 , ... ∈ A então
∞
\
Ai ∈ A
i
Demonstração. .
Parte 1)
A é uma σ-álgebra então Ω ∈ A e Ωc = ∅ ∈ A.
Parte 2)
∞
[
c
c
Aci ∈ A. Então
Se A1 , A2 , ... ∈ A, então A1 , A2 , ..., ∈ A, assim
classe é fechada pela complementariedade
∞
\
i
∞
\
!c
Ai
∈ A, como a
i
Ai ∈ A
i
Exemplo 1.7: Seja a coleção A = {∅, Ω} , verifique se é uma σ-álgebra.
1. Ω ∈ A
2. Ω ∈ A, temos que Ωc = ∅ ∈ A
3. ∅, Ω ∈ A então ∅ ∪ Ω = Ω ∈ A
Como as três propriedades são satisfeitas logo A é uma σ-álgebra.
Exemplo 1.8: Sejam A, B, C subconjuntos não vazios de Ω, disjuntos, e tais que
A∪B∪C =Ω
Seja a coleção A = {∅, A, B, C, A ∪ B, A ∪ C, B ∪ C, Ω} , verifique se é uma σ-álgebra.
1. Ω ∈ A
2. Os complementares dos elementos de A está em A
∅c = Ω, Ωc = ∅, Ac = B ∪ C, B c = A ∪ C,
C c = A ∪ B, (A ∪ B)c = C, (A ∪ C)c = B, (B ∪ C)c = A
3. As uniões de todos os elementos de A está em A
A união do ∅ dá os próprios elementos;
A união de Ω com qualquer elemento da o próprio Ω;
A ∪ B, A ∪ C, A ∪ (A ∪ B) = (A ∪ B), A ∪ (A ∪ C) = (A ∪ C), A ∪ (B ∪ C) = Ω ∈ A
B ∪ A, B ∪ C, B ∪ (A ∪ B) = (A ∪ B), B ∪ (A ∪ C) = Ω, B ∪ (B ∪ C) = (B ∪ C) ∈ A
C ∪ A, C ∪ B, C ∪ (A ∪ B) = Ω, C ∪ (A ∪ C) = (A ∪ C), C ∪ (B ∪ C) = (B ∪ C) ∈ A
Teoria de Conjuntos
10
Como as três propriedades são satisfeitas logo A é uma σ-álgebra.
Exemplo 1.9: Seja Ω = {1, 2, 3} e A = {∅, {1}, {2}, {1, 3}, {2, 3}, Ω}, verifique se A é
uma σ-álgebra.
1. Ω ∈ A
2. Os complementares dos elementos de A está em A
∅c = Ω, Ωc = ∅, {1}c = {2, 3}, {2}c = {1, 3}, {1, 3}c = {2}, {2, 3}c = {1}
3. As uniões de todos os elementos de A está em A
A união do ∅ dá os próprios elementos;
A união de Ω com qualquer elemento da o próprio Ω;
{1} ∪ {2} = {1, 2} 6∈ A
Como a terceira propriedade não é satisfeita, logo A não é uma σ-álgebra.
Definição 1.12: Seja Ω um conjunto com uma σ-algebra associada, A, então o par (Ω, A)
é chamado de espaço mensurável.
Definição 1.13: Se Ω = R um conjunto com uma σ-algebra associada, R, então o par
(R, R) é chamado de espaço de Borel. A σ-algebra de Borel, ou Borel-σ-algebra, é definida
como a σ-algebra gerada por conjuntos abertos de R. Os elementos de R são chamados de
bolerianos.
São borelianos todos os tipos de intervalo. Comecemos com os intervalos do tipo
{x ∈ R|x < c}
Pela segunda propriedade da definição de σ-álgebra temos:
{x ∈ R|x < c} ∈ R ⇒ {x ∈ R|x ≥ c} ∈ R
Pela terceira propriedade da definição de σ-álgebra temos:
∞ X
1
∈R
{x ∈ R|x < c} =
x ∈ R|x ≤ c −
n
n=1
Teoria de Conjuntos
11
Como interseções de elementos de R pertencem à R , podemos escrever
(a, b] = {x ∈ R|x > a} ∩ {x ∈ R|x ≤ b} ∈ R
[a, b) = {x ∈ R|x ≥ a} ∩ {x ∈ R|x < b} ∈ R
(a, b) = {x ∈ R|x > a} ∩ {x ∈ R|x < b} ∈ R
[a, b] = {x ∈ R|x ≥ a} ∩ {x ∈ R|x ≤ b} ∈ R
Os subconjuntos unitários pertencem à R, pois {a} = [a, a] ∈ R
1.3
FUNÇÃO INDICADORA
Definição 1.14: Seja Ω um espaço amostral e seja A algum subconjunto de Ω. A função
indicadora de A, denotaa por IA , é uma função com seu dominio em Ω e e contradomínio
binário {0, 1}.
(
1 se ω ∈ A
IA (ω) =
0 se ω 6∈ A
Teorema 1.6 (Propriedades da função indicadora): Seja Ω um espaço amostral e F uma
coleção de subconjuntos de Ω
Exemplo 1.10: Seja a função f definida por





0
x
f (x) =

2−x



0
se
se
se
se
x≤0
0<x≤1
1<x≤2
x>2
Usando uma função indicadora f (x) pode ser escrita da seguinte forma:
f (x) = xI(0,1] (x) + (2 − x)I(1,2] (x)
1. IA (ω) = 1 − IAc (ω) para todo A ∈ F
2. IA1 ∩A2 ∩...∩An (ω) = IA1 (ω)IA2 (ω)...IAn (ω)
3.
1.4
1.4.1
EXERCÍCIOS
Teóricos
1) Demonstre as propriedades da intersecção.
2) Sejam A e B dois subconjuntos não-vazios contidos em um espaço amostral Ω. Mostre que
Teoria de Conjuntos
12
a) A = (Ac ∪ B c )c ∪ (Ac ∪ B)c
b) (A ∪ B) ∩ (A ∩ B)c = (A ∪ B c ) ∪ (Ac ∩ B)
3) Prove que:
a) A ∪ (Ac ∩ B) = A ∪ B
b) A ∪ (A ∩ B) = A
b) (A ∩ B) ∪ (A ∩ B c ) = A
4) Sejam A, B e C conjuntos. Mostre que se A ∪ B = A ∪ C e A ∩ B = A ∩ C. Então B = C
5) Sejam A e B dois conjuntos. Sob que condições o conjunto A ∩ (A ∪ B)c e vazio?
6) Seja Ω um conjunto não-vazio, prove que se A e B são σ-álgebras de subconjunto de Ω,
então A ∩ B também é uma σ-álgebra.
1.4.2
Práticos
1) Sejam A, B e C três eventos em um espaço de probabilidade. Expresse os seguintes eventos
em termos de A, B e C:
a) Apenas A ocorre;
b) A e B ocorrem, mas C não ocorre;
c) Os três eventos ocorrem;
d) Pelo menos um dos três eventos ocorre;
e) Nenhum dos três eventos ocorre;
f) Exatamente um dos três eventos ocorre;
g) No máximo um dos três eventos ocorre;
h) Pelo menos dois dos três eventos ocorrem.
2) Verifique se as relações são verdadeiras:
a) (A ∪ B) ∩ (A ∪ C) = A ∪ (B ∩ C)
b) (A ∪ B) = (A ∩ B c ) ∪ B
c) Ac ∩ B = A ∪ B
d) (A ∪ B)c ∩ C = Ac ∩ B c ∩ C
e) A ∩ B c
Teoria de Conjuntos
13
3) Considere o espaço amostral Ω indicado pelo quadrado definido num sistema de eixos cartesianos de tal forma que 0 ≤ x ≤ 10 e 0 ≤ y ≤ 10. Ilustre graficamente os eventos abaixo:
a) A : x ≤ y
b) B : max(x, y) ≤ 3
c) C : mix(x, y) ≥ 3
d) D : x − y ≤ 3
e) B ∩ C
4)Sejam os conjuntos A = {x ∈ R| − 2 < x < 6} e B = {x ∈ R|x > 3}, determine:
a) A ∩ B
b) A ∪ B
c) A ∪ B c
d) Ac ∩ B
e) A ∩ B c
f) A∪ B c
5) Sejam os conjuntos A = {x ∈ R|1 < x ≤ 2}, B = {x ∈ R| − 2 ≤ x < 4} e C = {x ∈
R| − 1 < x < −1}, determine:
a) (A ∩ B) ∩ C
b) A ∪ (B ∩ C)c
c) (A ∪ C) ∩ B c
d) (Ac ∩ B c )c ∪ C
6) Seja Ω = {1, 2, 3} e A = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, Ω}, verifique se A é uma
σ-álgebra.
7) Seja Ω = {1, 2, 3, 4} e verifique se as coleções de conjuntos abaixo são σ-álgebras.
a) A = {∅, {1}, {2, 3, 4}, Ω},
b) A = {∅, {1, 2}, {3, 4}, Ω},
8) Um curso exigirá 2 provas para aferir o conhecimento do aluno, cuja nota pode variar de 0
a 10. As provas têm peso P1 e P2 e para passar o aluno deve receber nota igual ou superior
a 6. Mostre graficamente o espaço amostral de resultados que o aluno pode receber no curso
e indique o evento "A: o aluno passou no curso", dentro do espaço amostral, considerando 2
casos:
Teoria de Conjuntos
14
a) P1 = 1 e P2 = 1
b) P1 = 1 e P2 = 2
9) Seja Ω = {0, 1, 2, 3} obtenha uma σ-álgebra.
10) Considere Ω = [0, 1] e os seguintes subconjutos:
1
A = {x ∈ Ω|x ≤ }
2
1
B = {x ∈ Ω|x ≥ }
3
Expresse os subconjuntos resultantes das operações abaixo em termos de funções indicadoras
a) (A ∩ B)
b) A ∪ B)
c) (Ac ∪ B)
d) (Ac ∩ B c )