X - Profa. Patricia Maria Bortolon

Estatística I
Aula 7
Prof.: Patricia Maria Bortolon, D. Sc.
MODELOS PROBABILÍSTICOS MAIS
COMUNS
VARIÁVEIS ALEATÓRIAS DISCRETAS
Distribuições de Probabilidade
• Na unidade anterior vimos como descrever uma
distribuição de probabilidade e que características
devem ser obedecidas para que uma função possa
ser característica de uma distribuição de
probabilidades.
• Conhecer a distribuição de probabilidade de um
experimento ou fenômeno nos dá uma forma
simples de avaliar as probabilidades dos resultados
possíveis dos mesmos.
• Os tipos de distribuição podem ser considerados
modelos para descrever situações que envolvem
resultados aleatórios.
Distribuições de Probabilidade
• Cada modelo de distribuição de probabilidades na
estatística, terá seu conjunto de hipóteses que
definem as condições sob as quais aquele modelo
pode ser utilizado validamente.
• Os objetivos destas duas últimas unidades do seu
curso podem ser resumidos nas duas seguintes
questões:
– Que hipóteses ou restrições básicas são exigidas por cada tipo
de distribuição de probabilidades? O conhecimento deste
aspecto é vital para confrontar uma variável aleatória com a
situação real.
– Como se podem usar as distribuições de probabilidades para
obter soluções de problemas?
Distribuições de Probabilidade
• Se a situação real que você analisa se aproxima
fortemente de uma distribuição de probabilidades já
conhecida, sua análise fica muito mais simples,
como veremos adiante.
A essência da análise estatística é confrontar as hipóteses de
uma distribuição de probabilidades com as especificações
de determinado problema.
Distribuições de Probabilidade
• Nesta unidade veremos as principais distribuições
de probabilidade que podem ser aplicadas às
variáveis discretas.
Distribuição Binomial
Distribuição de Poisson
Distribuição Hipergeométria.
Distribuição Binomial:
Propriedades
• A amostra consiste em um número fixo de observações, n
– ex. 15 jogadas de uma moeda; dez lâmpadas retiradas de um
estoque
• Cada observação é classificada como uma de duas
categorias mutuamente excludentes e coletivamente
exaustivas, geralmente chamadas de sucesso e insucesso
– ex. Cara ou coroa em cada jogada da moeda; defeituosa ou não
defeituosa no caso das lâmpadas; ter um menino ou uma menina
– Geralmente chamados “sucesso” e “fracasso”
– Probabilidade de sucesso é p, probabilidade de fracasso é igual a
1–p
• A probabilidade é a mesma para cada observação
– ex. A probabilidade de dar cara é a mesma a cada vez que a
moeda é lançada
Distribuição Binomial:
Propriedades
• As observações são independentes
– O resultado de uma observação não afeta o resultado da
observação seguinte
• Para assegurar essa independência as observações podem
ser selecionadas aleatoriamente, seja a partir de uma
– População infinita sem reposição
– População finita com reposição
Aplicações da Distribuição Binomial
• Uma fábrica que classifica itens como
defeituoso ou não defeituoso
• Uma firma que coloca uma proposta para um
contrato ter sucesso ou não na conclusão do
negócio
• Uma pesquisa de mercado para uma empresa
receber respostas “sim, eu comprarei” ou “não
eu não comprarei” o produto da empresa
• Candidatos a um emprego aceitarem ou não a
oferta da empresa
• Seu time ganhar ou não um jogo de futebol
Distribuição Binomial
Técnicas de Contagem
• Suponha que sucesso seja definido como obter
CARA (C) em pelo menos dois de três lançamentos
de uma moeda equilibrada. De quantas formas esse
“sucesso” pode ocorrer?
• Possibilidades: CCK, CKC, KCC, CCC, logo, há
quatro diferentes maneiras.
• Essa situação é bastante simples. Nós precisamos
de uma forma de contar os sucessos em situações
mais complicadas.
Técnicas de Contagem
Combinações
• Na Aula 4 aprendemos a usar Combinações para
contar de quantas maneiras podemos selecionar X
objetos em um conjunto de n objetos:
n
n!
C(n, X ) =   =
 X  X!(n − X)!
onde:
n! =n(n - 1)(n - 2) . . . (2)(1)
X! = X(X - 1)(X - 2) . . . (2)(1)
0! = 1 (por definição)
Técnicas de Contagem
Combinações
• De quantas formas diferentes podemos escolher 3 sabores de
sorvete se você tem 31 opções de sabores para escolher?
• O total de opções é n = 31, e você escolherá X = 3.
 31
31!
31! 31 • 30 • 29 • 28!
C(31,3) =   =
=
=
= 31 • 5 • 29 = 4495
3 • 2 • 1 • 28!
 3  3!(31 − 3)! 3!28!
Distribuição Binomial
Fórmula
n!
P(X) =
p X (1 − p) n − X
X!(n − X)!
P(X) = probabilidade de X sucessos em n
tentativas, com probabilidade de
sucesso p em cada tentativa
X = no. de ‘sucessos’ na amostra,
(X = 0, 1, 2, ..., n)
n
p
Exemplo: lançar uma
moeda 4 vezes, seja x = #
caras:
n=4
p = 0.5
= tamanho da amostra (numero de
1 - p = (1 - .5) = .5
tentativas ou observações)
X = 0, 1, 2, 3, 4
= probabilidade de “sucesso”
Distribuição Binomial
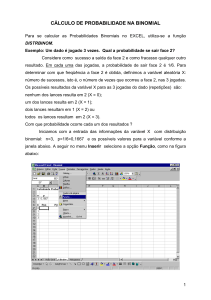
Exemplo
Qual a probabilidade de um sucesso em 5 observações
se a probabilidade de sucesso é 0,10?
X = 1, n = 5, and p = 0,10
n!
p X (1 − p) n − X
X!(n − X)!
5!
=
(0,10)1 (1 − 0,10)5−1
1!(5 − 1)!
P(X = 1) =
= (5)(0,10)(0,90) 4
= 0,32805
Distribuição Binomial
Exemplo
Suponha que a probabilidade de comprar um
computador defeituoso seja de 0,02. Qual a
probabilidade de comprar 2 computadores defeituosos
em um lote de 10 computadores?
X = 2, n = 10, and p = 0,02
n!
p X (1 − p ) n − X
P(X = 2) =
X!(n − X)!
10!
=
(0,02) 2 (1 − 0,02)10− 2
2!(10 − 2)!
= (45)(0,0004)(0,8508)
= 0,01531
Distribuição Binomial
Forma
• A forma da distribuição
binomial depende dos
valores de p e de n
• Aqui, n = 5 e p = 0,10
n = 5 p = 0,10
P(X)
.6
.4
.2
0
0
1
3
4
5
X
5
X
n = 5 p = 0,50
P(X)
• Aqui, n = 5 e p = 0,50
2
.6
.4
.2
0
0
1
2
3
4
Distribuição Binomial
Características
• Média
µ = E(x) = np
• Variância e Desvio Padrão
σ = n p (1 - p )
2
Onde
σ =
n p (1 - p )
n = tamanho da amostra
p = probabilidade de sucesso
(1 – p) = probabilidade de fracasso
Distribuição Binomial
Características
Exemplos
µ = np = (5)(0,10) = 0,5
σ = np (1 - p ) = (5)(0,10)(1 − 0,10)
= 0,6708
n = 5 p = 0,10
P(X)
.6
.4
.2
0
0
1
σ = np(1 - p) = (5)(0,50)(1 − 0,50)
= 1,118
3
4
5
X
5
X
n = 5 p = 0,50
P(X)
µ = n p = (5)(0,50) = 2,5
2
.6
.4
.2
0
0
1
2
3
4
Distribuição Binomial
Exemplo
•
A probabilidade de que uma pessoa fazendo compras num certo
supermercado aproveita uma promoção especial de sorvete é de
0,30. Determine a probabilidade de que dentre seis pessoas
fazendo compras nesse supermercado haja até três aproveitando a
promoção.
– Solução: admitindo que a escolha seja aleatória, substituímos n=6,
p=0,30 e, respectivamente, x=0, 1, 2, 3 na fórmula da distribuição
binomial, otendo:
 6
P (0) =  (0,30) 0 (0,70) 6 = 0,118
 0
6
P (1) =  (0,30)1 (0,70) 5 = 0,303
1
6
P (2) =  (0,30) 2 (0,70) 4 = 0,324
 2
6
P (3) =  (0,30)3 (0,70)3 = 0,185
 3
P ( X ≤ 3) = 0,118 + 0,303 + 0,324 + 0,185 = 0,93
Distribuição de Poisson
Definições
• Muitos estudos são baseados na contagem das
vezes em que um evento específico ocorre em uma
determinada área de oportunidade
• Uma área de oportunidade é uma unidade contínua
ou um intervalo de tempo, volume ou uma área tal
que nela possa acontecer mais de uma ocorrência
de um evento
• Exemplos
– Defeitos na pintura de uma geladeira nova
– Número de falhas na rede em um determinado dia
– Número de pulgas no pêlo de um cachorro
• Nestas situações você usa a distribuição de Poisson
se…
Distribuição de Poisson
Propriedades
A distribuição de Poisson é aplicada quando:
– Você estiver interessado em contar o número de vezes em que um
evento específico ocorre em uma determinada área de
oportunidades. A área de oportunidades é definida pelo tempo,
extensão, área de superfície e assim sucessivamente.
– A probabilidade de que um evento específico ocorra em uma
determinada área de oportunidades é a mesma para todas as áreas
de oportunidades.
– O número de eventos que ocorrem em uma determinada área de
oportunidades é independente do número de eventos que ocorrem
em qualquer outra área de oportunidades.
– A probabilidade de que dois ou mais eventos venham a ocorrer em
uma determinada área de oportunidades se arpoxima de zero à
medida que a área de oportunidades se torna menor.
Distribuição de Poisson
Fórmula
−λ x
e λ
P(X) =
X!
onde:
X = probabilidade de X eventos ocorram numa área de
oportunidade
λ = número esperado de eventos
e = constante matemática aproximada por 2,71828…
Distribuição de Poisson
Parâmetro λ
• O parâmetro λ (a letra grega minúscula lambda), representa a
média, ou o número de sucessos por unidade.
• A variância de uma distribuição de Poisson é igual a λ, e o
desvio padrão é igual a λ
Distribuição de Poisson
Exemplo
• Suponha que, em média, 5 carros entrem em um
estacionamento por minuto. Qual é a probabilidade de que
em um dado minuto, 7 carros entrem?
• Então, X = 7 e λ = 5
−λ x
−5 7
e λ
e 5
P(7) =
=
= 0,104
7!
X!
Portanto, há uma probabilidade de 10,4% de que 7
carros entrem no estacionamento em um dado
minuto.
Distribuição de Poisson
Forma
0.70
λ = 0,50
0.60
0.50
0
1
2
3
4
5
6
7
P(X)
0.6065
0.3033
0.0758
0.0126
0.0016
0.0002
0.0000
0.0000
P(x)
X
0.40
0.30
0.20
0.10
0.00
0
1
2
3
4
x
P(X = 2) = 0,0758
5
6
7
Distribuição de Poisson
Forma
• O formato da distribuição de Poisson depende
do parâmetro λ :
λ = 0,50
λ = 3,00
0.70
0.25
0.60
0.20
0.15
0.40
P(x)
P(x)
0.50
0.30
0.10
0.20
0.05
0.10
0.00
0.00
0
1
2
3
4
x
5
6
7
1
2
3
4
5
6
7
x
8
9
10
11
12
Distribuição de Poisson
Exemplo
• Sabe-se que o número de acidentes de trabalho, por
mês, em uma unidade de produção segue uma
distribuição de Poisson, com uma média aritmética
de 2,5 acidentes de trabalho por mês.
– (a) Qual é a probabilidade de que em um determinado mês
nenhum acidente de trabalho venha a ocorrer?
– (b) De que pelo menos um acidente de trabalho venha a
ocorrer?
Distribuição de Poisson
Exemplo
•
Sabe-se que o número de acidentes de trabalho, por mês, em uma unidade de
produção segue uma distribuição de Poisson, com uma média aritmética de 2,5
acidentes de trabalho por mês.
–
–
•
(a) Qual é a probabilidade de que em um determinado mês nenhum acidente de trabalho
venha a ocorrer?
(b) De que pelo menos um acidente de trabalho venha a ocorrer?
Solução: com λ = 2,5
–
(a)
e −2,5 (2,5) 0
1
P( X = 0) =
=
= 0,0821
2,5
0!
(2,71828) (1)
A probabildade de que em um determinado mês nenhum acidente de trabalho ocorra é 0,0821,
ou 8,21%.
P ( X ≥ 1) = 1 − P ( X = 0) = 1 − 0,0821 = 0,9179
–
(b)
–
A probabilidade de que em um determinado mês haverá pelo menos um acidente de trabalho é
0,9179, ou 91,79%.
A Distribuição Hipergeométrica
• A distribuição binomial é aplicável quando
selecionamos com reposição em uma população
finita ou quando selecionamos sem reposição em
uma população infinita.
• A distribuição hipergeométrica é aplicável quando
selecionamos sem reposição em uma população
finita.
Distribuição Hipergeométrica
• “n” experimentos em uma amostra retirada de
uma população finita de tamanho N
• Amostra retirada sem reposição
• Os resultados não são independentes
• Permite encontrar a probabilidade de “X”
sucessos em uma amostra retirada de uma
população onde há “A” sucessos
Distribuição Hipergeométrica
Fórmula
 A  N − A

 
X  n − X 

P( X ) =
N
 
n 
Onde:
N = tamanho da população
A = número de sucessos na população
N – A = número de fracassos na população
n = tamanho da amostra
X = número de sucessos na amostra
n – X = número de fracassos na amostra
Para entender a fórmula...
• Uma floricultura envia limoeiros de três anos em lotes de 24 e,
quando eles chegam ao destino, um inspetor seleciona ao acaso
três de cada lote. Se essas três árvores são saudáveis, todo o lote
é aceito; caso contrário, as outras 21 árvores do lote também são
inspecionadas. Como um lote pode ser aceito sem inspeção
adicional, mesmo que haja muitas árvores em más condições,
esse procedimento de inspeção envolve um risco considerável.
Para ilustrar a magnitude do risco, vamos supor que, na realidade
6 das 24 árvores estejam em más condições e determinemos a
probabilidade de que um lote inteiro seja, mesmo assim, aceito
sem inspeção adicional. Isso significa que devemos encontrar a
probabilidade de três sucessos (árvores saudáveis) em três
provas (árvores inspecionadas) e poderíamos ser tentados a
argumentar que, como 18 das 24 árvores no lote estão saudáveis,
a probabilidade é de 18/24=3/4 que alguma delas esteja saudável...
Para entender a fórmula...
• ... e portanto a probabilidade procurada é
 3  3 
P ( X = 3) =   
 3  4 
3
0
1
  = 0,42
4
• Esse resultado, obtido com a fórmula da distribuição
binomial, seria correto se a amostragem fosse com
reposição, mas não é isso que ocorre em problemas reais de
inspeção por amostragem. Para obtermos a resposta correta
de nosso problema quando a amostragem é sem reposição,
devemos raciocinar como segue: há um total de  24  = 2.024
3
 
maneiras de escolher três das 24 árvores, e todas elas são
equiprováveis em virtude da hipótese de que a seleção é
aleatória. Entre estas, há 18  = 816 maneiras de selecionar 3
3
 
das 18 árvores saudáveis e decorre, portanto, que a
probabilidade procurada é 816/2.024=0,40.
Para entender a fórmula...
• A expressão da Distribuição Hipergeométrica é uma
generalização do método que usamos no caso das árvores.
• Suponha que devamos escolher n objetos em um conjunto
de N objetos e que neste conjunto de N objetos haja A que
são de um tipo (sucesso) e N-A que sejam de outro tipo
(fracasso), que a amostragem seja sem reposição e que
estejamos interessados na probabilidade de obter X
sucessos e n-X fracassos.
Para entender a fórmula...
• Argumentando como anteriormente, vemos que é possível
escolher n objetos de um conjunto total de N objetos de  N 
 
n
maneiras, e que X dos A sucessos e n-X dos N-A fracassos
podem ser escolhidos de  A  N − A  maneiras. Decorre que,
 X  n − X 
 

na amostragem sem reposição, a probabilidade de “x
sucessos em n provas” é
 A  N − A 
 

X  n − X 

P( X ) =
N
 
n 
Distribuição Hipergeométrica
Características
• A média, ou valor esperado, da distribuição
hipergeométrica é:
nA
µ = E(x) =
N
• O desvio padrão é:
nA(N- A) N - n
⋅
σ=
2
N
N -1
N-n
Onde
N - 1é chamado “Fator de Correção para Populações
Finitas” para amostragens sem reposição de uma população finita.
Distribuição Hipergeométrica
Exemplo
• Computadores são checados em um departamento com 10
computadores. 4 dos 10 computadores tem software ilegal
instalado. Qual é a probabilidade de que ao selecionar três
para checagem, 2 deles tenham softwares ilegais
instalados?
• Então, N = 10, n = 3, A = 4, X = 2
 A  N − A   4  6 
 
   
X  n − X   2 1  (6)(6)

=
P(X = 2) =
=
= 0,30
120
 N
10 
 
 
n 
3 
A probabilidade de que 2 dos 3 computadores selecionados
tenham software ilegal é de 0,30 ou 30%.