laboratório do capítulo 4

Simulação de filtros passivos
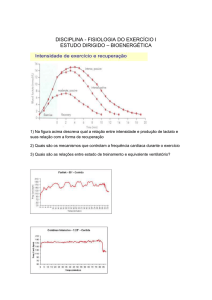
Determinar a resposta em frequência do filtro passivo abaixo utilizando o
matlab:
Procedimento:
a)
b)
c)
d)
Monte a função de transferência do circuito.
Determine o ganho do circuito.
Determine a resposta em frequência uma escala linear.
Determine a resposta em frequência utilizando o diagrama de Bode.
A rotina do MATLAB freqs permite nos avaliar a resposta em frequência
dos circuitos analógicos descritos por equações diferenciais ou funções de
transferências.
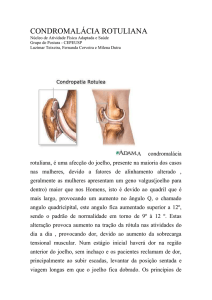
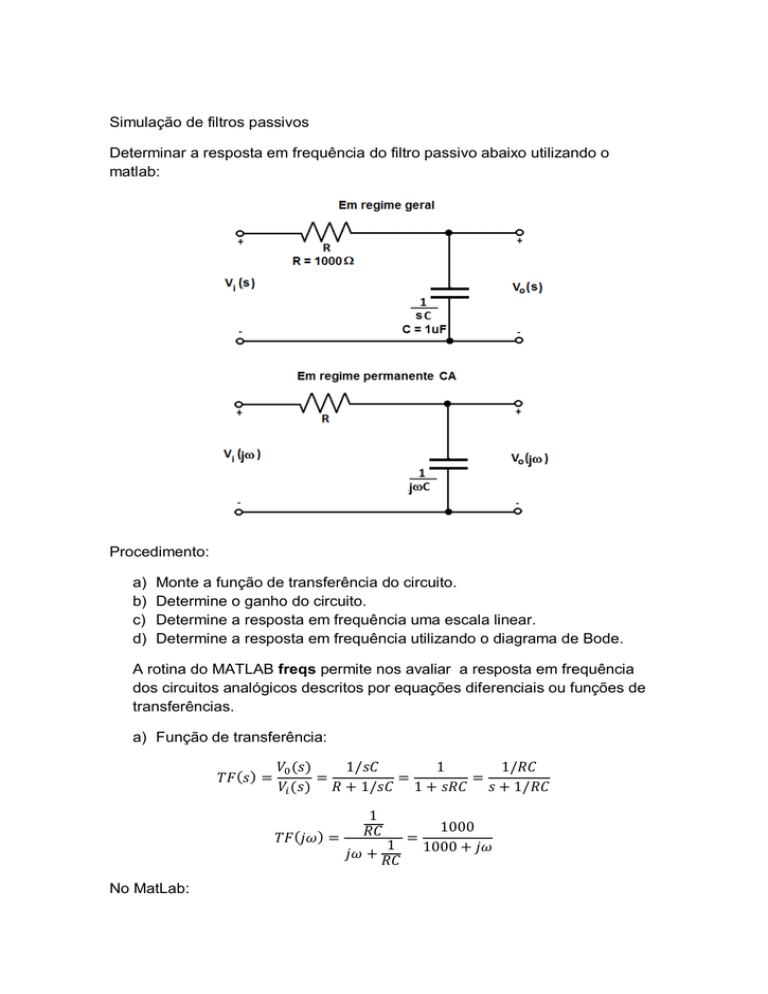
a) Função de transferência:
No MatLab:
A frequência de corte desse circuito é 1/RC=1000 rad/s (159 Hz) de modo que
estabeleceremos uma escala de frequências de 0 a 5000rad/s.
SCRIPT MATLAB
clear all; close all
w=0:1:5000; f=w/(2*pi);
TF1=1000./(1000+j*w);
plot(w,abs(TF1));
xlabel('frequencia angular (rad/s)')
ylabel('Magnitude de TF (undim)')
grid
pause
plot(w,180*angle(TF1)/pi);
xlabel('frequencia angular (rad/s)')
ylabel('Fase de TF1 (graus)')
grid
pause
Modifique o SCRIPT de modo a plotar a magnitude e a fase em função da
frequência em (Hz).
Utilizando o diagrama de Bode:
No caso b0 = 1000, a1 = 1 e a0 = 1000
Monte o SCRIPT MatLab abaixo, na sequência do já montado acima (logo em
baixo).
b0 = 1000;
a0 = 1000;
a1 = 1;
TF2 = tf([b0],[a1 a0]); %tf é a função de transf. do matlab
w = logspace(-1,3);
%gere uma escala de 10-1 a 103
bode(w,TF2);
%plote o diagrama de Bode
grid;
pause
Qual será o valor da tensão de saída se aplicar a tensão de
entrada abaixo no circuito:
Faça os cálculos a mão e obtenha Vo para componente de
frequência e este utilizando o SCRIPT abaixo.
t=0:.0001:0.2;
%gere uma escala (vetor) de tempo
wfixo1=2*pi*100;
%velocidade angular do sinal sob análise
Vi1=100;
%amplitude do sinal vi1
fase1=-45*pi/180;
%fase do sinal vi1
vi1=100*cos(wfixo1*t+fase1); %vetor sinal vi1
Vo1=Vi1*(cos(fase1)+j*sin(fase1))*(1000./(1000+j*wfixo1)); %cálculo do
amplitude do sinal de saída
vo1=abs(Vo1)*cos(wfixo1*t+angle(Vo1));
%geração do sinal de saída em
função do tempo
plot(t,vo1,t,vi1);
%plote o dois sinais no mesmo
réfico
xlabel('tempo (s)')
ylabel('vo1 e vi1 (V)');
pause
Repetindo o procedimento para o outro componente do sinal.
wfixo2=2*pi*250;
%velocidade angular do sinal sob análise
Vi2=200;
%amplitude do sinal vi2
fase2=30*pi/180;
%fase do sinal vi2
vi2=200*sin(wfixo2*t+fase2); %vetor sinal vi2
Vo2=Vi2*(cos(fase2)+j*sin(fase2))*(1000./(1000+j*wfixo2)); %cálculo do
amplitude do sinal de saída
vo2=abs(Vo2)*cos(wfixo2*t+angle(Vo2));
%geração do sinal de saída em
função do tempo
plot(t,vo2,t,vi2);
%plote os sinais de entrada e saída
xlabel('tempo (s)')
ylabel('vo1 e vi1 (V)');
pause
A tensão resultante na saída é a soma das duas tensões de
saída já obtidas. Assim complemente o SCRIPT:
plot(t, vo1+vo2);
xlabel('tempo (s)')
ylabel('vo1 + vo2 (V)');
2) Repita o procedimento acima para o filtro ativo passa baixas da figura
abaixo
Ri = 1k , Rf= 10k e Cf = 1uF .
3) Repita o procedimento acima para as seguintes funções de transferências: